网络流

模型框架

现实模型：自然水供水系统。它相当于水管调度员。

问题的本质是解决有向图中“资源分配与路径优化”的问题。

定义

两个特殊节点：源点（$S$）、汇点（$T$）。

边的关键属性：容量 $c$。

每条有向边都有一个非负实数“容量”。

性质

“流”作为资源的实际分配，必须满足两个核心规则，否则不是合法的网络流。

容量约束：任意一条边上的实际流量（$f$），不能超过该边的容量（$c$），即 $f \le c$。例如，一根容量为 10 t 的水管，实际输水不能超过 10 t。
流量守恒：除了源点和汇点，其他所有中转节点的“流入流量总和”必须等于“输出流量总和”。
反对称性约束（斜对称）：对任意 $u,v \in V$，$f(u,v) = -f(v,u)$。
弧流量约束（容量限制）：$0 \le f(u,v) \le c(u,v)$。

最大流：流量最大的那个流。

最小割：就是求得一个割 $(S,T)$ 使得割的容量 $c(S,T)$ 最小。

最大流求法

最大流德核心遵循 Ford-Fulkerson 框架：不断在“残留网络”中找“增广路”（能从源点流向汇点且有剩余容量的路径）。
EK 算法适用于节点数 $\le 1000$、边数 $\le 10^4$ 的小规模网络，时间复杂度 $O(F \times E)$（$F$ 是最大流，$E$ 是边数），流量大时效率低。

Dinic 算法：

核心思路

在 Ford-Fulkerson 框架上做两个优化：

分层（BFS）：先给节点按“到源点的最短距离”分层，保证增广路是“最短路径”；
多路增广（DFS）:在分层图中用 DFS 批量找增广路，且用“当前弧优化”避免重复遍历有效边。

大体流程为：

用 bfs 求出 G 中每个点的深度。
用 dfs 在 bfs 所跑出来的途中，枚举一条从源点到汇点的路径 P,求出 $limit = \min{(c \in P)}$，将路径上的每条边都减去 $limit$，并新建一条反边，权值为 $limit$。

当前弧优化

这里的“弧”指的就是一个点 $x$ 向其它点连的有向出边。

当我们选择一个点 $x$ 的第 $i$ 条弧作为一条增广路径的一部分时，前 $i-1$ 条边一定已经能流的都流了，所以考虑标记用到哪条弧，下次 dfs 就可以跳过这些弧，提升程序效率。

复杂度分析

注：不知道严不严谨。（来自 Alex_Wei 的好文）

引理 1

每次增广后的 $S$ 到各个点的最短路不减。

证明

考虑每次加入新边的方向，因为是反向边，所以是从 $dis$ 大的点指向 $dis$ 小的点。

如果最短路长度减少，那么在新的最短路中（记为 $dis'$）一定存在 $(x,y)$ 满足 $dis_x +1 <dis_y$。那么说明 $(x,y)$ 不在原残量网络中，否则不满足三角形不等式（$dis_y \ge dis_x + w$，$w$ 为 $(x,y)$ 的边权）。

由于 $(x,y)$ 是新加入的边，说明 $(y,x)$ 在上一轮被增广，而增广需要满足 $dis_x =dis_y +1$。

于是将 $dis_x = dis_y +1$ 代入 $dis_x + 1 <dis_y$，得到 $dis_y +2 < dis_y$，矛盾，故引理 1 成立。

引理 2

Dinic 的每次增广都会使 $S$ 到 $T$ 的最短路增加。

证明

反证法。设 $S$ 到 $T$ 的最短路不增加。由引理 1 知 $S$ 到 $T$ 的最短路不变。

那么这一条最短路 $P$ 一定不是原残量网络中的最短路（否则会被增广掉），于是必然存在一个 $(x,y)$，满足 $dis_x + 1 < dis_y$（三角不等式在原残量网络上恒成立的逆命题），由类似引理 1 的方法可以导出矛盾，故引理 2 成立。

于是可以得到增广次数是 $O(n)$ 的，因为每次增广都会让增广路上剩余流量最小的边满流（相当于这条边在新图上被删了。这里并不是真正的删掉了，只是因为容量为 $0$ 被跳过不访问，相当于删掉）。我们把这种边称为关键边，一条关键边可以进行一轮增广，所以增广轮数是 $O(m)$ 的，增广路的长度是 $O(n)$。

故 Dinic 的时间复杂度为 $O(n^2m)$，但是这个上界非常松，这也是为什么 Dinic 算法在求网络最大流时表现良好。

模板代码

#include<bits/stdc++.h>
#define int long long
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
using namespace std;

const int INF=1e9; 
const int M=1e5+10,N=1e4+10;
int n,m,S,T,tot=1;
int head[N],del[N],dis[N];

struct edge{
	int to,nxt,w;
}e[M<<2];

void add(int u,int v,int w){
	++tot;
	e[tot].w=w;
	e[tot].to=v;
	e[tot].nxt=head[u];
	head[u]=tot;
}

bool bfs(){
	rep(i,1,n){
		dis[i]=INF;
	}
	queue<int> q;
	dis[S]=0;
	del[S]=head[S];
	q.push(S);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(int i=head[x];i!=0;i=e[i].nxt){
			int y=e[i].to,w=e[i].w;
			if(dis[y]!=INF || w<=0)continue;
			dis[y]=dis[x]+1;
			del[y]=head[y];
			q.push(y);
			if(y==T)return 1; 
		}
	}
	return 0; 
}

int dfs(int x,int limit){
	if(x==T)return limit;
	int flow=0,p;
	for(int i=del[x];i!=0;i=e[i].nxt){
		if(limit<=0)break;
		del[x]=i;
		int y=e[i].to,w=e[i].w;
		if((dis[y]!=dis[x]+1) || w<=0)continue;
		p=dfs(y,min(limit,w));
		if(p==0){
			dis[y]=INF;
			continue;
		}
		e[i].w-=p;
		e[i^1].w+=p;
		flow+=p;
		limit-=p;
	}
	return flow;
}

int dinic(){
	int res=0;
	while(bfs()){
		res+=dfs(S,INF);
	}
	return res;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);cout.tie(nullptr);
	cin>>n>>m>>S>>T;
	while(m--){
		int u,v,c;
		cin>>u>>v>>c;
		add(u,v,c);
		add(v,u,0);
	}
	cout<<dinic()<<"\n";
	return 0;
}

对网络最大流的理解

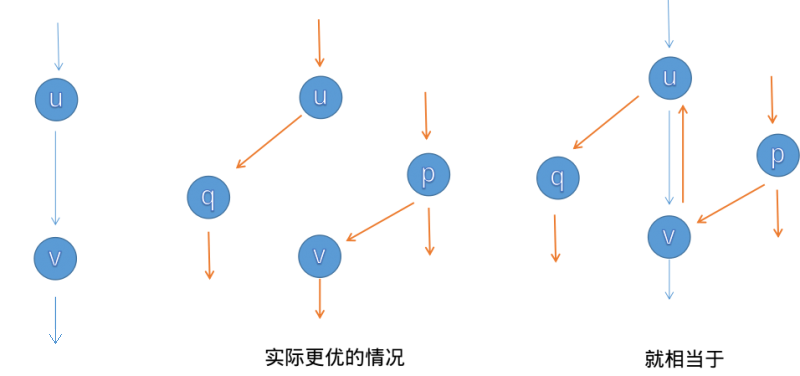
实际上是反悔贪心，我们如果在增广时选择了不是最优的路径去增广，我们可以通过反向边进行反悔。下面是来自 OI-wiki 的一张图：

最小割

多源汇最大流

顾名思义，就是给出若干个源点 $s_i$ 和若干个汇点 $t_i$，求网络的最大流。

考虑图论建模，建出一张新图 $G'$，其中在 $G'$ 的源点 $S$ 向原图 $G$ 中的每个源点连容量为 INF 的边，每个汇点 $t_i$ 向 $G'$ 的汇点 $T$ 连容量为 INF 的边。此时新图的最大流等于原图的最大流。

Proof

证明思想：考虑证明：

对于 $G'$ 中的每一条可行流，都对应着 $G'$ 中的一条可行流。
对于 $G$ 中的每一条可行流，都对应着 $G'$ 中的一条可行流。
于是得到 $G$ 和 $G'$ 中的可行流一一对应，自然就有原图的最大流等于新图的最大流。

对于 $G'$ 中的一条可行流，因为除了 $S,T$ 之外的点都满足流量守恒和容量限制，所以一定对应原图中的一条可行流。
对于 $G$ 中的每一条可行流进行考虑。对于 $G$ 中的点 $v$ 满足 $v \in { V- {s_i,t_i } }$，都满足容量限制和流量守恒。在 $G'$ 中，$S$ 和 $T$ 补偿了原图的源点汇点没有满足流量守恒的情况。（从 $S$ 流出的容量为 INF 的边补偿了 $s_i$ 的入边流量，$T$ 同理），所以 $G'$ 中的每一条可行流也对应着 $G$ 中的一条可行流。

所以 $G'$ 的可行流与 $G$ 的可行流一一对应，由此可得，$G$ 的最大流等于 $G'$ 的最大流。

Code

#include<bits/stdc++.h>
#define int long long
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
using namespace std;

const int INF=1e9; 
const int M=2e5+10,N=5e4+10;
int n,m,S,T,tot=1,Sc,Tc;
int head[N],del[N],dis[N];

struct edge{
	int to,nxt,w;
}e[M<<2];

void add(int u,int v,int w){
	++tot;
	e[tot].w=w;
	e[tot].to=v;
	e[tot].nxt=head[u];
	head[u]=tot;
}

bool bfs(){
	rep(i,0,n+1){
		dis[i]=INF;
	}
	queue<int> q;
	dis[S]=0;
	del[S]=head[S];
	q.push(S);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(int i=head[x];i!=0;i=e[i].nxt){
			int y=e[i].to,w=e[i].w;
			if(dis[y]!=INF || w<=0)continue;
			dis[y]=dis[x]+1;
			del[y]=head[y];
			q.push(y);
			if(y==T)return 1; 
		}
	}
	return 0; 
}

int dfs(int x,int limit){
	if(x==T)return limit;
	int flow=0,p;
	for(int i=del[x];i!=0;i=e[i].nxt){
		if(limit<=0)break;
		del[x]=i;
		int y=e[i].to,w=e[i].w;
		if((dis[y]!=dis[x]+1) || w<=0)continue;
		p=dfs(y,min(limit,w));
		if(p==0){
			dis[y]=INF;
			continue;
		}
		e[i].w-=p;
		e[i^1].w+=p;
		flow+=p;
		limit-=p;
	}
	return flow;
}

int dinic(){
	int res=0;
	while(bfs()){
		res+=dfs(S,INF);
	}
	return res;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);cout.tie(nullptr);
	cin>>n>>m>>Sc>>Tc; 
	S=0,T=n+1;
	while(Sc--){
		int x;
		cin>>x;
		add(S,x,INF);
		add(x,S,0);
	}
	while(Tc--){
		int x;
		cin>>x;
		add(x,T,INF);
		add(T,x,0);
	}
	while(m--){
		int u,v,c;
		cin>>u>>v>>c;
		add(u,v,c);
		add(v,u,0);
	}
	cout<<dinic()<<"\n";
	return 0;
}

参考资料

OI-Wiki。
llr 老师的 PPT。
Acwing 的题解与进阶课。
Alex_Wei 好文。

posted @ 2025-12-10 19:30 lbh666 阅读(2) 评论(0) 收藏举报

刷新页面返回顶部

lbh-juruo

网络流

网络流