CF742B：Arpa’s obvious problem and Mehrdad’s terrible solution（数论）

B. Arpa’s obvious problem and Mehrdad’s terrible solution

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There are some beautiful girls in Arpa’s land as mentioned before.

Once Arpa came up with an obvious problem:

Given an array and a number x, count the number of pairs of indices i, j (1 ≤ i < j ≤ n) such that 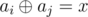, where  is bitwise xoroperation (see notes for explanation).

Immediately, Mehrdad discovered a terrible solution that nobody trusted. Now Arpa needs your help to implement the solution to that problem.

Input

First line contains two integers n and x (1 ≤ n ≤ 105, 0 ≤ x ≤ 105) — the number of elements in the array and the integer x.

Second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 105) — the elements of the array.

Output

Print a single integer: the answer to the problem.

Examples

input

2 3
1 2

output

1

input

6 1
5 1 2 3 4 1

output

2

Note

In the first sample there is only one pair of i = 1 and j = 2.  so the answer is 1.

In the second sample the only two pairs are i = 3, j = 4 (since 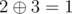) and i = 1, j = 5 (since ).

A bitwise xor takes two bit integers of equal length and performs the logical xor operation on each pair of corresponding bits. The result in each position is 1 if only the first bit is 1 or only the second bit is 1, but will be 0 if both are 0 or both are 1. You can read more about bitwise xor operation here: https://en.wikipedia.org/wiki/Bitwise_operation#XOR.

题意：给n个数字，求有多少对数字异或值为x。

思路：若a^b=c，有a^c=b和b^c=a，于是便容易解决了。

# include <stdio.h>
int a[140000]={0};//数组不要开小了
int main()
{
    int n, x, t;
    long long ans = 0;
    scanf("%d%d",&n,&x);
    while(n--)
    {
        scanf("%d",&t);
        ans += a[x^t];
        ++a[t];
    }
    printf("%I64d\n",ans);
    return 0;
}