红黑树（上）

提到红黑树，就不得不提到AVL树，AVL树又叫做平衡二叉树。这里平衡的意思是指二叉树左右两棵子树的高度之差不会超过1。因此，AVL树是一个最优的二叉排序树，平衡树的树高一直保持在log2N左右。所以每一个操作的时间复杂度都可保持在O(log2N)。但是AVL树在插入和删除节点的时候，为了维持自己的平衡，就不得不调整自己，需要付出相应的代价。

在实际应用中，为了保持二叉排序树的检索性能，我们经常不需要它有那么严格的平衡性，只要保持一种近似的平衡就可以了。工程中，往往使用红黑树，红黑树是一种近似平衡的二叉排序树。

什么是红黑树？

红黑树是每个节点都被染成黑色或者红色的二叉排序树。

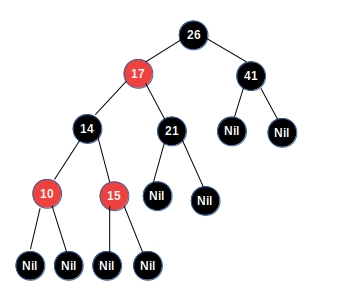
红黑树具有下面5个重要性质：

1. 树中的节点要么是红色要么是黑色
2. 根节点是黑色
3. 每一个叶子节点（Nil，空节点，实际不存储数据）都是黑色的
4. 红色节点的两个孩子都是黑色的
5. 对于每一个节点，从它出发到它的后代叶子节点的所有简单路径上，黑色节点的数量都是相同的

一棵N个节点的红黑树的树高不会超过2log2N，这样红黑树的检索效率仍然是对数级别的。

性质1、2、3比较容易理解，性质4保证了红黑树的树高不会相差太大，性质5保证了红黑树树高的相对平衡性。这其中，红色节点 起到了调节的作用，能够让红黑树在不那么平衡的情况下，仍保证黑色节点的数量，同时又保证了红色节点不会泛滥，树上的性能不会被破坏。

为了维持这5条性质，红黑树在插入和删除节点需要做相应的调整。

红黑树的插入操作

红黑树也是一种二叉排序树，所以向一棵红黑树中插入节点的步骤和二叉排序树都是相同的，都是找到正确的位置，并新建节点插入。我们需要注意的是，在插入一个节点的时候，在什么情况下，有哪些红黑树的性质会被打破，我们应该怎么把红黑树调整回来。

我们以插入节点Z为例。对于这个新的Z节点，首先要设置它的颜色为红色。因为如果设置为黑色，就会直接打破性质5，调整起来比较麻烦。在插入红色节点Z之后，我们重新来看红黑树的5条性质。首先，性质1和3是完全不会被打破的。由于Z节点的初始颜色是红色，而插入取代的位置一定是黑色的Nil节点，同时Z自己也会有2个黑色的Nil节点。所以在插入节点Z之后，Z所在的路径上减少了1个黑色节点，增加了1个红色节点，同时Z节点下面的2条路径各增加一个黑色的节点，性质5同样不会被打破。

性质2和性质4是可能被打破的。

首先来看性质2，性质2被打破的唯一一种情况是：我们插入的位置就是根节点，这种情况下，我们插入的是一棵空树，我们直接把Z节点的颜色变成黑色就可以了，改变颜色也不会影响性质5。

性质4被打破的情况，就是我们插入的节点Z在一个红色节点的下面，这个时候，可以根据Z节点叔叔的颜色分成3种情况：

1. Z节点的叔叔是红色节点
2. Z节点是其父亲的左子节点，Z节点的叔叔是黑色节点
3. Z节点是其父亲的右子节点，Z节点的叔叔是黑色节点

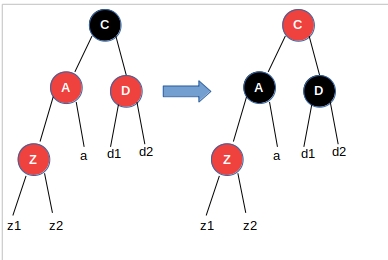
第1种情况：Z节点的叔叔是红色节点

这里的Z节点可能是刚刚插入的新节点，也可能是第1种情况调整之后的C节点，如果是刚刚插入的新节点，那么z1、z2、a、d1、d2就是Nil黑色节点，如果是第1种情况调整之后的C节点，那么z1、z2、a、d1、d2就是树阶（路径上黑色节点数量）相同的子树，但是这些都不影响我们的调整策略。当前来看，性质5保持住了，但是性质4破坏了，为了修复性质4，我们可以把节点A和节点D变成黑色节点，然后把节点C变成红色，这样C以下的就调整完了。但是还没有结束，C的颜色改变可能导致C和它的父节点不符合红黑树的定义。比如C本来是根节点，现在变成红色节点了；又或者C的父亲是红色节点，现在C也是红色节点。我们需要进一步调整，其实C本来是根节点的话，直接把C变成黑色就解决问题了。C的父亲是红色节点的情况，需要继续根据依据第1、2、3种情况调整。C的父亲是黑色节点，没有影响，依然是一棵符合定义的红黑树。注意，这里的Z节点是A的左节点还是右节点都没有关系，都是一样的调整策略。

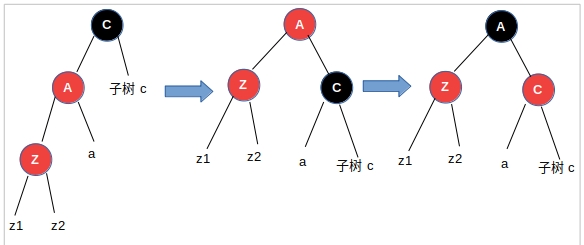
第2种情况：Z节点是其父亲的左子节点，Z节点的叔叔是黑色节点

这里的Z节点可能是刚刚插入的新节点，也可能是第1种情况调整之后的C节点，如果是刚刚插入的新节点，那么z1、z2、a、子树c就是Nil黑色节点，如果是第1种情况调整之后的C节点，那么z1、z2、a、子树c就是树阶相同的子树，并且子树c是以黑色节点为根节点的子树，但是这些都不影响我们的调整策略，调整的步骤都是一样的。对C节点进行右旋，让C变成A的右子节点，子树a变成C的左子节点，A顶替原来C的位置，然后再把A的颜色变成黑色，C的颜色变成红色，满足性质5，调整结束。

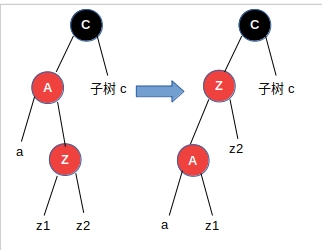
第3种情况：Z节点是其父亲的右子节点，Z节点的叔叔是黑色节点

这里的Z节点可能是刚刚插入的新节点，也可能是第1种情况调整之后的C节点，如果是刚刚插入的新节点，那么z1、z2、a、子树c就是Nil黑色节点，如果是第1种情况调整之后的C节点，那么z1、z2、a、子树c就是树阶相同的子树，并且子树c是以黑色节点为根节点的子树，但是这些都不影响我们的调整策略，调整的步骤都是一样的。我们可以想办法把情况3转化成情况2，然后根据情况2进行调整就可以了。我们对A节点进行左旋，把A节点变成Z节点的左节点，Z节点顶替之前A节点的位置。这样就是我们熟悉的情况2了，但是把A节点当做情况2中的Z节点进行处理就可以了。

 

上面3种情况只考虑了Z的父节点是祖父节点的左节点的情况，对于右节点的情况，对称考虑进行调整就可以了。调整策略如下：

• Z节点的叔叔是红色节点

节点A、D由红变黑，节点C由黑变红

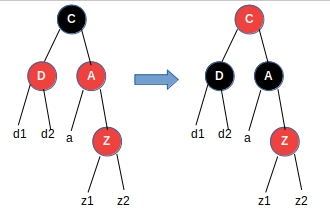
• Z节点是其父亲的右子节点，Z节点的叔叔是黑色节点

节点C左旋，节点C由黑变红，节点A由红变黑

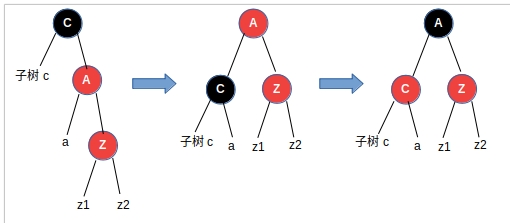
• Z节点是其父亲的左子节点，Z节点的叔叔是黑色节点

节点A右旋，然后再根据第2种情况调整

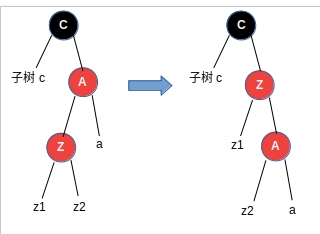
 红黑树的删除操作情况更加复杂，有时间再写写。红黑树的插入操作实现代码，可以参考 https://gitee.com/liuanyou/redblacktree