LeetCode不同路径 动态规划

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

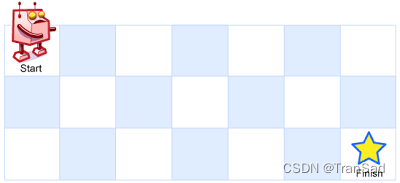
输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下

2. 向下 -> 向下 -> 向右

3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

思路：

  我对这个题印象很深刻，因为在大二上算法课程时接触过，当时老师画了一个类似这样的二维图，让我们求到达某处时的路径数……当时还确实是傻傻的去数路径数目，还妄想从数个数的角度总结规律。

  直接说重点：这个题要用动态规划的方式。我们知道，机器人只能向下走或者向右走，因此对于到达每一个位置的路径数，等于到达它上面位置的路径数+到达它左边位置的路径数。

  我们定义一个二维的动态规划数组dp[][]，dp[i][j]表示到达(i,j)位置的路径数。

  状态转移方程就是：

    dp[i][j] = dp[i-1][j]+dp[i][j-1]

  对于最上边和最左边的位置，到达他们的路径只有一条，所以他们其实都是1。当然这也同样符合我们的状态转移方程——比如对于最上面的网格dp[i][0]，因为dp[i][0-1]是不存在的，所以dp[i][0]=dp[i-1][0]+0,即dp[i][0]=dp[i-1][0]。

代码：

class Solution(object):

    def uniquePaths(self, m, n):

        dp = [[0]*n for _ in range(m)]#初始化动态规划数组，与原网格同样大小

        for i in range(n):#初始化最上面的一行为1

            dp[0][i]=1

        for j in range(m):#初始化最左边的一列为1

            dp[j][0]=1

        #开始动态规划

        for i in range(1,m):#对于非最上边和非最左边的网格，使用状态转移方程

            for j in range(1,n):

                dp[i][j] = dp[i-1][j]+dp[i][j-1]

        return dp[m-1][n-1]#返回到达右下角的路径数

小结：

  开篇我已经提到，这道题是动态规划的经典到不能再经典的题。包括今年（2021年）我参加过网易的秋招笔试时，我记得第四道题就是类似这样可以用动态规划解决的路径问题，甚至就几乎是62或64题原题！因此请一定要掌握哈。

  这道题和64. 最小路径和极其相关，强烈建议对比学习，共同掌握，在对比中你会豁然开朗！