平衡二叉树

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

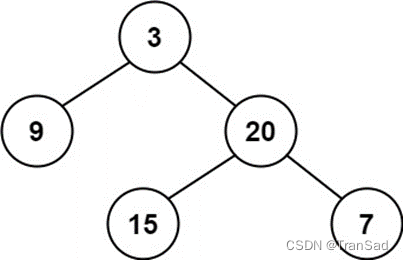
输入：root = [3,9,20,null,null,15,7]

输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]

输出：false

示例 3：

输入：root = []

输出：true

思路：

  根据题意，要是平衡二叉树，每一个节点的左右子树的深度差不能超过1。因此如果我们用递归来解决的话，对于当前节点，我们得到它左右子树的深度后进行判断，如果当前节点的左右子树深度差合法，那么就继续递归它的左节点和右节点。

  那么如何获得左右子树的深度呢？也还是用递归解决，我们做过求二叉树深度的那一题，一个两行的递归函数就可以搞定。

代码：

class Solution(object):

    def isBalanced(self, root):

        def depth(root):#获取二叉树的深度

            if not root:return 0

            return max(depth(root.left),depth(root.right))+1

        def is_avl(root):

            if not root:return True#如果遍历到底，则返回True

           #如果左右高度差小于1

            if depth(root.left)-depth(root.right)<-1 or depth(root.left)-depth(root.right)>1:

                return False#则不满足条件 返回False

            else:#当前节点满足了，继续递归到它的左右子节点

                return (is_avl(root.left) and is_avl(root.right))

        return is_avl(root)

小结：

  从递归最外层来看，对于根节点root，如果它自己的左右子树深度差不超过1，且它的左右子节点各自也满足这个条件，那么这棵树就是一个平衡二叉树，不需要跳进递归里去。 

  这个解法里有两个递归（求深度也用了递归），所以效率并不高。只不过它符合最传统的递归解决方式，只要按照之前做二叉树的思路部就班地写出递归函数来就可以解决。