Matlab分析S参数

1、读取单端S4P并绘制图形

filename = 'TX1_RX1.s4p';
backplane = sparameters(filename);  %读入S4P文件
data = backplane.Parameters;         %S矩阵数据读取定义
freq = backplane.Frequencies;        %频点读取定义
z0 = backplane.Impedance;             %特征阻抗读取定义

% IQS参数
s11_iq = squeeze(data(1,1,:));  % S11
s12_iq = squeeze(data(1,2,:));  % S12
s13_iq = squeeze(data(1,3,:));  % S13
s14_iq = squeeze(data(1,4,:));  % S14

s21_iq = squeeze(data(2,1,:));  % S21
s22_iq = squeeze(data(2,2,:));  % S22
s23_iq = squeeze(data(2,3,:));  % S23
s24_iq = squeeze(data(2,4,:));  % S24

s31_iq = squeeze(data(3,1,:));  % S31
s32_iq = squeeze(data(3,2,:));  % S32
s33_iq = squeeze(data(3,3,:));  % S33
s34_iq = squeeze(data(3,4,:));  % S34

s41_iq = squeeze(data(4,1,:));  % S41
s42_iq = squeeze(data(4,2,:));  % S42
s43_iq = squeeze(data(4,3,:));  % S43
s44_iq = squeeze(data(4,4,:));  % S44

% 单端S参数
s11 = 20*log10(abs(s11_iq));  
s12 = 20*log10(abs(s12_iq));  
s13 = 20*log10(abs(s13_iq));  
s14 = 20*log10(abs(s14_iq));  

s21 = 20*log10(abs(s21_iq));
s22 = 20*log10(abs(s22_iq));
s23 = 20*log10(abs(s23_iq));
s24 = 20*log10(abs(s24_iq));

s31 = 20*log10(abs(s31_iq));
s32 = 20*log10(abs(s32_iq));
s33 = 20*log10(abs(s33_iq));
s34 = 20*log10(abs(s34_iq));

s41 = 20*log10(abs(s41_iq));
s42 = 20*log10(abs(s42_iq));
s43 = 20*log10(abs(s43_iq));
s44 = 20*log10(abs(s44_iq));

% 绘制幅度响应曲线
figure;
% subplot(1,1,1);
semilogx(freq/1e9, s11, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, s12, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s13, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s14, 'm', 'LineWidth', 1.5);

semilogx(freq/1e9, s21, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s22, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s23, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s24, 'm', 'LineWidth', 1.5);

semilogx(freq/1e9, s31, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s32, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s33, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s34, 'm', 'LineWidth', 1.5);

semilogx(freq/1e9, s41, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s42, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s43, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s44, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
title('SE S-Parameters Magnitude');

2、单端S4P转平衡端口（BAL-BAL）并绘制图形

% SE转BAL-BAL
diffdata = s2sdd(data);  %使用s2sdd函数提取差分S参数，13,24
diffz0 = 2*z0;

diffsparams = sparameters(diffdata,freq,diffz0)
% rfwrite(diffdata, freq, 'diffspara_1.s2p')  %写出新的S2P文件

% 提取差分S参数的各个分量
sdd11 = squeeze(diffdata(1,1,:));  % SDD11
sdd21 = squeeze(diffdata(2,1,:));  % SDD21
sdd12 = squeeze(diffdata(1,2,:));  % SDD12
sdd22 = squeeze(diffdata(2,2,:));  % SDD22

% 转换为dB单位
sdd11_dB = 20*log10(abs(sdd11));
sdd21_dB = 20*log10(abs(sdd21));
sdd12_dB = 20*log10(abs(sdd12));
sdd22_dB = 20*log10(abs(sdd22));

% 绘制幅度响应曲线
figure;
subplot(1,1,1);
semilogx(freq/1e9, sdd11_dB, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, sdd21_dB, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd12_dB, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd22_dB, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
title('Differential S-Parameters Magnitude');
legend('SDD11', 'SDD21', 'SDD12', 'SDD22', 'Location', 'best');

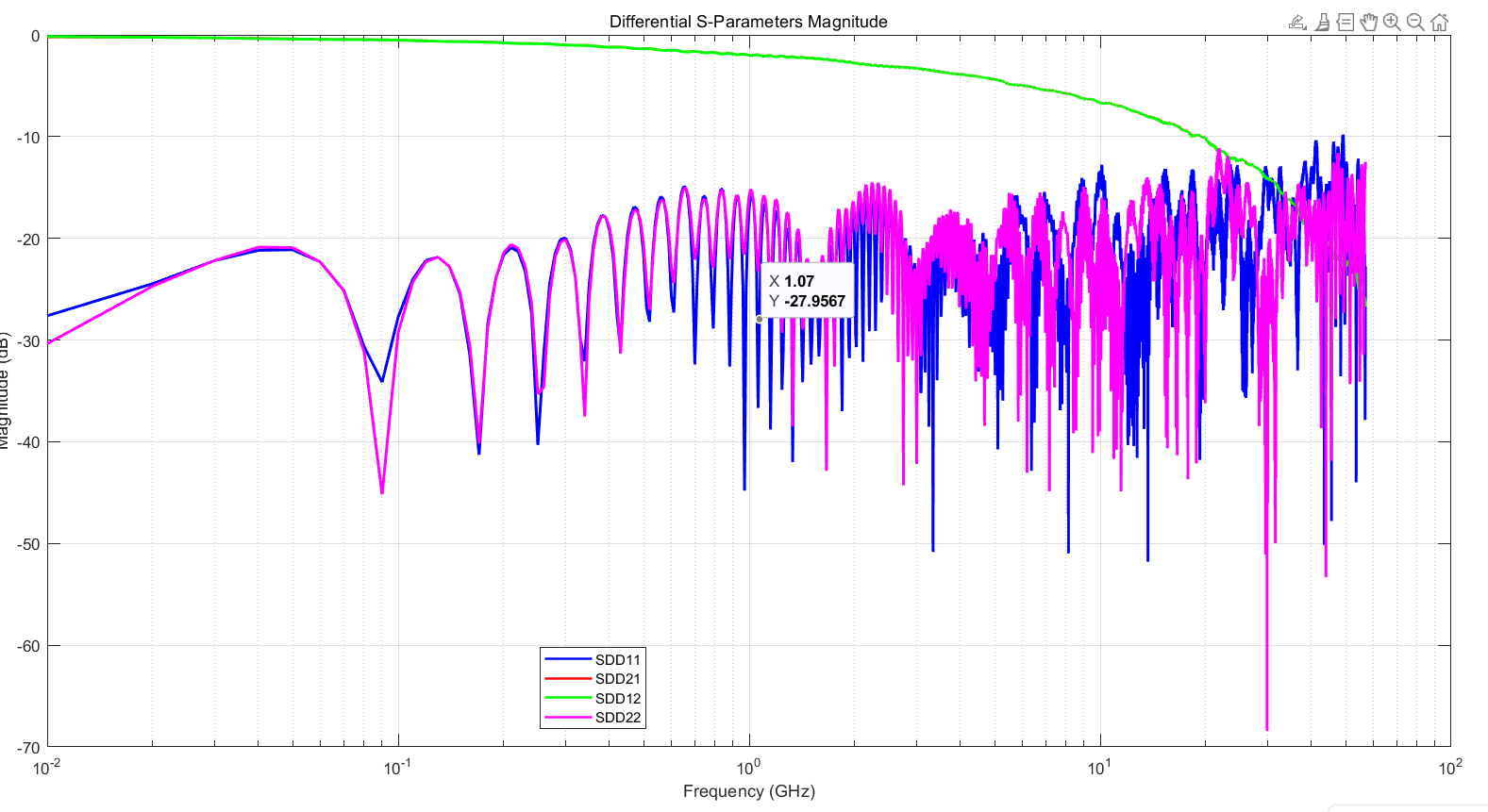
除了SDD外，其他差分、共模S参数转换函数参考：

 s2sdd - Convert 4-port, single-ended S-parameters to 2-port, differential-mode S-parameters (Sdd) - MATLAB

 

3、单端S32P转单端S4P再转平衡端口（BAL-BAL）并绘制图形

filename = 'DUT1_1kHz.s32p';
backplane = sparameters(filename)
freq = backplane.Frequencies;
n2m = [1 17 2 18];   %差分端口设定
z0 = backplane.Impedance;
first4portdata = snp2smp(backplane.Parameters,z0,n2m,z0);
first4portsparams = sparameters(first4portdata,freq,z0)
diffdata = s2sdd(first4portdata) %提取这一对的差分S参数
% rfwrite(diffdata, freq, 'diffspara.s2p') %导出新的S参数

% 提取差分S参数的各个分量
sdd11 = squeeze(diffdata(1,1,:));  % SDD11
sdd21 = squeeze(diffdata(2,1,:));  % SDD21
sdd12 = squeeze(diffdata(1,2,:));  % SDD12
sdd22 = squeeze(diffdata(2,2,:));  % SDD22

% 转换为dB单位
sdd11_dB = 20*log10(abs(sdd11));
sdd21_dB = 20*log10(abs(sdd21));
sdd12_dB = 20*log10(abs(sdd12));
sdd22_dB = 20*log10(abs(sdd22));

% 绘制幅度响应曲线
figure;
subplot(1,1,1);
semilogx(freq/1e9, sdd11_dB, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, sdd21_dB, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd12_dB, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd22_dB, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
title('Differential S-Parameters Magnitude');
legend('SDD11', 'SDD21', 'SDD12', 'SDD22', 'Location', 'best');

 

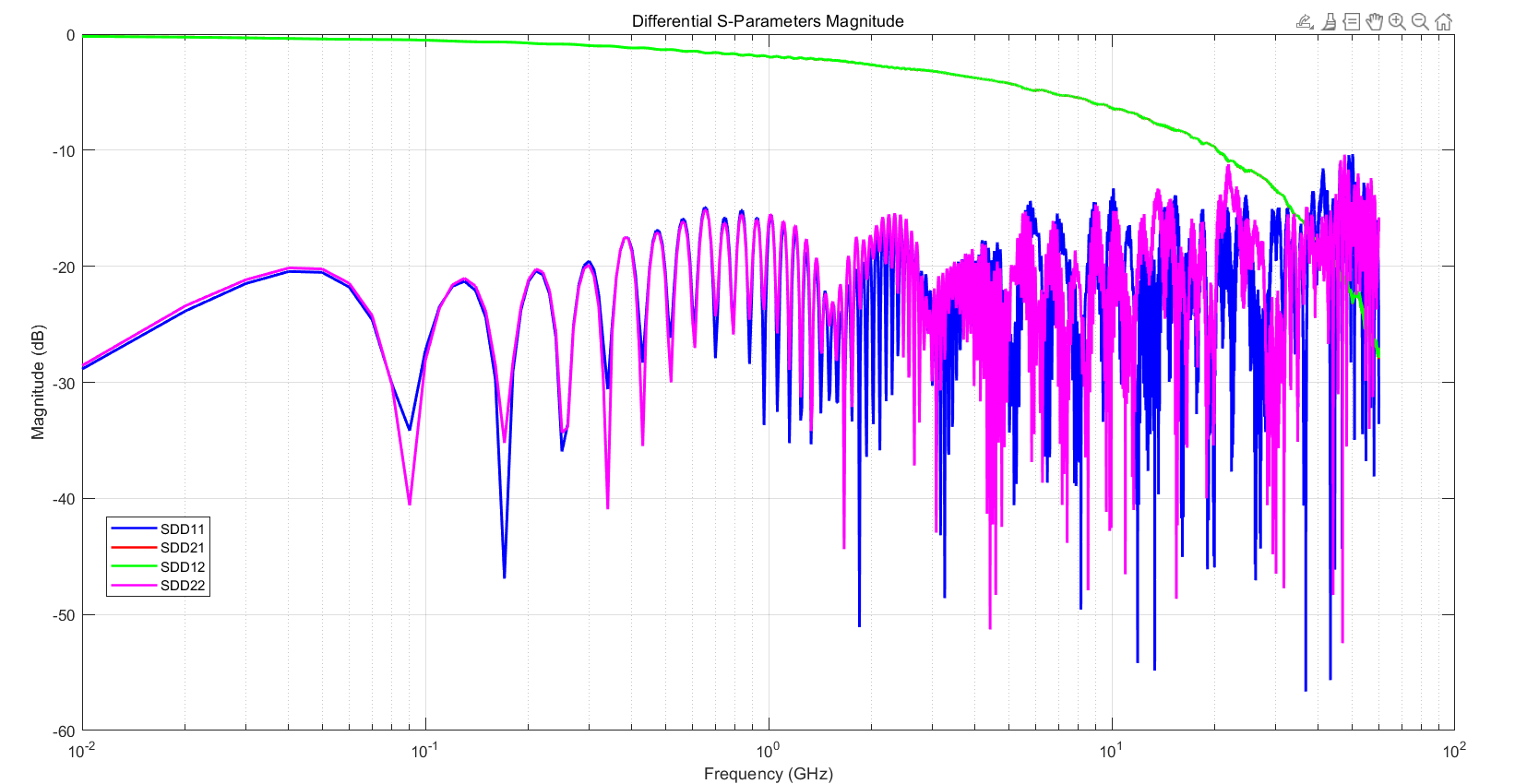
参考：如何使用MATLAB对S参数进行后处理 - MATLAB & Simulink