德育未来集训笔记-Day 5-KMP

KMP 算法

算法简介

KMP（Knuth-Morris-Pratt）算法是一种高效的字符串模式匹配算法，用于在一个文本串（Text）中快速查找一个模式串（Pattern）的所有出现位置。
主要特点是通过预处理模式串构建 next 数组（部分匹配表），避免匹配失败时文本串指针的回退，将暴力匹配的 \(O(n*m)\) 时间复杂度优化至 \(O(n+m)\)（\(n\) 为文本串长度，\(m\) 为模式串长度）。
KMP 算法能在单次遍历文本串的过程中完成匹配，尤其适合模式串较长、需要多次匹配的场景，效率远高于暴力匹配。

基本思想

其基本思想是，利用模式串自身的前后缀重复信息，构建 next 数组记录“最长相等前后缀长度”，当匹配失败时，仅回退模式串指针到 next 数组指定的位置，而非回退文本串指针。

• 前缀：模式串中除最后一个字符外，以第一个字符开头的连续子串（如 abcab 的前缀为 a、ab、abc、abca）；
• 后缀：模式串中除第一个字符外，以最后一个字符结尾的连续子串（如 abcab 的后缀为 b、ab、cab、bcab）；
• next[i]：模式串前 \(i+1\) 个字符组成的子串中，最长相等前缀和后缀的长度（特殊值 -1 表示无相等前后缀）。
  KMP 算法先通过 next 数组预处理模式串，再用预处理结果指导文本串的匹配过程，核心是“利用已匹配的信息，避免重复比较”。

操作步骤

关于最长相等前后缀长度，请见picture1.jpg

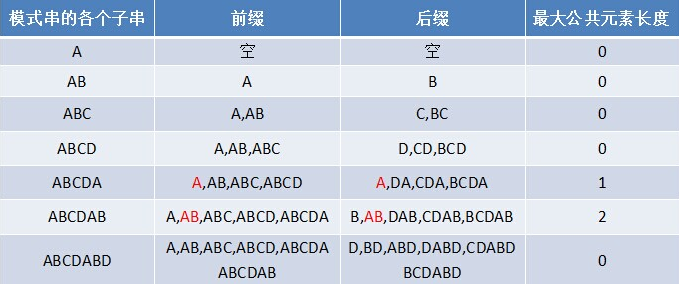
步骤 1：预处理模式串，构建 next 数组

定义 next 数组：

• next 数组长度与模式串长度一致，next[i] 表示模式串前 \(i+1\) 个字符的最长相等前后缀长度（边界值 next[0] = -1）。

构建规则：

1. 初始化指针：i = 0（模式串主指针，遍历模式串），j = -1（前后缀匹配指针，初始为边界）；
2. 循环遍历模式串（直到 \(i < m-1\)，\(m\) 为模式串长度）：
   • 若 \(j = -1\)（边界）或模式串 pattern[i] == pattern[j]：
     \(i++\)，\(j++\)，next[i] = j（记录当前位置的最长相等前后缀长度）；
   • 否则：\(j = next[j]\)（回退前后缀指针，避免重复比较）。

步骤 2：文本串与模式串的匹配过程

定义两个指针：

• \(i\)：文本串指针（初始为 0，仅向前移动，不回退）；
• \(j\)：模式串指针（初始为 0，匹配失败时通过 next 数组回退）。

匹配规则：

1. 循环遍历文本串（直到 \(i < n\)，\(n\) 为文本串长度）：
   • 若 \(j = -1\)（边界）或文本串 text[i] == pattern[j]：
     \(i++\)，\(j++\)（同时向前移动指针，继续匹配）；
   • 否则：\(j = next[j]\)（仅回退模式串指针，文本串指针不动）；
   • 若 \(j == m\)（模式串完全匹配）：
     记录匹配起始位置（\(i - j\)）；
     \(j = next[j-1]\)（回退模式串指针，支持重叠匹配），\(i--\)（文本串指针回退，避免跳过字符）。

步骤 3：输出结果

输出所有匹配的起始位置，或统计匹配次数、判断是否包含模式串等。

例1

【题目描述】

输入一个文本串和一个模式串，求出模式串在文本串中的所有匹配起始位置；若未匹配到，输出 -1。

【输入】

第一行输入文本串（长度不超过 \(10^5\)）；
第二行输入模式串（长度不超过 \(10^4\)）。

【输出】

第一行输出匹配次数；
第二行输出所有匹配的起始位置（用空格分隔），若无匹配则输出 -1。

【输入样例】

ababababxabcabab
abab

【输出样例】

4
0 2 4 11

【提示】

对于全部数据，文本串长度 \(\le 10^5\)，模式串长度 \(\le 10^4\)，字符仅包含大小写字母、数字。

答案

以下答案KMP结构体部分选自jtbg.h内部版 第\(6556\)至\(6668\)行

#include <bits/stdc++.h>
using namespace std;
struct kmp 
{
private:
	string pattern;
	vector<int> next;
	void buildNext()
	{
		int m = pattern.length();
		next.resize(m, 0);
		next[0] = -1;
		int i = 0, j = -1;
		while (i < m - 1) 
		{
			if (j == -1 || pattern[i] == pattern[j]) 
			{
				i++;
				j++;
				next[i] = j;
			} 
			else
			{
				j = next[j];
			}
		}
	}
	
public:
	kmp(const string& pat="") : pattern(pat) 
	{
		buildNext();
	}
	
	void reset(const string& p)
	{
		pattern=p;
		next.clear();
		buildNext();
	}
	
	// 搜索所有匹配位置
	vector<int> search(const string& text) 
	{
		vector<int> result;
		int n = text.length();
		int m = pattern.length();
		
		if (m == 0) return result;
		
		int i = 0, j = 0;
		while (i < n) {
			if (j == -1 || text[i] == pattern[j]) 
			{
				i++;
				j++;
			} 
			else 
			{
				j = next[j];
			}
			
			if (j == m) 
			{
				result.push_back(i - j);
				j = next[j - 1];  // 继续搜索
				i--;  // 回退一步
			}
		}
		return result;
	}
	
	// 搜索第一个匹配位置，返回-1表示未找到
	int findFirst(const string& text) 
	{
		int n = text.length();
		int m = pattern.length();
		
		if (m == 0) return 0;
		
		int i = 0, j = 0;
		while (i < n && j < m) 
		{
			if (j == -1 || text[i] == pattern[j]) 
			{
				i++;
				j++;
			} 
			else 
			{
				j = next[j];
			}
		}
		
		return (j == m) ? (i - j) : -1;
	}
	
	// 判断是否包含模式串
	bool contains(const string& text) 
	{
		return findFirst(text) != -1;
	}
	
	// 获取next数组（用于调试）
	vector<int> getNext() const 
	{
		return next;
	}
	
	// 统计匹配次数
	int count(const string& text) 
	{
		return search(text).size();
	}
};
int main() 
{
    string text, pattern;
    getline(cin, text);   // 读取文本串（支持含空格）
    getline(cin, pattern);// 读取模式串（支持含空格）

    // 初始化KMP对象
    kmp kmp_obj(pattern);

    // 获取匹配结果
    vector<int> matchPos = kmp_obj.search(text);
    int matchCount = matchPos.size();
    cout << matchCount << endl;
    if (matchCount == 0) 
	{
        cout << -1 << endl;
    } 
	else 
	{
        for (size_t i = 0; i < matchPos.size(); i++) 
		{
            if (i > 0) cout << " ";
            cout << matchPos[i];
        }
        cout << endl;
    }

    return 0;
}