德育未来集训笔记-Day 1-Dijkstra

Dijkstra 迪杰斯特拉

算法简介

Dijkstra (迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。

基本思想

其基本思想是，设置顶点集合S和U并不断地作贪心选择来扩充S这个集合。
一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时，S中仅含有原点(出发点)，U中有除原点外的点。
设k是U的某一个顶点，把从原点到k且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组记录当前每个顶点所对应的最短特殊路径长度。
Dijkstra算法每次从U中取出具有最短特殊路长度的顶点k，将k添加到S中，同时对数组dist作必要的修改。
一旦S包含了所有U中顶点，也就是说U中没有顶点，即已知所有顶点到原点的最短路径，dist就是从源到所有其它顶点之间的最短路径长度。

操作步骤

步骤 1：初始化基础数据结构
定义两个集合：

• S（已确定最短路径的顶点集合）：初始时仅包含源点（出发点）。
• U（未确定最短路径的顶点集合）：初始时包含除源点外的所有顶点。

定义一个距离数组 \(dist\)：
\(dist_i\) 表示从原点到顶点 \(i\) 的当前最短特殊路径长度（仅经过 S 中顶点的路径）。
初始化规则：原点到自身的距离为 \(0\)（\(dist_{原点} = 0\)）；原点直接相连的顶点距离为对应边的权重；无直接相连的顶点距离为无穷大（\(∞\)）。

定义一个前驱数组 \(prev\)（可选，用于回溯最短路径）：记录每个顶点在最短路径上的前一个顶点，初始时所有顶点的前驱为-1（无）。

步骤 2：核心循环（扩充 S 集合）
循环执行以下操作，直到\(U\)为空（所有顶点都加入\(S\)）：

• 贪心选择：从\(U\)中找到\(dist\)值最小的顶点\(k\)（即当前最短特殊路径的终点）。
• 扩充 \(S\) 集合：将顶点\(k\)从\(U\)移除，加入\(S\)。
• 松弛操作：对所有仍在\(U\)中的顶点\(v\)，检查 “原点->k->v” 的路径长度是否比当前\(dist_v\)更小：
• 若 \(dist_k\) + 边\((k,v)\)的权重 \(<\) \(dist_v\)，则更新 \(dist_v\) \(=\) \(dist_k\) + 边\((k,v)\)的权重，并更新\(prev_v = k\)。

步骤 3：输出结果
\(dist\) 数组即为原点到所有顶点的最短路径长度。
若需要具体路径，可通过\(prev\)数组回溯（如从目标顶点倒推回原点）。

例1

【题目描述】

输入一个图，求出原点到各个点之间的距离。

【输入】

第一行两个整数 \(N\),\(M\) 表示顶点的个数和原点编号；

每 \(1+y\) 行为 \(2\) 个数:

• 接下来一行两个数 \(x\),\(y\) ,表示顶点编号和这个顶点链接的边数。
• 接下来y行两个数 \(a\),\(b\) ,表示\(x\)号顶点有一条边链接\(a\)号顶点和这个边的长度(权重)。

【输出】

输出共 \(N\) 行，每行输出两个数，用:号隔开，表示顶点编号和从原点到这个顶点的距离。

【输入样例】

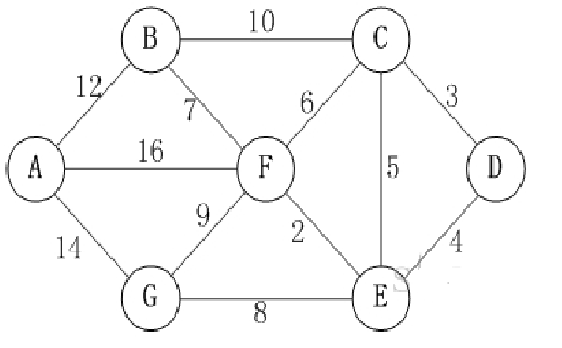
(以下输入样例的图见picture1.jpg)
picture1.jpg

7 
1 
1 2 
2 3 
3 4 
2 4 
7 10 
4 6 
3 5 
1 3 
3 4 
1 4 
2 5 
4 2 
5 8 
4 5 
7 7 
2 6 
3 2 
5 9  
6 16 
5 3 
6 14 
4 9 
3 8 
6 3 
7 12 
4 16 
5 14 
7 3 
6 12 
2 10 
4 7 

【输出样例】

1:0 
2:3 
3:4 
4:6 
5:12 
6:22 
7:13 

【提示】

对于全部数据，\(1\le N\le 2.5\times10^2\)。数字不超过 C/C++ 的 int 范围。

答案

#include <bits/stdc++.h>
using namespace std;

const int N = 250;       // 最大顶点数
const int INF = 0x3f3f3f3f; // 表示无穷大（避免溢出）
int q[N][N];             // 邻接矩阵，q[i][j]表示i到j的边权，INF表示无连接
int dist[N];             // dist[i]：源点到i的最短路径长度
bool visited[N];         // visited[i]：是否已确定i的最短路径（对应集合S）
int n,st;               // n：顶点数，st：源点

int main() 
{
	// 1. 初始化邻接矩阵为无穷大（无连接）
	memset(q, 0x3f, sizeof(q));
	for (int i = 1; i <= N; i++) q[i][i] = 0; // 自身到自身的距离为0
	
	// 2. 输入顶点数和源点
	cin >> n >> st;
	
	// 3. 输入边的信息（格式：起点 边数 终点1 权值1 终点2 权值2 ...）
	for (int i = 1; i <= n; i++) 
	{
		int x, y;
		cin >> x >> y; // x：当前顶点，y：x的出边数
		while (y--) 
		{
			int a, b;
			cin >> a >> b; // a：邻接顶点，b：边权
			q[x][a] = b;   // 无向图，双向赋值
			q[a][x] = b;
		}
	}
	
	// 4. Dijkstra算法初始化
	memset(dist, 0x3f, sizeof(dist)); // 初始距离均为无穷大
	dist[st] = 0;                     // 源点到自身的距离为0
	memset(visited, false, sizeof(visited)); // 初始所有顶点未访问（不在S中）
	
	// 5. 核心循环：遍历n次，确定n个顶点的最短路径
	for (int i = 1; i <= n; i++)
	{
		// 5.1 找到未访问的、dist最小的顶点u
		int u = -1;
		int min_dist = INF;
		for (int j = 1; j <= n; j++) 
		{
			if (!visited[j] && dist[j] < min_dist) 
			{
				min_dist = dist[j];
				u = j;
			}
		}
		
		if (u == -1) break; // 剩余顶点不可达，提前退出
		visited[u] = true;  // 将u加入集合S（标记为已确定）
		
		// 5.2 松弛操作：更新u的邻接顶点的dist
		for (int v = 1; v <= n; v++)
		{
			// 仅更新未访问的顶点，且u到v有边，且经过u的路径更短
			if (!visited[v] && q[u][v] != INF) 
			{
				if (dist[v] > dist[u] + q[u][v]) 
				{
					dist[v] = dist[u] + q[u][v];
				}
			}
		}
	}
	
	// 6. 输出结果：源点到每个顶点的最短路径长度
	for (int i = 1; i <= n; i++) 
	{
		cout << i << ":";
		if (dist[i] == INF) 
		{
			cout << "NaN" << endl;//不可到达
		} 
		else
		{
			cout << dist[i] << endl;
		}
	}
	
	return 0;
}