12. 寻找环形链表的头结点

题目描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

题目链接

https://leetcode-cn.com/problems/linked-list-cycle-ii/

示例

示例1：

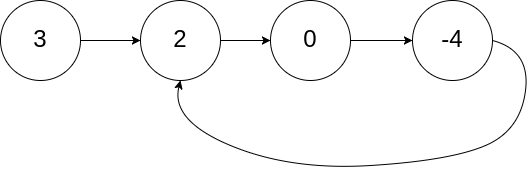
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例2：

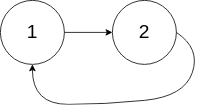
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

解法一

思路

遍历链表中的每个结点，将它记录下来，一旦遇到了此前遍历过的结点，可以盘点该节点为环的起点

复杂度分析

n为链表中的结点
时间复杂度分析：
O(n)：我们需要将链表中的所有结点都访问一次。
空间复杂度分析：
O(n)：我们需要及那个链表中的每个结点都保存在哈希表当中。

代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode n = head;
        Set<ListNode> set = new HashSet<>();
        while (n != null) {
            if (set.contains(n)) {
                return n;
            } else {
                set.add(n);
            }
            n = n.next;
        }
 
        // 如果没有重复加入的结点，就返回null
        return null;
    }
}

解法二

思路

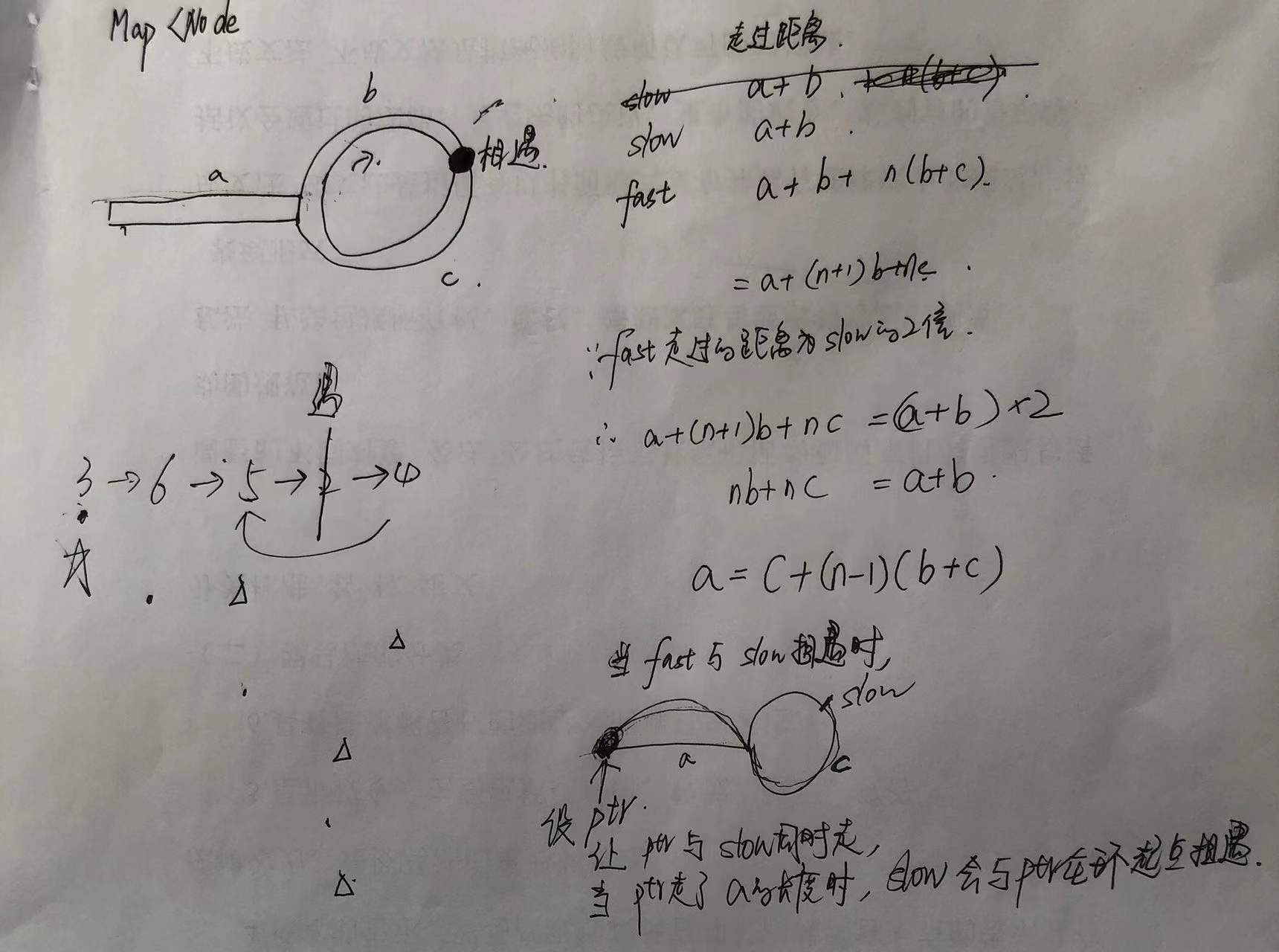
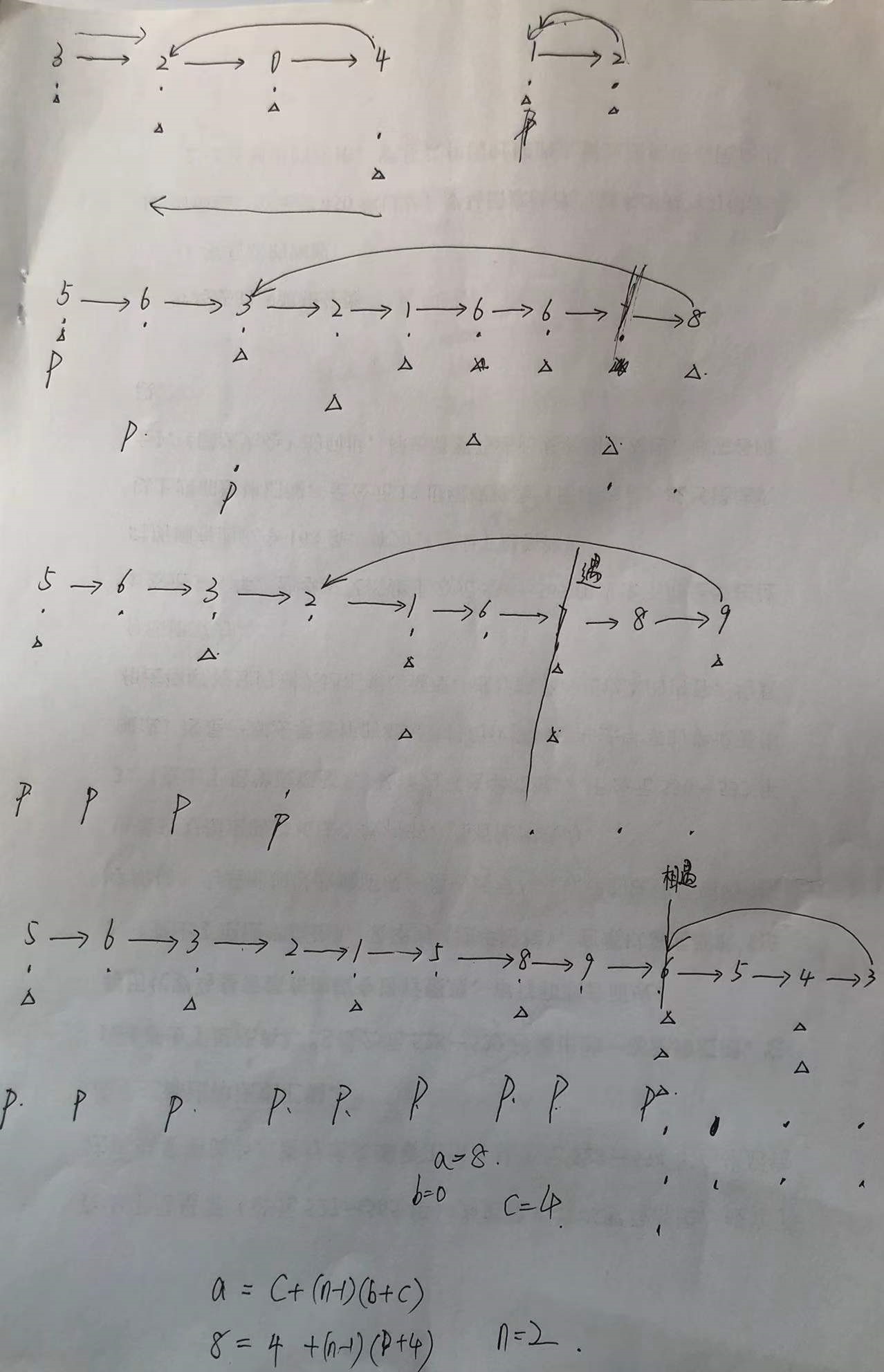
复杂度分析

时间复杂度分析：
在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(N)+O(N)=O(N)。
空间复杂度分析：
O(1)。我们只使用了三个指针。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
 
        while (true) {
            if (fast == NULL || fast->next == NULL) {
                return NULL;
            }
 
            slow = slow->next;
            fast = fast->next->next;
 
            if (slow == fast) {
                break;
            }
        }
 
        ListNode* p = head;
        while (p != slow) {
            p = p->next;
            slow = slow->next;
        }
        return p;
    }
};