理论物理极础2. 运动

莱尼抱怨：“乔治，跳跃频闪的东西令我不爽。时间是蹦蹦跳跳而溜去的吗？我希望事情平滑而行。”乔治思考片刻，擦掉黑板，“好的，莱尼，今天我们就学习平滑变化的系统。”

插播数学：微分

在本书中，我们主要处理的问题是，看物理量如何随时间变化。经典力学主要研究事物如何平滑变化，用数学中的术语就是连续变化。状态将依据动力学定律随时间演化连续更新，不同于上一节中的频闪变化。因此，我们有兴趣学学独立变量\(t\)的函数。

数学上处理连续变化需要用微分。微分与极限密切相关，我们先讨论下极限。我们考虑一个数列\(l_1\), \(l_2\), \(l_3\), \(\ldots\), 它们越来越靠近某个值\(L\)，\(L\)即成为数列的极限。比如数列：0.9, 0.99, 0.999, 0.9999, . . . ，这个数列的极限为1。数列里没有数字1，但是它们越来越靠近1。我们用如下符号表示这个事情：

\[\lim_{i \rightarrow \infty }l_i=L \]

这个式子表示的意思是当\(i\)趋于无穷的时候，\(L\)为\(l_i\)的极限。

这个思想也可用于函数。我们考虑函数\(f(t)\)，我们想知道当\(t\)越来越靠近某个值（比如\(a\)）时函数值如何变化。如果当\(t\)趋近于\(a\)时，\(f(t)\)可任意接近某个值\(L\)，我们称\(t\)趋近于\(a\)时，\(f(t)\)的极限为\(L\)，记作

\[\lim_{_{t \rightarrow a} }f(t)=L \]

\(f(t)\)是变量\(t\)的函数，\(t\)变化，则\(f(t)\)也变化，微分就是讨论函数的变化率。想法是这样的，知道某瞬时的函数值为\(f(t)\)，然后让时间变化一点点，看看函数值变化多少。变化率为函数值\(f\)的变化量与自变量\(t\)变化量的比值。变化量用大写希腊字母\(\Delta\)表示，时间\(t\)的变化量即为\(\Delta t\)（注意这不是\(\Delta \times t\)）。在时间间隔\(\Delta t\)内，函数值从\(f(t)\)变化到\(f(t+\Delta t)\)，函数的变化量为

\[\Delta f=f(t+\Delta t)-f(t) \]

要精确定义时刻\(t\)时函数的变化量，必须让\(\Delta t\)趋于0，而此时，\(\Delta f\)也趋于0，但二者的比值一般不为0，有个极限值，这个极限就是\(f(t)\)对\(t\)的导数，

\begin{equation}\frac{df}{dt}=\lim_{\Delta t \rightarrow 0}\frac{\Delta f}{\Delta t} = \lim_{\Delta t \rightarrow 0}\frac{f(t+\Delta t)-f(t)}{\Delta t}\label{eq:derive}\end{equation}

现在让我们练习下求导计算。比如计算函数\(f(t)=t^2\)的导数。根据方程\ref{eq:derive}计算导数。先计算

\[f(t+\Delta t)=(t+\Delta t)^2=t^2+2t\Delta t+\Delta t^2 \]

减去\(f(t)\)，

\[f(t+\Delta t)-f(t)=(t+\Delta t)^2-t^2=2t\Delta t+\Delta t^2 \]

两边除去\(\Delta t\)，

\[\frac{f(t+\Delta t)-f(t)}{\Delta t}=\frac{2t\Delta t+\Delta t^2}{\Delta t}=2t+\Delta t \]

当\(\Delta t\)趋于0时，上式第一项不受影响，第二项将消失。记住一点：当计算导数时，\(\Delta t\)的高阶项将为0。因此，

\[\lim_{\Delta t \rightarrow 0}\frac{2t\Delta t+\Delta t^2}{\Delta t}=2t \]

即\(t^2\)的导数为

\[\frac{d(t^2)}{dt}=2t \]

下面我们考虑一般的幂函数，\(f(t)=t^n\)。先计算\(f(t+\Delta t)=(t+\Delta t)^n\)，它可由二项式定理进行计算，

\[f(t+\Delta t)=(t+\Delta t)^n=t^n+nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2 \]

\[\qquad \qquad \quad \quad \qquad \qquad \qquad \qquad +\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n \]

减去\(f(t)\)，得

\[\Delta f=f(t+\Delta t)-f(t)=t^n+nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2 \]

\[\quad \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n -t^n \]

\[\quad \quad \quad \quad \qquad \qquad \qquad =nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2 \]

\[\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n \]

除以\(\Delta t\)

\[\frac{\Delta f}{\Delta t}=nt^{n-1} + \frac{n(n-1)}{2}t^{n-2}\Delta t$$ $$\quad \quad \quad \quad \qquad \qquad \qquad +\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^2+\dots+\Delta t^{n-1} \]

令\(\Delta t \rightarrow 0\)，得导数为

\[\frac{dt^n}{dt}=nt^{n-1} \]

即便\(n\)不是整数，上式依然成立，\(n\)可为任意实数或复数。

这里说几个特例。\(n\)=0\(，此时\)f(t)=1\(，导数为0——任何常函数的导数也都为0。\)n\(=0\)，此时\(f(t)=t\)，导数为1——变量 自己对自己的导数为1。

下面列举几个常见的导数。

\[\frac{d(\sin t)}{dt}=\cos t$$ $$\frac{d(\cos t)}{dt}=-\sin t$$ \begin{equation}\frac{d(e^t)}{dt}=e^t\label{eq:et}\end{equation} $$\frac{d(\ln t)}{dt}=\frac{1}{t} \]

方程\ref{eq:et}值得说一说。如果\(t\)是整数，\(e^t\)的含义很明显，比如\(e^3=e\times e \times e\)。方程\ref{eq:et}就是\(e^t\)的定义，导数就是自身。

关于导数还有几条有用的规则。你可以作为联系证明一下。第一条规则，常数的导数为0。这容易理解，导数是变化率，而常数没有变化，因此有

\[\frac{dc}{dt}=0 \]

常数与函数\(f(t)\)乘积也是函数，它的导数等于常数乘以函数\(f(t)\)的导数，

\[\frac{d(cf)}{dt}=c\frac{df}{dt} \]

函数代数和的导数等于各个函数导数的代数和，比如两个函数\(f(t)\)和和\(g(t)\)，有如下关系：

\[\frac{d(f+g)}{dt}=\frac{d(f)}{dt}+\frac{d(g)}{dt} \]

函数的积的导数满足如下关系：

\[\frac{d(fg)}{dt}=g(t)\frac{d(f)}{dt}+f(t)\frac{d(g)}{dt} \]

\(f(g)\)是\(g\)的函数，\(g(t)\)是\(t\)的函数，那么\(f\)最终是\(t\)的函数，这种函数称为隐函数。你要是想知道某个\(t\)对应的\(f\)值，你需要先计算\(g(t)\)，然后计算\(f(g)\)。函数\(f\)对时间\(t\)的导数满足如下关系：

\[\frac{d(f)}{dt}=\frac{d(f)}{dg}\frac{d(g)}{dt} \]

这称为链式规则。链式规则可以让你想出一个中间函数，方便地计算一个复杂的函数的导数。比如计算如下函数的导数，

\[f(t)=\ln t^3 \]

设计一个中间函数\(g(t)=t^3\)，于是有\(f(g)=\ln g\)，然后应用链式规则

\[\frac{df}{dt}=\frac{df}{dg}\frac{dg}{dt} \]

应用求导公式，\(\frac{df}{dg}=\frac{1}{g}\)，\(\frac{dg}{dt}=3t^2\)，带入上式，

\[\frac{df}{dt}=\frac{3t^2}{g} \]

带入\(g(t)=t^3\)，得

\[\frac{df}{dt}=\frac{3}{t} \]

应用以上规则你可以方便地计算导数。以上基本上就是求导的所有规则。

练习1：计算以下函数的导数：$$f(t) = t^4 + 3 t^3 - 12 t^2 + t - 6$$$$g(x)=\sin x - \cos x$$$$\theta(\alpha)=e^{\alpha} + \alpha\ln \alpha$$ $$x(t)=\sin^2t-\cos t$$

（注：第4个函数原文误为\(x(t)=\sin^2x-\cos x\)）

练习2：导数的导数称为二阶导数，写为\(\frac{d^2f(t)}{dt^2}\)。计算练习1中各函数的二阶导数。

练习3：应用链式规则，计算以下函数的导数：$$g(t) = \sin(t^2) - \cos(t^2)$$ $$\theta(\alpha)=e^{3\alpha} +3\alpha\ln (3\alpha)$$ $$x(t)=\sin^2(t2)-\cos(t^2)$$

练习4：证明函数和与积的求导法则和链式规则。

练习5：证明方程\ref{eq:et}。

质点运动

质点就是把一个东西看成一个几何上的点，这显然是个理想化的概念，任何东西都不会如一个点那么小，即便是电子也不会那么小。但是，在很多情况下，我们可以忽略物体的形状，当做一个点来处理。比如地球显然不是一个点，但计算地球绕太阳公转时的轨道的时候，我们忽略地球的大小，也可以得到精度很高的结果。

质点的位置可由三个空间坐标给出，质点的运动通过每个时刻质点的位置来定义。数学上，给出三个空间坐标随时间\(t\)变化的函数:\(x(t)\)，\(y(t)\)，\(z(t)\)，即指明了一个位置。

质点在\(t\)时刻的位置还可以用矢量\(\vec{r}(t)\)表示，有三个分量\(x(t)\)，\(y(t)\)，\(z(t)\)。质点走过的路径（称为轨迹）用\(\vec{r}(t)\)表示。经典力学要干的工作就是根据初始条件和动力学定律确定出\(\vec{r}(t)\)。

除了位置，质点另外一个最重要的信息是速度。速度也是矢量。定义矢量需要一点微积分知识。

考虑一个质点在\(t\)时刻及随后晚一点点时刻\(t+\Delta t\)的位移。在这个很小的时间间隔\(\Delta t\)内，质点从\(x(t)\)，\(y(t)\)，\(z(t)\)处运动至\(x(t+\Delta t)\)，\(y(t+\Delta t)\)，\(z(t+\Delta t)\)，或者用矢量表示，从\(\vec{r}(t)\)运动至\(\vec{r}(t+\Delta t)\)处。位移可定义为：

\[\Delta x = x(t+\Delta t) - x(t)$$ $$\Delta y = y(t+\Delta t) - y(t)$$ $$\Delta z = z(t+\Delta t) - z(t) \]

或

\[\Delta \vec{r} = \vec{r}(t+\Delta t) - \vec{r}(t) \]

位移即是在质点在很短的时间\(\Delta t\)内走过的位移。速度为位移除以时间\(\Delta t\)，并取极限\(\Delta t\)趋于零。如\(x\)方向的速度为

\[v_x = \lim_{\Delta t \rightarrow 0}\frac{\Delta x}{\Delta t} \]

这实际上就是\(x\)对时间求导。

\[v_x = \frac{dx}{dt}=\dot{x}$$ $$v_y = \frac{dy}{dt}=\dot{y}$$ $$v_z = \frac{dz}{dt}=\dot{z} \]

变量上一点表示对时间求导。这可以用于任何量对时间求导。比如\(T\)表示一壶水的温度，\(\dot{T}\)表示温度的时间变化率。这种表示方法我们还会多次遇到。

一直要写\(x\)，\(y\)，\(z\)，显得很繁琐，我们可约化成一个符号。坐标的三个分量可记为\(x_i\)，速度的分量可记为\(v_i\)：

\[v_i=\frac{dx_i}{dt}=\dot{x}_i \]

其中， \(i\)取的值为\(x\)，\(y\)，\(z\)。速度也可用矢量表示：

\[\vec{v}=\frac{d\vec{r}}{dt}=\dot{\vec{r}} \]

速度的大小为\(|\vec{v}|\)，

\[|\vec{v}|^2=v_x^2+v_y^2+v_z^2 \]

速度的大小表示质点运动的快慢，也称为速率。

加速度表示速度如何变化。质点的速度如果是个常矢量，即质点的速度不发生变化，则质点没有加速度。速度是常矢量不仅仅表示速度的大小不发生变化，还表示速度的方向不发生变化。速度的大小和方向只要有其一发生变化，即速度发生变化，即有加速度。加速度是速度对时间的导数：

\[a_i=\frac{dv_i}{dt}=\dot{v_i} \]

用矢量表示：

\[\vec{a}=\frac{d\vec{v}}{dt}=\dot{\vec{v}} \]

\(v_i\)是\(x_i\)对时间的一阶导数，\(a_i\)是\(v_i\)对时间的一阶导数，因此，\(a_i\)是\(x_i\)对时间的二阶导数，

\[a_i=\frac{d^2x_i}{dt^2}=\ddot{v}_i \]

变量上面的两个点表示对时间的二阶导数。

举例

考虑一个质点，自\(t=0\)时开始运动，运动方程如下：

\[x(t)=0$$ $$y(t)=0$$ $$z(t)=z(0)+v(0)t-\frac{1}{2}gt^2 \]

很明显，质点在\(x\)和\(y\)方向上没有运动，只沿着\(z\)轴运动，常数\(z(0)\)和\(v(0)\)表示\(z\)方向上质点的初始位置和初始速度。\(g\)也是一个常数。

对时间求导，可得质点的速度，

\[v_x(t)=0$$ $$v_y(t)=0$$ $$v_z(t)=v(0)-gt \]

速度的\(x\)和\(y\)分量总是零，速度的\(z\)分量在\(t=0\)时刻的值为\(v(0)\)。

随着时间的流逝，\(-gt\)这一项就不再是零了，最终会超过\(v(0)\)，质点沿\(z\)轴负方向运动。

再对时间求一次导，可得质点加速度，

\[a_x(t)=0$$ $$a_y(t)=0$$ $$a_z(t)=-g \]

加速度沿\(z\)轴方向，是个负的常数。如果\(z\)轴竖直向上，质点向下加速，就像下落的物体那样。

下面我们考虑一个振荡的质点，质点在\(x\)方向往复运动。由于沿\(y\)和\(z\)方向没有运动，我们将其忽略。三角函数就可表示一个简单的振荡运动，

\[x(t)=\sin \omega t \]

其中，希腊字母\(\omega\)为常数，它的数值越大，表示振荡的越快，这种运动叫简谐振动，如图1所示。

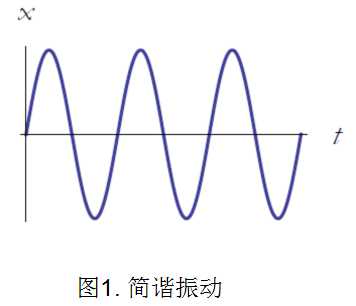
下面计算速度和加速度。\(x(t)\)对时间的一阶导数即为速度，

\[v_x=\frac{dx(t)}{dt}=\frac{d}{dt}\sin \omega t = \omega \cos \omega t \]

加速度是\(x(t)\)对时间的二阶导数，也即\(v_x(t)\)对时间的一阶导数，

\[a_x=\frac{d^2x}{dt^2}=\frac{dv_x(t)}{dt}=-\omega^2\sin \omega t \]

有一些有趣的事情值得注意。当质点处于最极大或最极小值时，质点速度为零。fangu反过来，当质点处于\(x=0\)处时，质点速度达到极大或极小。这种情况我们称质点位置与速度反相，相位差90°。见图2和图3。

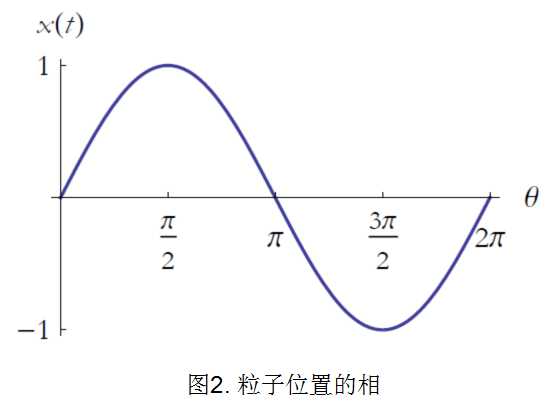
（注意：以上为原文中的两图，图中的\(\theta\)应为\(\omega t\)）

质点位置与加速度也有联系，二者都正比于\(\sin \omega t\)，但是符号相反，当质点位置是正(负)的时候，质点的加速度为负(正)。即不管质点在哪里，质点都往原点加速，位置和加速度反相，相位差为180°。

练习6：质点完成一个运动周期需要多长时间？

下一个例子，质点绕原点做匀速圆周运动，即以恒定速率沿圆周运动。我们可以不考虑\(z\)轴，只考虑\(x\), \(y\)平面上的运动。要描述这一运动，需要两个函数\(x(t)\)和\(y(t)\)。我们考虑质点沿逆时针方向运动，轨迹的半径为\(R\)。

把运动投影到\(x\)和\(y\)轴上，可以使运动更直观。质点绕着原点转圈，它的\(x\)坐标从\(-R\)到\(R\)之间来回变换，\(y\)坐标也是一样，但是\(x\)和\(y\)坐标有90°的相位差，当\(x\)坐标达到最大值，\(y\)坐标为0，反之亦然。

对于逆时针的匀速圆周运动，运动方程如下：

\[x(t)=R\cos \omega t$$ $$y(t)=R\sin \omega t \]

其中，\(\omega\)为圆频率，表示单位时间内质点转过的角的弧度。质点转一圈用的时间为运动周期：

\[T=\frac{2\pi}{\omega} \]

由运动方程就可以计算速度分量和加速度分量：

\[v_x=-R\sin \omega t$$ $$v_y=R\cos \omega t$$ $$a_x=-R^2\cos \omega t$$ $$a_y=-R^2\sin \omega t \]

可以看出圆周运动一个有趣的性质：加速度与位置矢量平行反向，即加速度的方向指向原点。牛顿曾用这个性质分析过月亮的运动。

练习7：证明位置矢量和速度矢量正交

练习8：给出以下位置矢量，计算对应的速度矢量和加速度矢量，并用画图软件作出各位置矢量及其对应的s速度矢量和加速度矢量的图。$$\vec{r}=(\cos \omega t, e^{\omega t})$$ $$\vec{r}=\left (\cos (\omega t-\phi), \sin (\omega t-\phi)\right)$$ $$\vec{r}=(c\cos^3t,c\sin3t)$$