德劳内三角化生成器Triangle研读笔记

写在前面

Jonathan Richard Shewchuk巨佬是美国伯克利大学的cs教授，他在十几年前开发出的这款Triangle程序。最近在研习3d模型布尔操作时，发现了不少开源项目都用巨佬的triangle代码来实现模型remesh(重新三角网格化)。Triangle代码注释详尽，但苦于个人是数学苦手，有些就算每个单词都认识但是组合起来就不行了；好在官网上有绘声绘色的带图片说明，我这种笨脑子也能理解个七七八八。现特地在此博文中记录我在阅读triangle文档的一些笔记，希望能对未来的自己和后来者们起到些许帮助，让巨佬的优秀成果能惠及到更多的人。

目录和文件

在triangle的官网中下载到的压缩包包含如下文件：

.
|-- A.poly      //输入样例文件
|-- makefile    //编译配置文件
|--showme.c     //图形化展示源码
|--triangle.c   //triangle头文件
|--triangle.h   //triangle源码
|--tricall.c    //调用triangle的demo

triangle就用了俩文件，加起来也就一万多行代码。(就？)支持单独编译triangle源码，用可执行文件处理数据文件；或者在别的程序里调用源码，只需要在别的程序里设置些宏定义即可(后面会讲)。
tirangle的数据文件有六种：.node，.poly, .ele, .neigh, .area, .edge，对应点集、点+线段集、三角形集、邻接集、面积集（改进细分专用）、生成边集（维诺图专用）。格式如下:

**attribute：triangle允许给每个单独的数据都设置一个属性值，这个属性值可以在后续用来制定用户的自定义规则。不需要的话attribute可以不用管。
**boundary marker:标记该数据是否是整个图形的边界(0或1)。
## 点集
First line: <# of vertices> <dimension (must be 2)> <# of attributes> <# of boundary markers (0 or 1)>
Remaining lines: <vertex #> <x> <y> [attributes] [boundary marker]

## 点+线集
First line: <# of vertices> <dimension (must be 2)> <# of attributes> <# of boundary markers (0 or 1)>
Following lines: <vertex #> <x> <y> [attributes] [boundary marker]
One line: <# of segments> <# of boundary markers (0 or 1)>
Following lines: <segment #> <endpoint> <endpoint> [boundary marker]
One line: <# of holes>
Following lines: <hole #> <x> <y>
Optional line: <# of regional attributes and/or area constraints>
Optional following lines: <region #> <x> <y> <attribute> <maximum area>

## 三角形集
First line: <# of triangles> <nodes per triangle> <# of attributes>
Remaining lines: <triangle #> <node> <node> <node> ... [attributes]

## 邻接集
First line: <# of triangles> <# of neighbors per triangle (always 3)>
Following lines: <triangle #> <neighbor> <neighbor> <neighbor>

## 面积集
First line: <# of triangles>
Following lines: <triangle #> <maximum area>

## 生成边集
First line: <# of edges> <# of boundary markers (0 or 1)>
Following lines: <edge #> <endpoint> <endpoint> [boundary marker]

功能介绍

Triangle可以完成的功能，包括在平面内的德劳内三角化、约束型三角化、规则服从三角化、维诺图等。

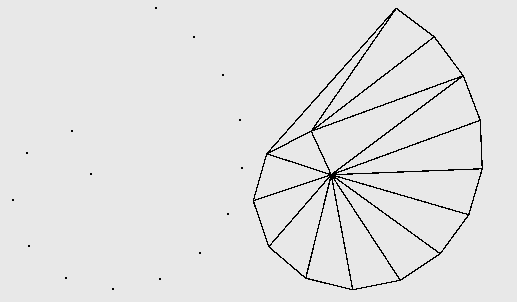
德劳内三角化(Delaunay triangulation)：输入一个点集，生成如图的三角形网格。他们满足：

• 点集里的每个点都是三角形的顶点
• 每个三角形的外接圆“内”一定没有其他点（圆上可以有）。

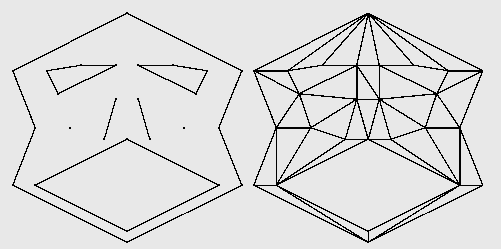
约束型三角化(Constrained Delaunay triangulation,AKA CDT):输入点的和线段的混合数据，生成如图三角型网络。他们满足：

• 输入集里的每个点都是三角形的顶点，每个线段都是三角形的边
• 每个三角形，要么外接圆里没有其他点，要么外接圆里的点和该三角形“不可见”（即圆内点和该三角形隔着至少一条贯穿圆的线）。

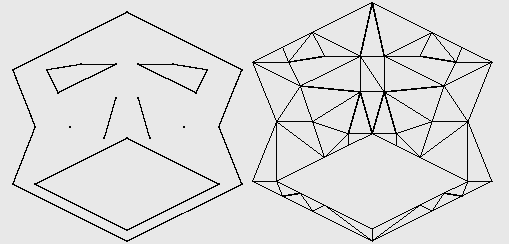
规则服从三角化（conforming constrained Delaunay triangulation，AKA CCDT）:一开始不是很懂，conform不是服从的意思嘛？服从约束三角化是什么意思？看了样例才知道，它是这个意思：

• CCDT是CDT的一个特殊情况
• CCDT服从了某些额外规则,比如三角形有最小角，比如三角形有最大面积。