C++第二次作业

C++第二次作业

---

教学目的

明白函数的用途，学会使用重载函数，分清楚值传递与地址传递，学会编写递归函数

教程

1.为什么要使用函数(函数编写好以后，可以被反复使用，使用时只关心函数的功能与使用方法，不必关心函数的具体实现，这样有利于代码重写，提高开发效率)

---

实验P66页例3-1

#include<iostream>
using namespace std;
double power(double x,int n){
    double val=1.0;
    while(n--)
    val*=x;
    return val;
}
int main()
{
    cout<<"5 to power 2 is"<<power(5,2)<<endl;
}

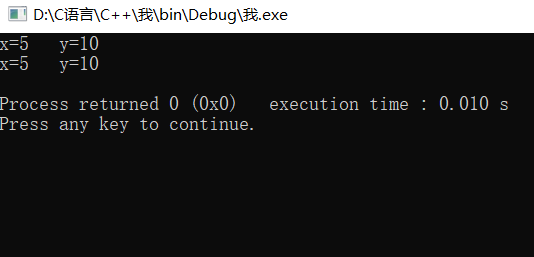
之后若在需要计算m的n次方时只需要改函数中的参数值即可

---

2.为什么要用函数重载（方便使用，便于记忆，因为C++允许功能相近的函数在相同的作用域内相同的函数名定义）

---

注意：重载函数的形参必须不同：个数不同或者类型不同
例题P85页例3-16

---

3.值传递与地址传递（函数的参数传递就是形参与实参相结合的过程，形式结合的方式有值传递与地址传递）实验P78页例3-11

#include<iostream>
using namespace std;
void swap(int a,int b){
    int t=a;
    a=b;
    b=t;
}
int main()
{
    int x=5,y=10;
    cout<<"x="<<x<<"   y="<<y<<endl;
    swap(x,y);
    cout<<"x="<<x<<"   y="<<y<<endl;
    return 0;
}

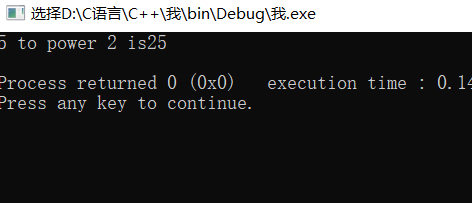
无法进行交换便是因为采用的是值传递，传递时是实参的值，是单向传递过程，形参值改变对实参不起作用

而采用地址传递则可以解决此问题代码就应改为

#include<iostream>
using namespace std;
void swap(int &a,int &b){
    int t=a;
    a=b;
    b=t;
}

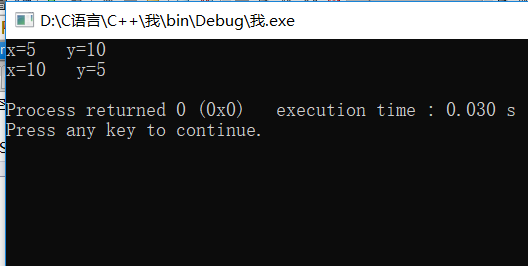
4.使用递归函数
实验汉诺塔问题
递归函数的思想在于如何实现问题与具体每一步如何实现无关，以汉诺塔为例，思想就在于：第一步以C盘为媒介将A盘上n-1个盘子移到B盘，具体如何移无所谓，第二步将A盘是上最后一个盘子放到C。第三步将B盘上n-1个盘子以A盘为媒介放到C盘

#include<iostream>
using namespace std;
void move(char src,char dest){
    cout<<src<<"-->"<<dest<<endl;
}
void hanoi(int n,char src,char medium,char dest){
    if(n==1)
        move(src,dest);
    else{
        hanoi(n-1,src,dest,medium);//以C为媒介A->B(n-1)
        move(src,dest);//移最后一个盘子
        hanoi(n-1,medium,src,dest);//以A为媒介B->C(n-1)
    }
}
int main()
{
    int m;
    cout<<"Enter the number of diskes:";
    cin>>m;
    cout<<"the step to moving"<<m<<"diskes:"<<endl;
    hanoi(m,'A','B','C');
    return 0;
}

---

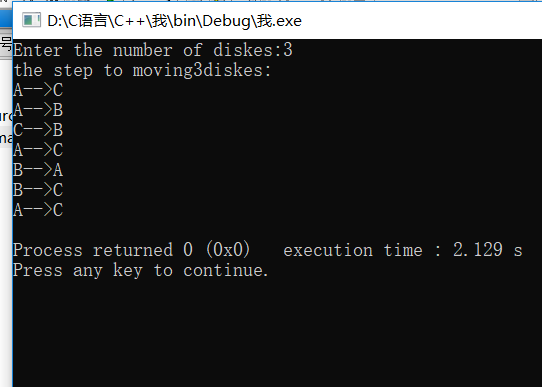
课后应加强练习，多思考