亚特兰蒂斯

题目描述

有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。
其中一些甚至包括岛屿部分地图。
但不幸的是，这些地图描述了亚特兰蒂斯的不同区域。
您的朋友 Bill 必须知道地图的总面积。
你自告奋勇写了一个计算这个总面积的程序。

输入格式

输入包含多组测试用例。
对于每组测试用例，第一行包含整数 n，表示总的地图数量。
接下来 n 行，描绘了每张地图，每行包含四个数字 x1,y1,x2,y2（不一定是整数），(x1,y1) 和 (x2,y2) 分别是地图的左上角位置和右下角位置。
注意，坐标轴 x 轴从上向下延伸，y 轴从左向右延伸。
当输入用例 n=0 时，表示输入终止，该用例无需处理。

输出格式

每组测试用例输出两行。
第一行输出 Test case #k，其中 k 是测试用例的编号，从 1 开始。
第二行输出 Total explored area: a，其中 a 是总地图面积（即此测试用例中所有矩形的面积并，注意如果一片区域被多个地图包含，则在计算总面积时只计算一次），精确到小数点后两位数。
在每个测试用例后输出一个空行。

数据范围

\(1≤n≤10000,0≤x1<x2≤100000,0≤y1<y2≤100000\)
注意，本题 n 的范围上限加强至 10000。

输入样例：

2
10 10 20 20
15 15 25 25.5
0

输出样例：

Test case #1
Total explored area: 180.00 

思路

假设给的图像是这样。

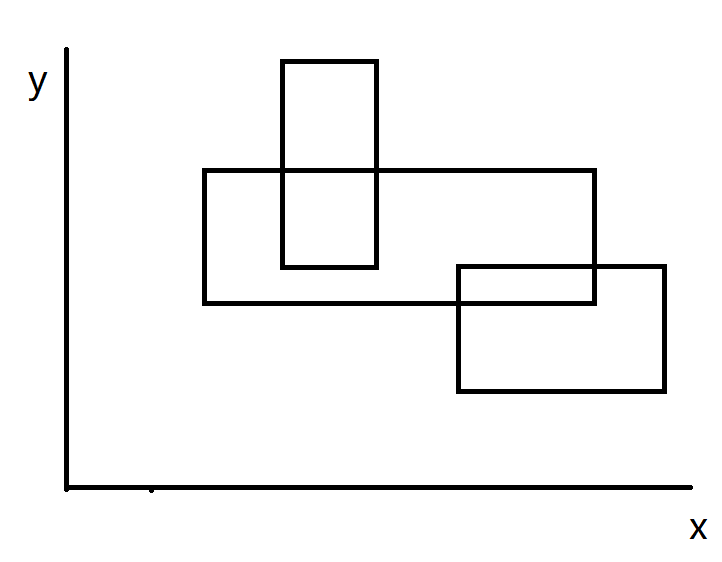
实际要求的面积是这样

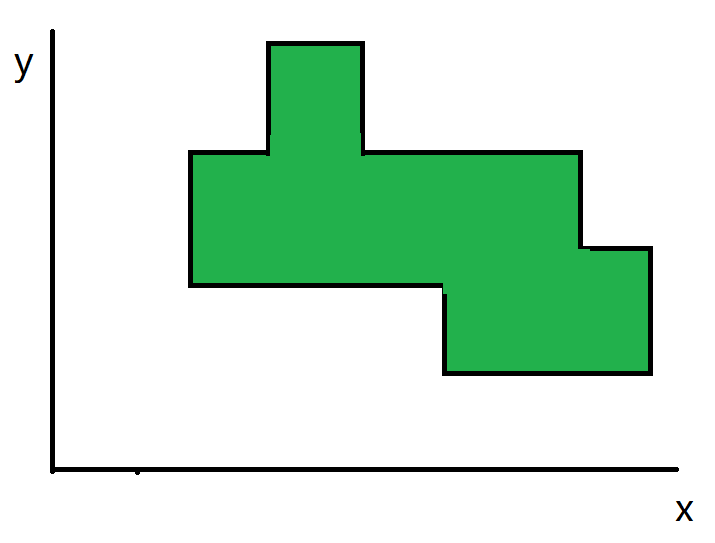
我们先来想暴力的思路。假设每个坐标都是整数，那就是一行一行的数有多少个格子被涂上了颜色。
这样显然会TLE，但是我们的思路不变，想想怎么才能优化这个数格子的步骤。
首先我们想到每个竖线到下一个竖线前它的len值肯定是不变的，那么我们就不需要一行一行的数了，只需要在对于每一道竖线那数一下，然后乘上竖线之间的差。
那么接下来的问题是怎么能快速算出每一个竖线所对应的长度。由于在每个x那都可能修改还有查询，这样大量的区间查询与修改操作，我们难免会想到线段树。
那么我们就把初始每个矩形的左边标记为+1表示矩形开始，右边标记为-1表示这个矩形结束。被标记为正数的区域即线段长度。
这题所采用的x，y都是double类型的需要我们进行离散化。
接下来面临的问题是怎么去维护这个线段树。
我们不需要查询函数，因为每次的查询都是对于整个区间查询长度，即\(tr[1].len\)，由此我们也省略了\(pushdown()\)函数。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = 1e6 + 10;

struct Seg{
	double x, y1, y2;
	int k;
	bool operator < (const Seg& t) const {
		return x < t.x;
	}
}s[N];
struct Node{
	int l, r;
	int cnt;
	double len;
}tr[N];

vector<double> all;

inline int find(double y){
	return lower_bound(all.begin(), all.end(), y) - all.begin();
}
void pushup(int u){
	if(tr[u].cnt)
		tr[u].len = all[tr[u].r + 1] - all[tr[u].l];
	else if(tr[u].l != tr[u].r)
		tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
	else tr[u].len = 0;
}
void build(int u, int l, int r){
	tr[u] = { l, r, 0, 0 };
	if(l != r){
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
	}
}
void modify(int u, int l, int r, int d){
	if(tr[u].l >= l && tr[u].r <= r)tr[u].cnt += d;
	else {
		int mid = tr[u].l + tr[u].r >> 1;
		if(l <= mid)modify(u << 1, l, r, d);
		if(r > mid)modify(u << 1 | 1, l, r, d);
	}
	pushup(u);
}
int main(){
	int n, t = 1;
	while(scanf("%d", &n), n){
		all.clear();
		for(int i = 0, j = 0; i < n; i++){
			double x1, x2, y1, y2;
			scanf("%lf %lf %lf %lf", &x1, &y1, &x2, &y2);
			s[j++] = { x1, y1, y2, 1 };
			s[j++] = { x2, y1, y2, -1 };
			all.push_back(y1), all.push_back(y2);
		}
		sort(all.begin(), all.end());
		all.erase(unique(all.begin(), all.end()), all.end());
		build(1, 0, all.size() - 2);
		sort(s, s + n * 2);
		double res = 0;
		for(int i = 0; i < n * 2; i++){
			if(i)res += tr[1].len * (s[i].x - s[i - 1].x);
			modify(1, find(s[i].y1), find(s[i].y2) - 1, s[i].k);
		}
		printf("Test case #%d\nTotal explored area: %.2lf\n\n", t++, res);
	}
	return 0;
}