树状数组笔记

引言

当我们只需要在一段数据中进行修改，那么最快的显然只需要一个数组就能进行\(O(1)\)的修改操作。
而当我们需要查询一段数据的前缀和，那么我们只需要\(sum[i] = sum[i - 1] + a[i]\)的去维护一个前缀和数组就可以处理在\(O(1)\)的复杂度内这个问题。
那么当我们既需要进行对一段数据进行修改，又需要查询前缀和的时候，上述的两种方法显然都不太合适，对数组计算前缀和和对前缀和数组进行修改操作都是需要\(O(n)\)的复杂度的。
那么我们就需要考虑怎么才能得到一个均衡的方法同时能够处理这两个问题。

树状数组

对于每次查询前缀和都去现算显然是不合适的，我们需要采取一个方式去记录前缀和的数据，但是传统的前缀和数组在修改时要面临后面的所有的数据都要去修改也是不合适的，所以我们可以考虑用一个数组，它的每个元素只表示一段数据的和，这样就能同时兼顾两者的优点，在修改的时候仅需要修改一部分的值，求和的时候也只需要将每一段加起来，这样两种计算的时间复杂度都降到了\(O(log ~ n)\)。
那么我们需要考虑的就是怎样去取每一段的长度才能做到最优化的效果。假设\(n = 2^{k_1} + 2^{k_2} + ...+2^{k_i}\)，这里我们采用\(C(n)\)表示\([x - 2^{k_i} + 1, x]\)，\(k_i\)表示\(x\)最低的一位1所在的位，采取\(lowbit(x)\)即\(x & -x\)我们可以很容易的得到\(2^k\)。而求前缀和就是将\([x - 2^{k_i} + 1, x]\)，\([x - 2^{k_i} - 2^{k_{i-1}} + 1, x - 2^{k_i}]\)，等这些长度为\(O(log~n)\)的区间加起来就行。

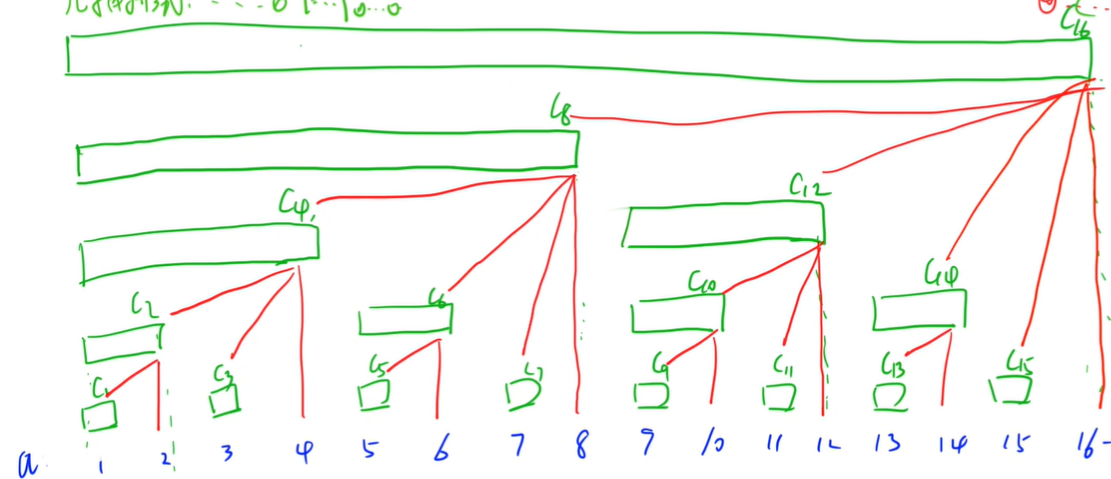
上图是树状数组的经典示例图，假设我们要求\(sum(7)\)，因为7的二进制表示是111，即\(7 = 2^2 + 2^1 + 2^0\)。那么\(sum(7) = C(7) + C(6) + C(4)\)。
所以\(sum\)函数如下

int sum(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(i))res += tri[i];
	return res;
}

由\(sum\)函数我们也可以发现其实\(C(x)\)的修改只会影响唯一一个父节点，所以修改函数如下

void add(int x, int v) {
	for (int i = x; i <= n; i += lowbit(i))tri[i] += v;
}