Raney 引理

设整数序列 \(\{ A_n \}\)，前缀和 \(S_i = A_1 + A_2 + \ldots + A_i\).
若 \(S_n = 1\)，则在 \(\{ A_n \}\) 的 \(n\) 个循环表示中，有且仅有一个序列 \(\{ B_n \}\)，满足 \(\{ B_n \}\) 的任意前缀和均大于 \(0\).

证

考虑几何证明，在笛卡尔系中绘制 \((i, S_i)\) 的折线图，作一条斜率为 \(\frac 1 n\) 的直线，将其平移至与折线下端相切，以切点为循环序列的终点，构造出的序列即为 \(\{ B_n \}\).

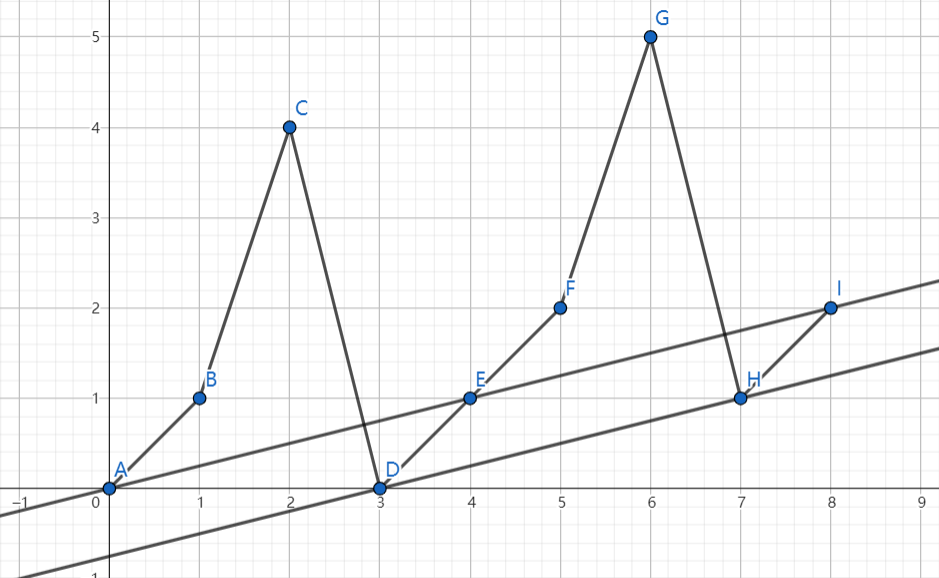
充分性：不难发现，在构造出来的序列中满足 \(S_i \ge \frac i n > 0\).

必要性：若直线与折线不相切，则必有交点，且交点前后至少存在一个点 \((i, S_i)\) 使得 \(S_i < \frac i n\)，即 \(S_i \le 0\)，矛盾.

\(\mathrm{Q.E.D.}\)