On Adjusting the Learning Rate in Frequency Domain Echo Cancellation With Double-Talk

摘要

  回声消除的主要困难之一是学习率需要根据双方通话和回声路径变化等条件而变化。在本文中，我们提出了一种改变频域回声消除器学习率的新方法。该方法基于推导 NLMS 算法在存在噪声的情况下的最优学习率。该方法与多延迟块频域 (MDF) 自适应滤波器一起评估。我们证明它比当前的双方对话检测技术表现更好，并且易于实现。

  在回声消除中需要一种方法来调整学习率，以解决信号中存在的噪声和/或干扰问题。大多数回声消除算法试图检测双方通话情况，然后通过冻结自适应滤波器的适应来做出反应。 Gänsler提出的最常用的双方通话检测算法是基于远端和近端信号之间的相干性。该算法有两个主要缺点。首先，检测阈值取决于回波路径损耗、说话者与噪声之间的能量比。其次，相干性的估计需要关于回声延迟的良好知识（或估计）。 Benesty提出的双方通话检测器消除了对显式延迟估计的需要，并且通常降低了所需的复杂度。然而，用于计算决策变量ξ的简化是基于滤波器已经收敛的假设。当回波路径改变时，这个假设不成立。

  在本文中，我们提出了一种新方法来使自适应回声消除对双方通话具有鲁棒性。我们没有尝试显式检测双方通话条件，而是使用连续学习率变量。学习率根据干扰（噪声和双向通话）以及滤波器的失调进行调整。这是通过在存在噪声的情况下推导归一化最小均方 (NLMS) 滤波器的最佳学习率并将结果应用于多延迟块频域 (MDF) 自适应滤波器来完成的。在本文中，我们专注于设计学习率以在双方通话条件下快速做出反应。

  在第二节中，我们推导了 NLMS 算法在存在噪声的情况下的最佳学习率。在第三节中，我们提出了一种基于对 NLMS 滤波器获得的推导来调整 MDF 算法的学习率的技术。第四节介绍了实验结果和讨论，第五节总结了本文。

存在噪声时的最佳 NLMS 学习率

  从信息论的角度来看，我们知道只要自适应滤波器没有完美调整，误差信号总是包含一些关于精确（时变）滤波器权重$w_{k}(n)$的信息。然而，关于$w_{k}(n)$的新信息量随着麦克风信号$d(n)$中的噪声量而减少。在 NLMS 滤波器的情况下，这意味着当噪声增加或滤波器失调减少时（随着滤波器收敛），随机梯度变得不太可靠。在本节中，我们推导出复数NLMS算法的一般情况下的最佳学习率。

  长度为 N 的复数 NLMS 滤波器定义为：

$$e(n)=d(n)-\hat{y}(n)=d(n)-\sum_{k=0}^{N-1} \hat{w}_{k}(n) x(n-k)$$

  滤波器更新步骤：

$$\begin{aligned}
\hat{w}_{k}(n+1) &=\hat{w}_{k}(n)+\mu \frac{e(n) x^{*}(n-k)}{\sum_{i=0}^{N-1}|x(n-i)|^{2}} \\
&=\hat{w}_{k}(n)+\mu \frac{\left(d(n)-\sum_{i} \hat{w}_{i}(n) x(n-i)\right) x^{*}(n-k)}{\sum_{i=0}^{N-1}|x(n-i)|^{2}}
\end{aligned}$$

其中$x(n)$是远端信号，$w_{k}(n)$是时间$n$的估计滤波器权重， $\mu$是学习率。

  考虑滤波器权重的误差$\delta_{k}(n)=\hat{w}_{k}(n)-w_{k}(n)$，并且已知$d(n)=v(n)+\sum_{k} w_{k}(n) x(n-k)$，则上式可改写为：

$$\delta_{k}(n+1)=\delta_{k}(n)+\mu \frac{\left(v(n)-\sum_{i} \delta_{i}(n) x(n-i)\right) x^{*}(n-k)}{\sum_{i=0}^{N-1}|x(n-i)|^{2}}$$

  在每个时间步，滤波器失调函数$\Lambda(n)=\sum_{k} \delta_{k}^{*}(n) \delta_{k}(n)$可写做：

$$\Lambda(n+1)=\sum_{k=0}^{N-1}\left||\delta_{k}(n)+\mu \frac{\left(v(n)-\sum_{i} \delta_{i}(n) x(n-i)\right) x^{*}(n-k)}{\sum_{i=0}^{N-1}|x(n-i)|^{2}}\right||^{2}$$

  假设$x(n)$和$v(n)$是彼此不相关的白噪声信号，我们发现：

$$E\{\Lambda(n+1) \mid \Lambda(n), x(n)\}=\Lambda(n)\left[1-\frac{2 \mu}{N}+\frac{\mu^{2}}{N}+\frac{\mu^{2} \sigma_{v}^{2}}{\Lambda(n) \sum_{i=0}^{N-1}|x(n-i)|^{2}}\right]$$

其中期望算子$E\{\cdot\}$仅在此时接管$v(n)$并且$\sigma_{v}^{2}=E\left\{|v(n)|^{2}\right\}$。因为上式是一个凸函数，所以可以通过求解当$\Lambda(n) \neq0$时，$\partial E\{\Lambda(n+1)\} / \partial \mu=0$ 来最小化相对于$\mu$的预期失调：

$$\frac{-2}{N}+\frac{2 \mu}{N}+\frac{2 \mu \sigma_{v}^{2}}{\Lambda(n) \sum_{i=0}^{N-1}|x(n-i)|^{2}}=0$$

  这导致了条件最优学习率（以当前的失调和远端信号为条件）：

$$\mu_{o p t}(n)=\frac{1}{1+\frac{\sigma_{v}^{2}}{\Lambda(n)(1 / N) \sum_{i=0}^{N-1}|x(n-i)|^{2}}}$$

  当没有近端噪声$\left(\sigma_{v}^{2}\right)$时，我们可以看到上式简化为$\mu_{o p t}(n)=1$。现在，考虑到$\Lambda(n) \sum_{i=0}^{N-1}|x(n-i)|^{2} / N$在$x(n)$上的期望等于残余回波$r(n)=y(n)-\hat{y}(n)$的方差$\sigma_{r}^{2}(n)$，并且知道输出信号方差为$\sigma_{e}^{2}(n)=\sigma_{v}^{2}(n)+\sigma_{r}^{2}(n)$，我们近似（随着$N$趋近于无穷大，近似变得精确) 最优学习率为：

  $$\hat{\mu}_{o p t}(n)\approx \frac{\sigma_{r}^{2}(n)}{\sigma_{e}^{2}(n)}$$

  这意味着最佳学习率与残差与错误率大致成正比。请注意，$\sigma_{e}^{2}(n)$可以很容易地估计，但是残余回波$\sigma_{r}^{2}(n)$的估计是困难的，将在下一节中讨论。现在，如果我们假设我们有估计$\hat{\sigma}_{r}^{2}(n)$和$\hat{\sigma}_{e}^{2}(n)$，我们可以选择学习率：

$$\hat{\mu}_{o p t}(n)=\min \left(\frac{\hat{\sigma}_{r}^{2}(n)}{\hat{\sigma}_{e}^{2}(n)}, 1\right)$$

其上限是无噪声情况下的最佳速率，反映了$\sigma_{e}^{2}(n)$始终大于$\sigma_{r}^{2}(n)$的事实。

  滤波器的自适应会在以下情况下停止($E\{\Lambda(n+1)\}=\Lambda(n)$)：

$$\Lambda(n) \approx \frac{\sigma_{v}^{2}}{\sigma_{x}^{2}\left(\frac{2}{\mu}-1\right)}$$

其中$\sigma_{x}^{2}(n)$ 是滤波器输入（远端）信号的方差。将$\hat{\mu}_{o p t}(n)$值代入式中，我们得到在滤波器自适应停止时，残余回波为：

$$\sigma_{r}^{2}(n) \approx \min \left(\frac{1}{2} \hat{\sigma}_{r}^{2}(n), \sigma_{v}^{2}(n)\right)$$

其中$\min (\cdot)$的第一个参数通过求解下式获得：

$$\sigma_{r}^{2}(n)=\frac{\sigma_{v}^{2}(n)}{\frac{2\left(\sigma_{r}^{2}(n)+\sigma_{v}^{2}(n)\right)}{\hat{\sigma}_{r}^{2}(n)}-1}$$

上式结果意味着残余回波以背景噪声和估计残余回波的一半为界，以较低者为准。出于这个原因，重要的是不要将残余回声高估超过 3 dB，至少在双方通话期间是这样。

应用背景噪声和双向对话的 MDF 算法

  第2节的推导假设$x(n)$和$v(n)$是白噪声信号。显然该假设不适用于使用NLMS算法对语音信号进行回声消除的情况，但我们建议将其应用于在频域中运行的自适应滤波器算法。在本节中，我们专注于多延迟块频域 (MDF) 自适应滤波器。用于 MDF 算法（和其他块频率算法）的适配类似于为每个频率独立应用NLMS算法。已经观察到，与原始时域信号相比，输入信号在时间上（跨连续 FFT 帧）的相关性较低。此外，学习率$\mu(k, \ell)$可以与频率相关。在本节中，变量$\hat{Y}(k, \ell)$和$E(k, \ell)$是$\hat{y}(n)$和$e(n)$的频域对应项，其中$k$是频率索引，$\ell$是帧索引。

  假设 MDF 算法的每个频率的信号在时间上不相关，我们通过以下方式近似最优的频率相关学习率：

$$\mu_{o p t}(k, \ell) \approx \frac{\sigma_{r}^{2}(k, \ell)}{\sigma_{e}^{2}(k, \ell)}$$

其中$k$是离散频率，$\ell$是帧索引。为了估计残余回波$\sigma_{r}^{2}(k, \ell)$，我们假设自适应滤波器具有与频率无关的泄漏系数$\eta(\ell)$表示滤波器的失调。这导致估计：

$$\hat{\sigma}_{r}^{2}(k, \ell) = \hat{\eta}(\ell) \hat{\sigma}_{\hat{Y}}^{2}(k, \ell)$$

其中$\hat{\eta}(\ell) $是估计的泄漏系数。该公式的优点在于它将残差估计$\sigma_{r}^{2}(k, \ell)$ 分解为一个缓慢演化但难以估计的项 ($\hat{\eta}(\ell)$) 和一个快速演化但易于估计的项 ($ \hat{\sigma}_{\hat{Y}}^{2}(k, \ell)$)。泄漏系数$\eta(\ell)$实际上是滤波器的回波抑制比 (ERLE) 的倒数。

  我们希望学习率在双方对话的情况下具有快速响应，以防止在双方对话开始时滤波器发散。出于这个原因，我们使用瞬时估计$\hat{\sigma}_{y}(k, \ell)=|Y(k, \ell)|^{2}$和$\hat{\sigma}_{e}(k, \ell)=|E(k, \ell)|^{2}$。这导致学习率：

$$\hat{\mu}_{o p t}(k, \ell)=\min \left(\hat{\eta}(\ell) \frac{|\hat{Y}(k, \ell)|^{2}}{|E(k, \ell)|^{2}}, \mu_{\max }\right)$$

其中$\mu_{\max }$是一个设计参数（总是小于或等于1），它为实际目的设置了学习率的上限，并确保学习率不会导致自适应滤波器变得不稳定。

  我们从中看到，滤波器失调和双方通话的影响是分离的。因此，即使残余回声（泄漏系数）的估计需要更长的时间段，学习率也可以对双方通话做出快速反应。需要解决的一个重要方面是初始条件。初始化滤波器时，所有权重都设置为零，因此$Y(k, \ell)$信号也为零。这导致使用上式计算的学习率为零。为了开始适应过程，学习率$\mu(k, \ell)$设置为一个固定常数（我们使用 $\mu(k, \ell)= 0.25$），持续时间等于滤波器长度的两倍（仅非零部分信号的$x(n)$被考虑在内）。此过程仅在滤波器初始化时是必需的，在回波路径改变的情况下不需要。

A. 泄漏估计

  最优学习率很大程度上取决于估计的泄漏系数$\hat{\eta}(\ell)$。我们建议通过利用信号的非平稳性并使用估计回波的功率谱与输出信号之间的线性回归来估计泄漏系数${\eta}(\ell)$。这种选择是基于这样一个事实，即残余回波的频谱与估计的回波频谱高度相关，而回波频谱与噪声频谱(近场语音频谱？)之间没有相关性。首先，使用一阶直流抑制滤波器获得功率谱的零均值版本：

 $$\begin{aligned}
P_{Y}(k, \ell)=&(1-\gamma) P_{Y}(k, \ell-1) \\
&+\gamma\left(|\hat{Y}(k, \ell)|^{2}-|\hat{Y}(k, \ell-1)|^{2}\right)
\end{aligned}$$

 $$\begin{aligned}
P_{E}(k, \ell)=&(1-\gamma) P_{E}(k, \ell-1) \\
&+\gamma\left(|E(k, \ell)|^{2}-|E(k, \ell-1)|^{2}\right)
\end{aligned}$$

其中，$\hat{\eta}(\ell) $等于估计的回波功率$P_{Y}(k, \ell)$和输出功率$P_{E}(k, \ell)$之间的线性回归系数：

$$\hat{\eta}(\ell)=\frac{\sum_{k} R_{E Y}(k, \ell)}{\sum_{k} R_{Y Y}(k, \ell)}$$

其中相关系数$R_{E Y}(k, \ell)$和$R_{Y Y}(k, \ell)$递归平均为：

$$\begin{aligned}
R_{E Y}(k, \ell) &=(1-\beta(\ell)) R_{E Y}(k, \ell)+\beta(\ell) P_{Y}(k) P_{E}(k) \\
R_{Y Y}(k, \ell) &=(1-\beta(\ell)) R_{Y Y}(k, \ell)+\beta(\ell)\left(P_{Y}(k)\right)^{2} \\
\beta(\ell) &=\beta_{0} \min \left(\frac{\hat{\sigma}_{\hat{Y}}^{2}(\ell)}{\hat{\sigma}_{e}^{2}(\ell)}, 1\right)
\end{aligned}$$

$\beta_{0}$是泄漏估计的基础学习率，并且$\hat{\sigma}_{\hat{Y}}^{2}(\ell)$和$\hat{\sigma}_{\hat{e}}^{2}(\ell)$分别是估计回波和输出信号的总功率。可变平均参数$\beta(\ell)$可防止在不存在回波时调整估计值。

B. 双方通话、背景噪声和回声路径变化

  可以看出，上面描述的自适应学习率能够在没有显式建模的情况下处理双方对话和回声路径变化。当双方发生对话时，分母$|E(k, \ell)|^{2}$迅速增加，导致学习率瞬时下降，只持续到双方对话的时间。在背景噪声的情况下，学习率取决于回波信号的存在以及泄漏估计。随着滤波器失调变小，学习率也会变小。双方对话检测中涉及的一个主要困难是需要区分双方对话和回声路径变化，这两者都会导致滤波器误差信号的突然增加。这种区别是通过泄漏估计来完成的。在双方对话的情况下，误差的功率谱与估计回波的功率谱之间几乎没有相关性，因此$\hat{\eta}(\ell)$保持很小，学习率也很小。另一方面，当回波路径发生变化时，功率谱之间存在很大的相关性，这会导致$\hat{\eta}(\ell)$ 的快速增加。

结果与讨论

  所提出的系统在具有背景噪声、双方对话和回声路径变化的声学回声消除环境中进行评估。使用的两种不同的脉冲响应长度为 1024 个样本，并且是从一个小办公室的真实录音中测量的，麦克风和扬声器都放在桌子上。

  将所提出的算法与 Gänsler 双重通话检测器、归一化互相关方法以及没有双重通话检测（无 DTD）的基线进行比较。对于典型的 32 秒场景，近端和远端的信号如图 2a) 所示，回波路径在 16 秒后发生变化。对于所有算法，测量的回波损耗增强 (ERLE) 如图 2b)所示。由于算法行为的自然变化，因此无法立即从该图中确定最准确的算法。但是，我们在这里展示它是为了展示我们算法的行为。例如，可以观察到，当回声路径在 16 秒后发生变化时，所提出的算法重新适应的速度快于其他具有双方通话检测的算法，并且几乎与没有双方通话检测的回声消除器一样快

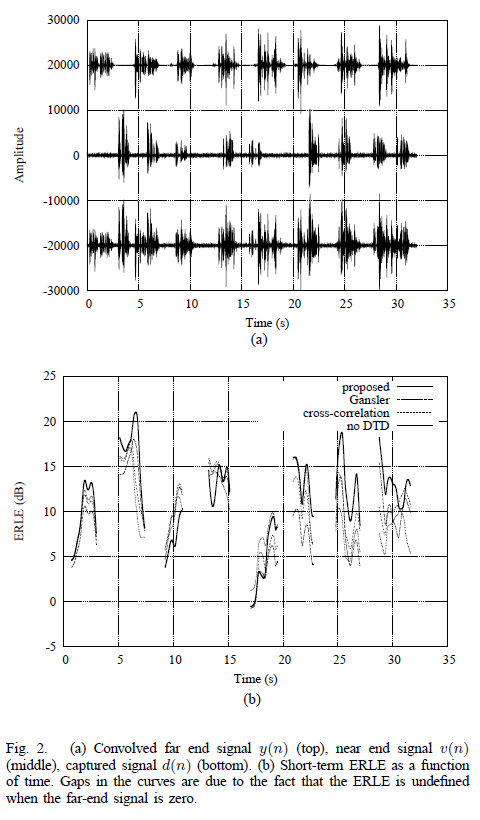
  图 3 提供了 ERLE 的估计值（计算为$1/\hat{\eta}(\ell)$）。可以观察到，估计值大致遵循测量的 ERLE，尽管估计值明显有噪声。最重要的是，它几乎从不高估残余回声（低估 ERLE）超过 3 dB。此外，当回波路径发生变化时，估计值迅速下降到 0 dB，这是所需的行为。

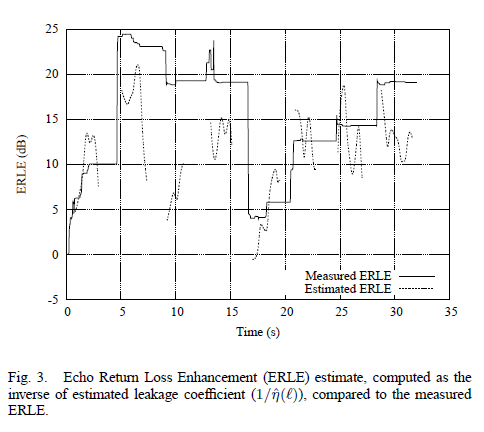
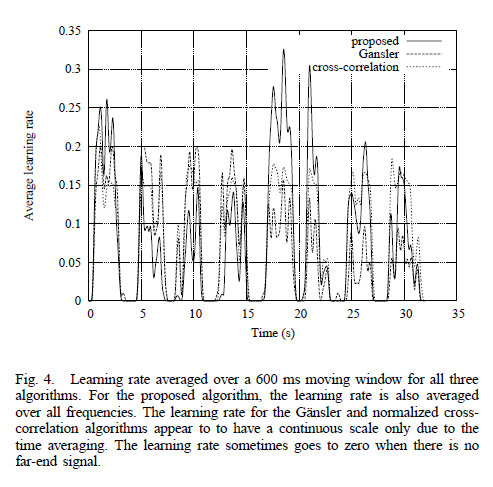
  图 4 显示了所有三种算法的学习率如何随时间变化。当在 t = 16 s 处回波路径变化后学习率迅速上升时，可以清楚地观察到泄漏估计的效果，保持远高于其他算法的学习率约 5 秒。还观察到，随着过滤器变得更好地适应，学习率下降。与 Gänsler 和不考虑滤波器失调的归一化互相关算法相比，这是一个优势。