自适应步长算法

Variable Step-Size NLMS Algorithm for Under-Modeling Acoustic Echo Cancellation

介绍

声学回声消除（AEC）是自适应滤波最流行的应用之一。自适应滤波器的作用是识别终端扬声器和麦克风之间的声学​​回声路径，即房间声学脉冲响应。尽管许多自适应算法在理论上适用于 AEC，但在精度和处理能力有限的应用中，归一化最小均方 (NLMS) 算法及其某些版本（例如，频域或子带版本）最常用。该算法的性能，在收敛速度、失调和稳定性方面，由步长参数控制。在稳定条件下，该参数的选择一方面反映了快速收敛速度和良好的跟踪能力与另一方面低失调之间的权衡。为了满足这些相互冲突的要求，需要控制步长。因此，已经提出了许多可变步长 NLMS (VSS-NLMS) 算法。本文提出了一种非参数 VSS-NLMS (NPVSS-NLMS) 算法，该算法在 AEC中具有良好的性能。

一般来说，这些算法是在假设精确建模情况下开发的，即自适应滤波器的长度等于必须建模的系统的长度。由于声学回波路径非常长，欠建模情况（即自适应滤波器的长度小于回波路径的长度）经常发生。系统无法建模的部分引起的残余回波可以解释为附加噪声，它会影响算法的性能。我们提出了一种在欠建模情况下派生的 VSS-NLMS 算法。该算法不需要任何有关声学环境的额外信息，因此在实际 AEC 应用中高效且易于控制。

适用于欠建模场景的 VSS-NLMS 算法

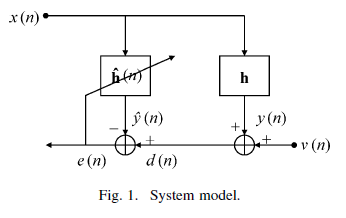
系统模型配置如图 1 所示，其中目标是使用长度为L的自适应滤波器对长度未知的系统进行建模。假设两个系统都是有限脉冲响应滤波器，由实值向量定义

$$\begin{aligned}
\mathbf{h} &=\left[\begin{array}{llll}
h_{0} & h_{1} & \ldots & h_{N-1}
\end{array}\right]^{T} \\
\hat{\mathbf{h}}(n) &=\left[\begin{array}{llll}
\hat{h}_{0}(n) & \hat{h}_{1}(n) & \cdots & \hat{h}_{L-1}(n)
\end{array}\right]^{T}
\end{aligned}$$

n为时间索引。

考虑建模不足的情况，当$L<N$的情况下，我们可以写作$y(n)=y_{L}(n)+y_{N-L}(n)$，$x(n)=\left[\mathbf{x}_{L}^{T}(n)\mathbf\quad{x}_{N-L}^{T}(n)\right]^{T}$，$h=\left[\mathbf{h}_{L}^{T}(n)\mathbf\quad{h}_{N-L}^{T}(n)\right]^{T}$。则

$$\mathbf{h}_{L}=\left[\begin{array}{llll}
h_{0} & h_{1} & \ldots & h_{L-1}
\end{array}\right]^{T}$$

$$\mathbf{h}_{N-L}=\left[\begin{array}{llll}
h_{L} & h_{L+1} & \ldots & h_{n-L+1}
\end{array}\right]^{T}$$

$$\mathbf{x}_{L}(n)=\left[\begin{array}{llll}
x(n) & x(n-1) & \ldots & x(n-L+1)
\end{array}\right]^{T}$$

$$\mathbf{x}_{N-L}(n)=\left[\begin{array}{llll}
x(n-L) & x(n-L-1) & \ldots & x(n-N+1)
\end{array}\right]^{T}$$

$$y_{L}(n)=\mathbf{x}_{L}^{T}(n) \mathbf{h}_{L}$$

$$y_{N-L}(n)=\mathbf{x}_{N-L}^{T}(n) \mathbf{h}_{N-L}$$

因此，先验误差信号可表示为：

$$\begin{aligned}
e(n) &=d(n)-\hat{y}(n)=d(n)-\mathbf{x}_{L}^{T}(n) \hat{\mathbf{h}}(n-1) \\
&=\mathbf{x}_{L}^{T}(n)\left[\mathbf{h}_{L}-\hat{\mathbf{h}}(n-1)\right]+y_{N-L}(n)+v(n)
\end{aligned}$$

后验误差信号可表示为：

$$\varepsilon(n)=\mathbf{x}_{L}^{T}(n)\left[\mathbf{h}_{L}-\hat{\mathbf{h}}(n)\right]+y_{N-L}(n)+v(n)$$

基于梯度的自适应算法的更新方程是：

$$\hat{\mathbf{h}}(n)=\hat{\mathbf{h}}(n-1)+\mu(n) \mathbf{x}_{L}(n) e(n)$$

后验和先验误差信号之间的关系为

$$\varepsilon(n)=e(n)\left[1-\mu(n) \mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)\right]$$

为了在稳定性条件下导出步长参数，可以选择几种方法。一个可能的解决方案是假设$\varepsilon(n)=0$，$e(n) \neq 0$。因此， 经典 NLMS 算法的步长即为$\mu_{N L M S}(n)=\left[\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)\right]^{-1}$。应该注意的是，这种方法适用于无噪声情况（即$v(n)=0$）和精确建模情况（即$N=L$）。在实践中，一个正适应常数（通常小于 1）乘以这个步长，以在收敛速度和失调之间实现适当的折衷。在存在噪声和建模不足的情况下若让后验误差强制为0，则：

$$\mathbf{x}_{L}^{T}(n)\left[\mathbf{h}_{L}-\hat{\mathbf{h}}(n)\right]=-y_{N-L}(n)-v(n) \neq 0$$

这将使得自适应滤波器估计产生偏差。在这种情况下，$\mathbf{x}_{L}^{T}(n)\left[\mathbf{h}_{L}-\hat{\mathbf{h}}(n)\right]=0$意味着
$$\varepsilon(n)=e(n)\left[1-\mu(n) \mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)\right]=y_{N-L}(n)+v(n)$$

因此，在这种情况下推导的更合理的方法选择$\mu(n)$ ，使得$E\left\{\varepsilon^{2}(n)\right\}=E\left\{y_{N-L}^{2}(n)\right\}+E\left\{v^{2}(n)\right\}$，其中$E\{{\bullet}\}$表示数学期望。并且$y_{N-L}(n)$与$v(n)$是不相关的。并假设$\mathbf{x}^{T}(n) \mathbf{x}(n)=LE\left\{x^{2}(n)\right\} \text { for } L \gg 1$（这在自适应滤波器长度约为数百的 AEC 中有效），我们发现

$$\begin{aligned}
E\left\{e^{2}(n)\right\}[1-L \mu(n) E&\left.\left\{x^{2}(n)\right\}\right]^{2} =E\left\{y_{N-L}^{2}(n)\right\}+E\left\{v^{2}(n)\right\} .
\end{aligned}$$

步长参数的解是

$$\mu(n)=\frac{1}{\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)}\left[1-\sqrt{\frac{E\left\{y_{N-L}^{2}(n)\right\}+E\left\{v^{2}(n)\right\}}{E\left\{e^{2}(n)\right\}}}\right]$$

假设$y_{L}(n)$与$y_{N-L}(n)$是不相关的，我们得到

$$E\left\{y_{N-L}^{2}(n)\right\}=E\left\{d^{2}(n)\right\}-E\left\{y_{L}^{2}(n)\right\}-E\left\{v^{2}(n)\right\}$$

考虑到自适应滤波器系数已经收敛到一定程度，可以假设

$$E\left\{y_{L}^{2}(n)\right\}=E\left\{\hat{y}^{2}(n)\right\}$$

因此步长参数可表示为：

$$\mu(n)=\frac{1}{\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)}\left[1-\sqrt{\frac{E\left\{d^{2}(n)\right\}-E\left\{\hat{y}^{2}(n)\right\}}{E\left\{e^{2}(n)\right\}}}\right]$$

在实际中，上式写为：

$$\mu(n)=\frac{1}{\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)}\left[1-\frac{\sqrt{\hat{\sigma}_{d}^{2}(n)-\hat{\sigma}_{\hat{y}}^{2}(n)}}{\hat{\sigma}_{e}(n)}\right]$$

一般来说，参数$\hat{\sigma}_{\alpha}^{2}(n)$表示序列$\alpha(n)$的功率估计，并且可以计算为

$$\hat{\sigma}_{\alpha}^{2}(n)=\lambda \hat{\sigma}_{\alpha}^{2}(n-1)+(1-\lambda) \alpha^{2}(n)$$

其中$\lambda$是加权因子，值为$\lambda=1-1/(KL)$，其中$K>1$。$\hat{\sigma}_{\alpha}^{2}(0)$初始值为0。

在步长参数计算中，为了避免被小数除法，需要在第一个分母上添加一个正常数$\delta$，称为正则化因子。该参数的值随着噪声水平的增加而增加，同时考虑到环境噪声和建模不足的噪声，可进一步优化。此外，在式中添加一个较小的正值$\xi$，以避免被零除。其次，我们将开始迭代时使用 NLMS 步长（带正则化）启动算法，直到$y(n)=y_{L}(n)$并且系数估计仅受系统噪声$v(n)$影响。

综上所述，所提出的用于欠建模的VSS-NLMS（VSS-NLMS-UM）算法的步长参数为

$$\mu(n)=\left\{\begin{array}{ll}
\mu_{N L M S}(n), & \text { for } n \leq L \\
\frac{1}{\delta+\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)} \mid 1-\frac{\sqrt{\hat{\sigma}_{d}^{2}(n)-\hat{\sigma}_{\hat{y}}^{2}(n)}}{\xi+\hat{\sigma}_{e}(n)}, & \text { for } n>L
\end{array}\right.$$

所有关于声学环境变化的信息（例如，回声路径变化，环境噪声变化）都包含在第二个比率中。因此，所提出的算法在实际环境中更加稳健且更易于控制。

仿真结果

当输入信号$x(n)$为白色高斯输入信号时，加权因子$\lambda$采用$K=2$，为语音信号时，$K=6$。在算法的步长内，我们固定$\xi=0.0001$，算法的正则化因子为$\delta=30 \sigma_{x}^{2}$，其中$\sigma_{x}^{2}$是输入信号的功率。

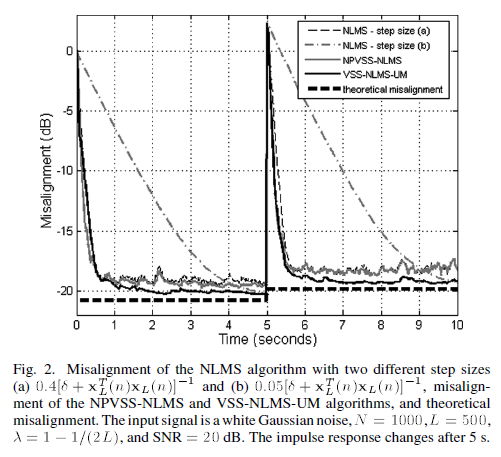
图比较了 NLMS 算法在两种不同步长下的性能，(a)$0.4\left[\delta+\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)\right]^{-1}$ (B)$0.05\left[\delta+\mathbf{x}_{L}^{T}(n) \mathbf{x}_{L}(n)\right]^{-1}$，为探究NPVSS-NLMS 和 VSS-NLMS-UM 算法在初始收敛速度和跟踪能力方面的性能。通过将声学脉冲响应向右移动 12 个样本，引入了声学环境的突然变化，除了步长较小的 NLMS 算法收敛慢，所有算法的初始收敛速度几乎相同。与 NPVSS-NLMS 算法相比，VSS-NLMS-UM 算法的最终偏差略低。其值与理论值非常接近，也与NLMS算法以较小步长实现的值非常接近。如果我们使用 NLMS算法，在第一次迭代中使用较大的步长，然后再使用较小的步长，将实现初始快速收敛速度和较低的错位。然而，由于步长较小，该算法在回波路径发生变化时反应较慢。

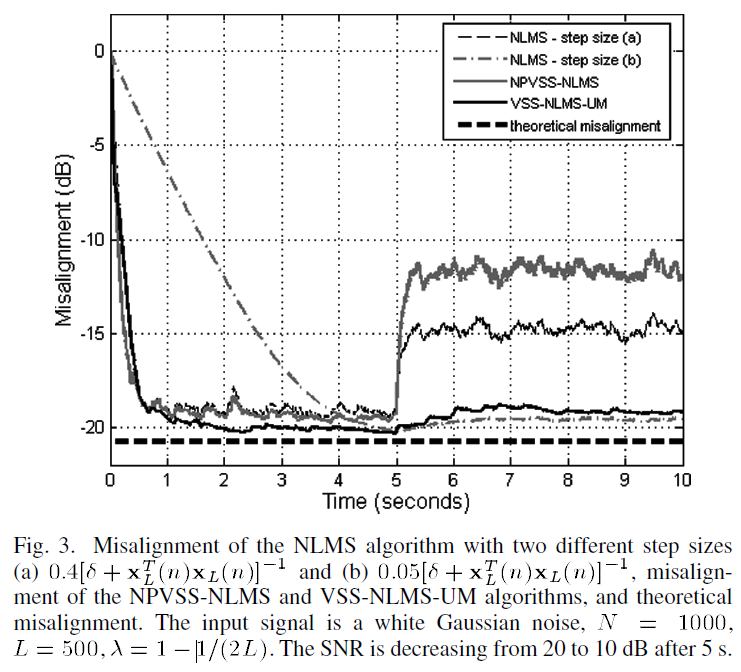
AEC 中的另一种可能情况是环境噪声的增加。如果这在静默期间没有发生，则新的噪声功率估计将不适用于NPVSS-NLMS算法。在图中，我们比较了这种情况下算法的行为，当5秒后，SNR从20变为10dB。虽然步长较大的NLMS算法和NPVSS-NLMS算法会受到这种变化的影响，但所提出的 VSS-NLMS-UM 算法几乎不受这种修改的影响。在未对齐方面，它的执行类似于具有较小步长的NLMS算法。VSS-NLMS-UM算法不需要估计噪声功率。有关系统噪声的信息包含在参数中。

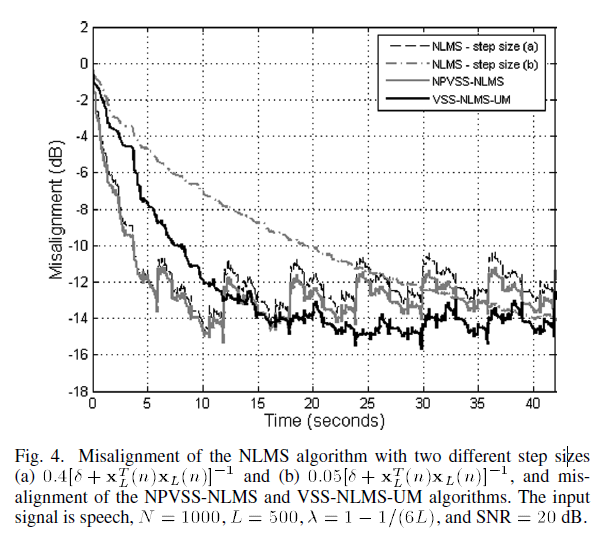
在图中，我们比较了使用语音作为输入时算法的性能。在这种情况下，可变步长 NLMS 算法优于 NLMS 算法。

结论

在 AEC 应用中，由于声学回声路径过长，自适应滤波器最有可能在建模不足的情况下工作。由系统部分无法建模引起的残余回波类似于附加噪声，它会干扰算法的性能。大多数自适应算法都没有考虑到这一方面。在本文中，我们推导出了一种适用于欠建模上下文的 VSS-NLMS 算法。最重要的是，该算法不需要任何有关声学环境的额外信息，因此非常适合实际环境的 AEC 应用。在欠建模 AEC 场景中执行的仿真结果表明 VSS-NLMS-UM 算法具有良好的性能。最后，应该注意的是，所提出算法的思想可以与其他基于 NLMS 的算法结合使用，例如频域或子带版本，这些算法在 AEC 上下文中经常使用。

 

A Nonparametric VSS NLMS Algorithm

介绍

本文提出一个新的非参数VSS-NLMS算法，在实际应用中非常容易控制。在声学回声消除背景下的仿真表明，所提出的算法比NLMS性能好得多，具有快速收敛、良好的跟踪和低的失调。

非参数 VSS-NLMS 算法

在本节中，我们描述了模型，推导了所提出的算法，并展示了与最优变量正则化 NLMS 算法的重要联系。

A. Model

以下系统输出信号：

$$y(n)=\mathbf{h}^{T} \mathbf{x}(n)+v(n)$$

其中$n$是时间索引，上标$T$表示转置

$$\mathbf{h}=\left[\begin{array}{llll}
h_{0} & h_{1} & \cdots & h_{L-1}
\end{array}\right]^{T}$$

是用自适应滤波器仿真的的未知长度系统

$$\mathbf{x}(n)=\left[\begin{array}{llll}
x(n) & x(n-1) & \cdots & x(n-L+1)
\end{array}\right]^{T}$$

是最近的$L$个输入向量，包含系统输入信号的最新样本$x(n)$，$v(n)$是独立于输入信号$x(n)$的系统噪声。我们假设$v(n)$是平稳的，并且所有信号都是实值和零均值。

B. Derivation of the Algorithm

我们将先验和后验误差信号分别定义为：

$$\begin{aligned}
e(n) &=y(n)-\hat{\mathbf{h}}^{T}(n-1) \mathbf{x}(n) \\
&=\mathbf{x}^{T}(n)[\mathbf{h}-\hat{\mathbf{h}}(n-1)]+v(n)
\end{aligned}$$

$$\begin{aligned}
\varepsilon(n) &=y(n)-\hat{\mathbf{h}}^{T}(n) \mathbf{x}(n) \\
&=\mathbf{x}^{T}(n)[\mathbf{h}-\hat{\mathbf{h}}(n)]+v(n)
\end{aligned}$$

其中滤波器长度为$L$，$\hat{\mathbf{h}}(n-1)$和$\hat{\mathbf{h}}(n)$是系统$h$在时间$n-1$和$n$的估计值。考虑线性更新方程

$$\hat{\mathbf{h}}(n)=\hat{\mathbf{h}}(n-1)+\mu(n) \mathbf{x}(n) e(n)$$

其中$\mu(n)$是一个称为步长的正标量，用于控制沿选定方向的变化。经典的NLMS步长更新为

$$\hat{\mathbf{h}}(n)=\hat{\mathbf{h}}(n-1)+\frac{\mathbf{x}(n)}{\mathbf{x}^{T}(n) \mathbf{x}(n)} e(n)$$

虽然上述过程在没有噪声的情况下是有意义的，但在存在噪声时，$\mathbf{x}^{T}(n)[\mathbf{h}-\hat{\mathbf{h}}(n)]=-v(n) \neq=0$，事实上，我们想让$\mathbf{x}^{T}(n)[\mathbf{h}-\hat{\mathbf{h}}(n)]=0$ , 这意味着$\varepsilon(n)=v(n)$。因此，我们希望以这样的方式找到步长参数$\mu(n)$：

$$E\left\{\varepsilon^{2}(n)\right\}=\sigma_{v}^{2}, \forall n$$

其中$E\{\cdot\}$表示数学期望， $\sigma_{v}^{2}=E\left\{v^{2}(n)\right\}^{2}$是系统噪声的功率。使用近似值$\mathbf{x}^{T}(n) \mathbf{x}(n)=L \sigma_{x}^{2}=L E\left\{x^{2}(n)\right\} \text { for } L \gg 1$，其中$\sigma_{x}^{2}$是输入信号的功率，得到：

$$\begin{aligned}
E\left\{\varepsilon^{2}(n)\right\} &=\left[1-\mu(n) L \sigma_{x}^{2}\right]^{2} \sigma_{e}^{2}(n) \\
&=\sigma_{v}^{2}
\end{aligned}$$

其中$\sigma_{e}^{2}(n)=E\left\{e^{2}(n)\right\}$是误差信号的功率。我们可以得到一个二次方程：

$$\mu^{2}(n)-\frac{2}{L \sigma_{x}^{2}} \mu(n)+\frac{1}{\left(L \sigma_{x}^{2}\right)^{2}}\left[1-\frac{\sigma_{v}^{2}}{\sigma_{e}^{2}(n)}\right]=0$$

因此

$$\begin{aligned}
\mu_{\operatorname{NPVSS}}(n) &=\frac{1}{\mathbf{x}^{T}(n) \mathbf{x}(n)}\left[1-\frac{\sigma_{v}}{\sigma_{e}(n)}\right] \\
&=\mu_{\mathrm{NLMS}}(n) \alpha(n)
\end{aligned}$$

其中$\alpha(n)[0 \leq \alpha(n) \leq 1]$是标准化的步长。因此，非参数 VSS-NLMS (NPVSS-NLMS) 算法为：

$$\hat{\mathbf{h}}(n)=\hat{\mathbf{h}}(n-1)+\mu_{\operatorname{NPVSS}}(n) \mathbf{x}(n) e(n)$$

在算法收敛之前，$\sigma_{e}(n)$与$\sigma_{v}$相比较大；因此$\mu_{\mathrm{NPVSS}}(n) \approx \mu_{\mathrm{NLMS}}(n)$。另一方面，当算法开始收敛到真实的解时，$\sigma_{e}(n) \approx \sigma_{v}$且$\mu_{\mathrm{NPVSS}}(n) \approx 0$ 。因此算法具有良好的收敛性和低失调。

算法步骤如下

需要提前知道$\sigma_{v}^{2}$，其可以在没有回声信号期间估计，即假设近端信号为高斯白噪声信号，$\sigma_{v}^{2}$值不变，因此可通过仅有近端信号时估计得到。

 

A VARIABLE STEP-SIZE PROPORTIONATE NLMS
ALGORITHM FOR ECHO CANCELLATION

介绍

在本文中，我们提出了 IPNLMS 算法和可变步长 NLMS (VSS-NLMS) 算法之间的组合。 VSS 方法为任何自适应系统所需的快速收敛和低失调的冲突要求提供了一种简单而有效的解决方案。此外，由于IPNLMS的特点，该算法对回声路径的特性不太敏感，适用于网络和声学回声消除应用。

PNLMS 算法背景

PNLMS 算法为每个滤波器系数分配一个单独的步长，这样一个较大的系数接收一个较大的增量，从而提高该系数的收敛速度。因此，主动系数比非主动系数（即小系数或零系数）调整得更快，因此当只有一小部分系数显著时，PNLMS算法比 NLMS收敛得更快，用于稀疏脉冲响应。更新方程如下：

$$\hat{h}(n)=\hat{h}(n-1)+\frac{\mu G(n-1) x(n) e(n)}{x^{T}(n) G(n-1) x(n)+\delta_{P N L M S}}$$

其中$ G(n – 1)$ 为对角矩阵，用于调整滤波器各个抽头的步长，$\delta_{P N L M S}=\delta_{N L M S} / L$是PNLMS算法的正则化因子。$G(n)$的对角元素，用$g_{l}(n)$表示，$0≤l≤L– 1$，计算方式如下：

$$\begin{array}{c}
\gamma_{l}(n)=\max \left\{\rho \max \left\{\delta_{p},\left|\hat{h}_{0}(n)\right|,\left|\hat{h}_{1}(n)\right|, \ldots,\left|\hat{h}_{L-1}(n)\right|\right\}\left|\hat{h}_{l}(n)\right|\right\}, \\
g_{l}(n)=\frac{\gamma_{l}(n)}{\sum_{i=0}^{L-1} \gamma_{i}(n)} .
\end{array}$$

参数$\rho$和$\delta_{p}$是正数，典型值$\rho=5/L$和$\delta_{p}=0.01$。常数$\rho$防止非常小的系数停止，当所有系数在初始化时为零时，参数$\rho$规范更新。

PNLMS 算法的主要限制是它为大系数分配了过多的自适应增益以加速它们的收敛，代价是在初始快速收敛阶段之后，该算法会变慢，甚至比 NLMS 还要慢。 IPNLMS 算法使用了一个更简单的选择。在这种情况下，G(n) 的元素计算为：

$$g_{l}(n)=\frac{1-\alpha}{2 L}+(1+\alpha) \frac{\left|\hat{h}_{l}(n)\right|}{2 \sum_{i=0}^{L-1} \hat{h}_{i}(n)+\xi} \text {, for } 0 \leq l \leq L-1$$

其中 –1 ≤ α ≤ 1，而 ξ 是一个非常小的正数，以避免被零除，尤其是在滤波器的所有抽头都初始化为零的自适应开始时。对于 α = –1，IPNLMS 和 NLMS 算法是等价的，而对于接近 1 的 α，IPNLMS 算法的行为类似于 PNLMS 算法。在实践中，参数 α 的最佳选择是 0 或 –0.5。 IPNLMS 算法的正则化参数应取为$\delta_{\text {IPNLMS }}==\delta_{\mathrm{NLMS}}(1-\alpha) / 2L$。 IPNLMS 算法在稀疏和非稀疏脉冲响应方面都优于 PNLMS。

可变步长 PNLMS 算法

将NPVSS-NLMS算法（第二篇）的思想应用于IPNLMS算法，IPNLMS算法的更新关系写成如下：

$$\hat{h}(n)=\hat{h}(n-1)+\mu(n) G(n-1) x(n) e(n)$$

其中 G(n) 是由 IPNLMS 算法中G(n) 给出的元素的对角矩阵构成。同时，后验误差与先验误差的关系为：

$$\varepsilon(n)=e(n)\left[1-\mu(n) {x}^{\mathrm{T}}(n) {G}(n-1) {x}(n)\right]$$

对前面的方程求平方，然后取两边的期望值，最后得到步长更新公式为：

$$\mu_{\mathrm{NPVSS}-\operatorname{PNLMS}}(n)=\frac{1}{{x}^{\mathrm{T}}(n){G}(n-1){x}(n)+\delta_{\mathrm{NPVSS}-I P N L M S}}\left[1-\frac{\sigma_{v}}{\xi+\sigma_{e}(n)}\right]$$

其中$\delta_{\text {NPVSS-IPNLMS }}=\delta_{\text {IPNLMS }}$是正则化因子，而ξ（小正常数）用于避免被零除。误差信号的功率估计为

$$\sigma_{e}^{2}(n)=\lambda \sigma_{e}^{2}(n-1)+(1-\lambda) e^{2}(n)$$

当 σe(n) < σv 时，$\mu_{\mathrm{NPVSS}-\operatorname{PNLMS}}(n)$ 设置为 0。我们将此算法称为非参数 VSS 改进 PNLMS (NPVSS-IPNLMS) 算法。在算法收敛之前，σe(n) 比 σv 大，因此自适应步长接近 1，这提供了最快的收敛。当算法开始收敛到真解时，σe≈σv 和$\mu_{\text {NPVSS-IPNLMS }}(n) \approx 0$。事实上，这是自适应算法所期望的行为，导致良好的收敛性和低失调。

与NPVSS-NLMS算法（第二篇）一致，仿真中需已知σv的值