Penchick Online Mathematical Olympiad, Qualifying Test 1, III.4
原题链接:https://artofproblemsolving.com/community/c4h3687790_1st_penchick_online_mathematical_olympiad_qualifying_test_1_iii4
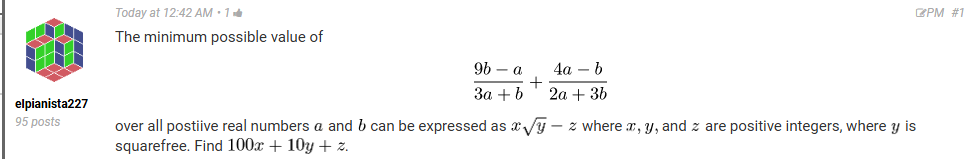
解答:
令![]() ,
, ![]() . (统一分母)
. (统一分母)
整理得:![]() 代入原式
代入原式
![]()
![]()
均值不等式(AM-GM)得到最小 ![]() , 答案为
, 答案为![]() .
.
原题链接:https://artofproblemsolving.com/community/c4h3687790_1st_penchick_online_mathematical_olympiad_qualifying_test_1_iii4
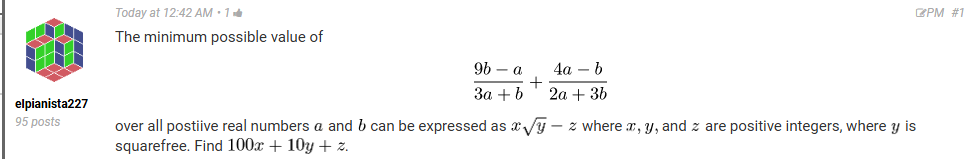
解答:
令![]() ,
, ![]() . (统一分母)
. (统一分母)
整理得:![]() 代入原式
代入原式
![]()
![]()
均值不等式(AM-GM)得到最小 ![]() , 答案为
, 答案为![]() .
.
