pytorch深度学习04

反向传播back propagation

引入：由上节课简单的linear（只有一层简单的网络），通过计算随机梯度下降训练模型（即计算loss对w的偏导来更新），从而引申到复杂网络（多个w）中。

 

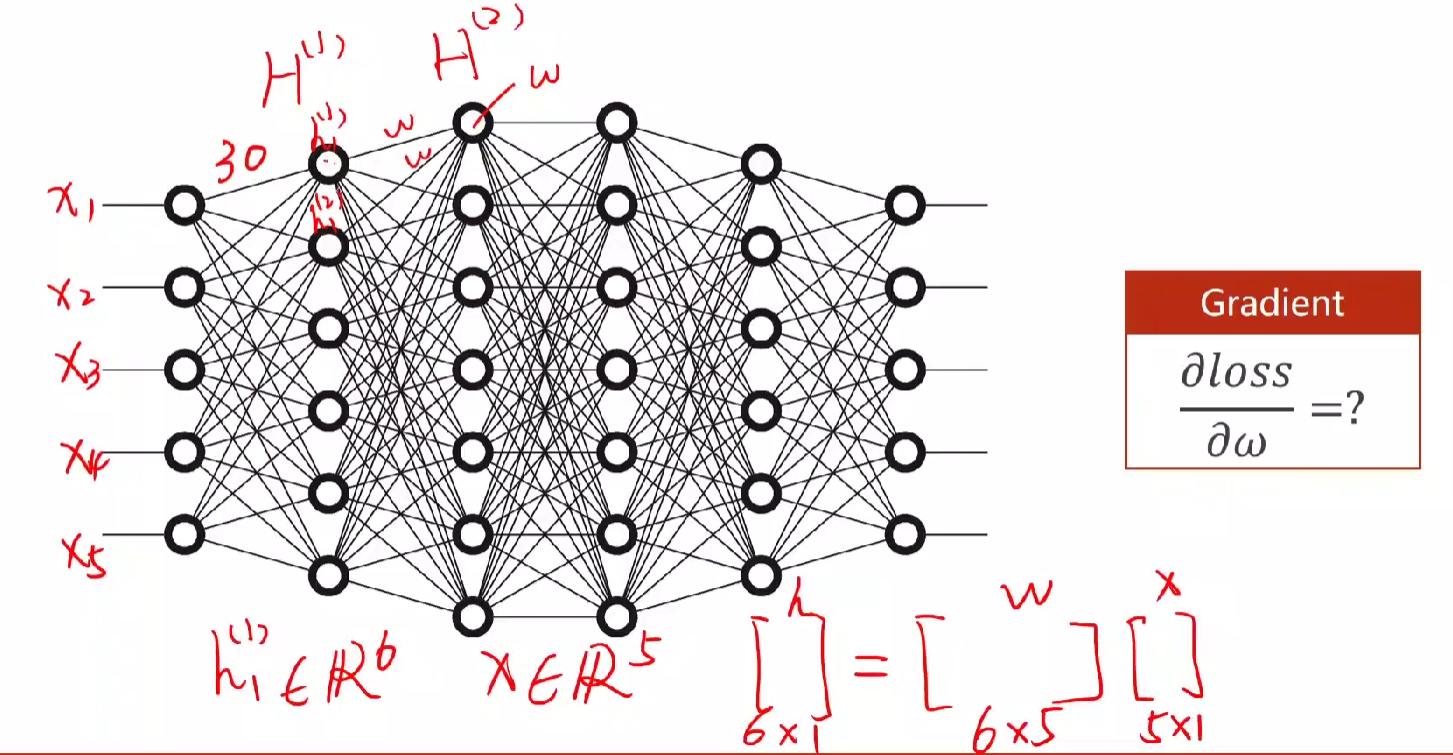
第一列为输入层，中间部分为隐藏层，最后一列为输出层。通过隐藏层，从输入的五维变成六维，即乘w的矩阵，如上图30，42，49，····

 

 计算图Computational Graph

下面例举一个两层的神经网络（ps，计算神经网络层数就是看它有几层具有计算能力的层数，而输入部分不算，因此层数为隐藏层+输出层

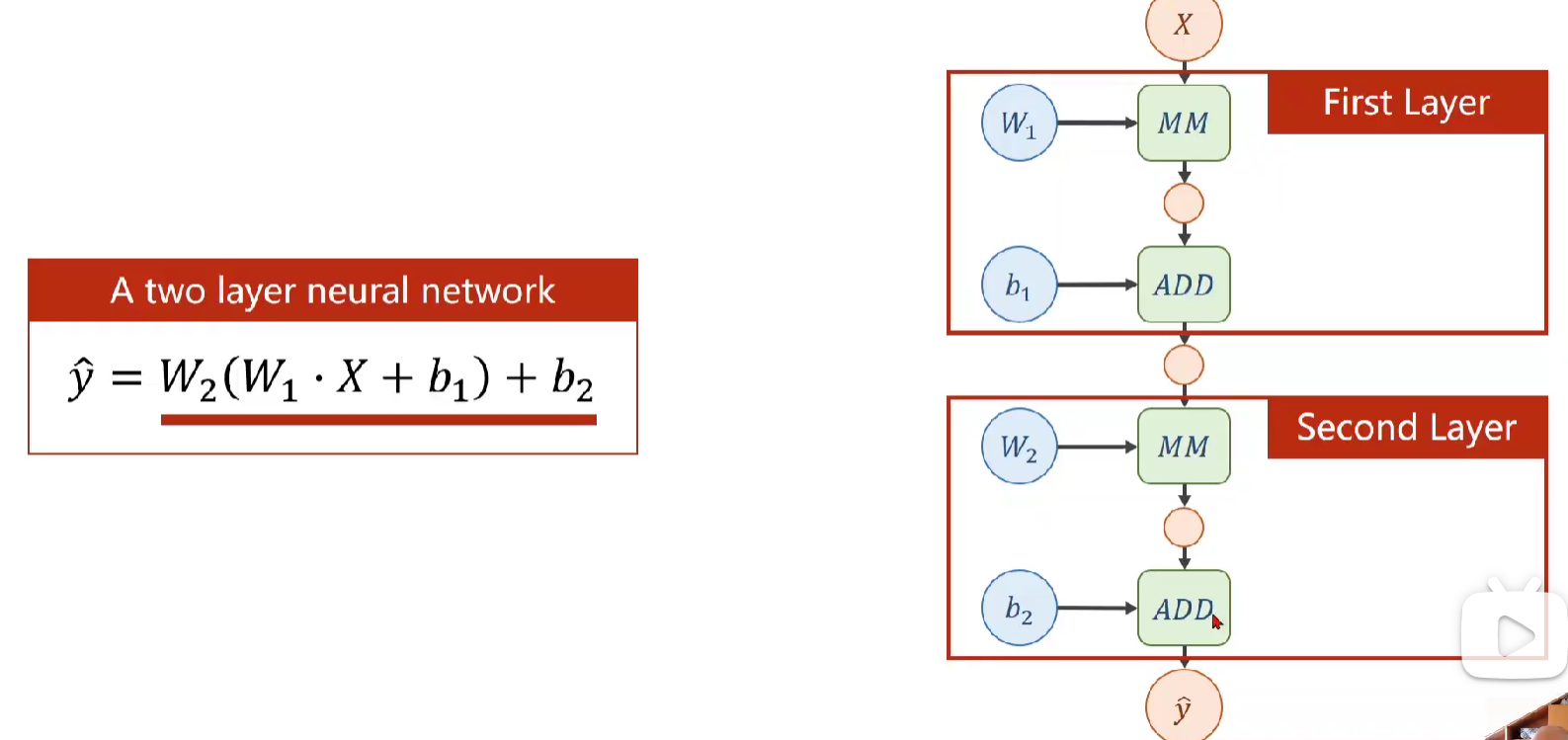MM、ADD为矩阵乘法、加法

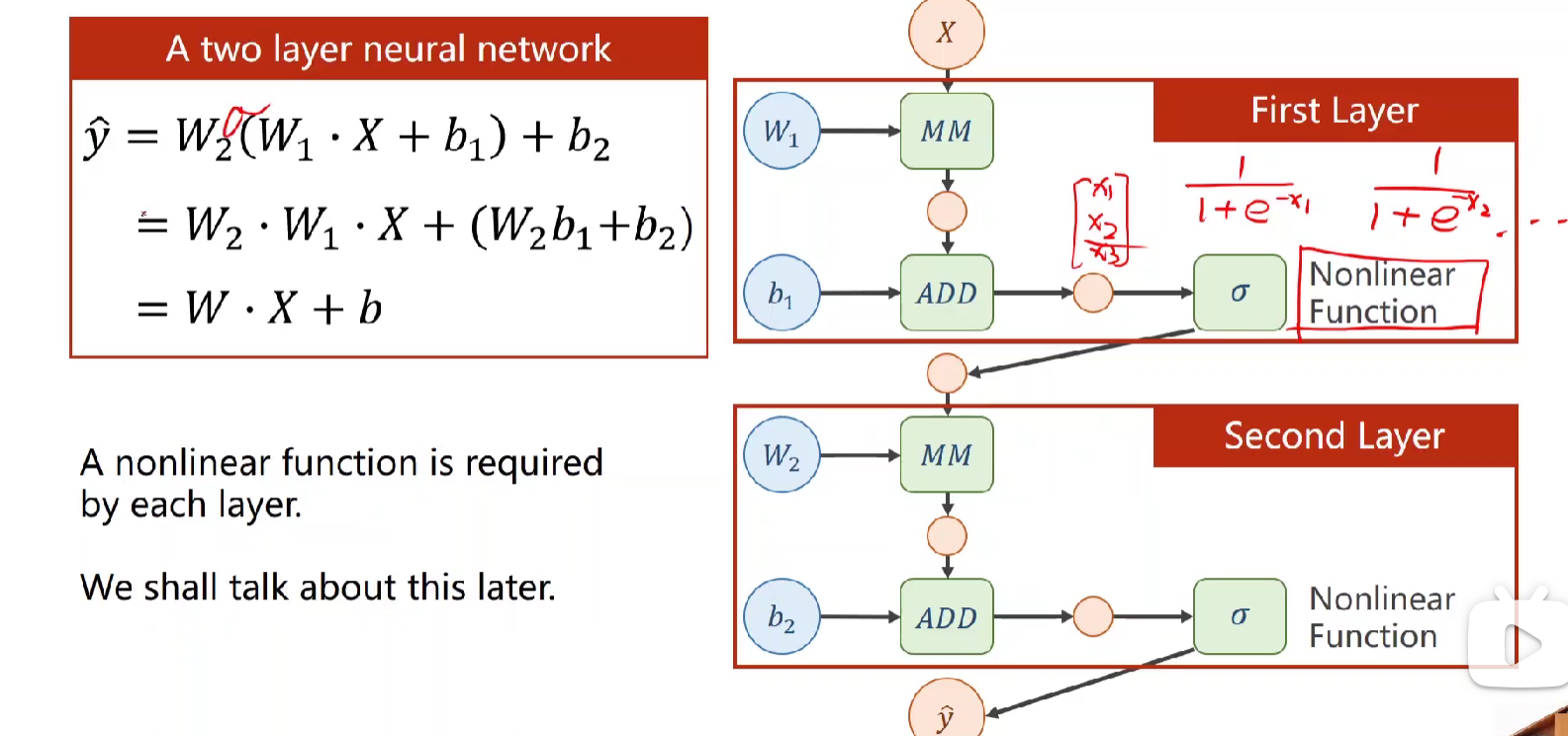
但其实上述式子化简完本质上也是 Wx+b, 只是化简完难以计算无意义。

-->改进：因此为了让式子无法展开，一般会通过非线性变换函数，即激活函数。

---

 

前馈计算foreward  &  反向传播backward

 1.前馈计算（蓝色部分）：x、w通过f（x,w)可以算出z，并继续向前得到 loss。

在向前的计算中，在f（x,w)计算模块（绿色）会计算局部梯度并保存（在pytorch中会保留至变量x、w中），用于后续反向传播。

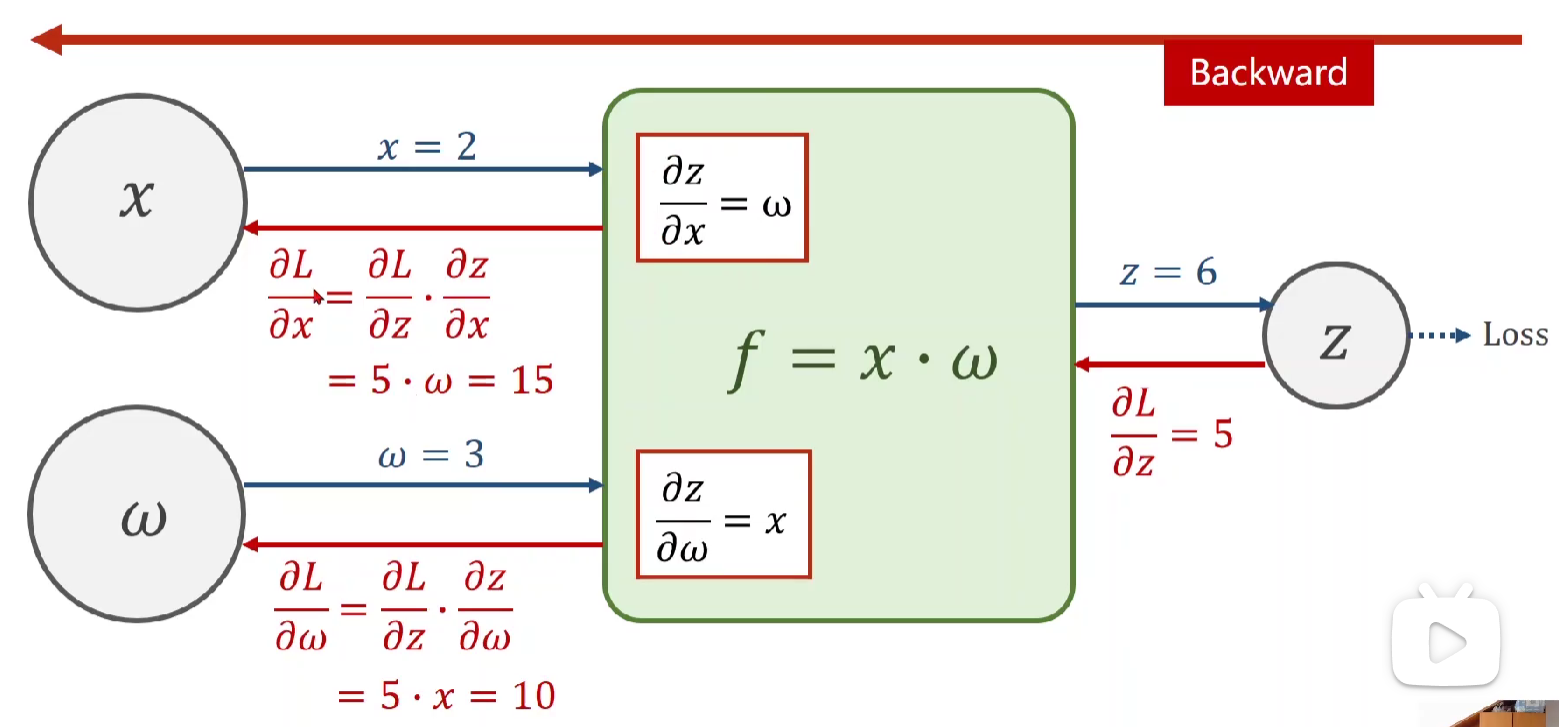
 2.反向传播（红色部分）：如图所示，后面的神经元会将loss的导数传回来，然后与f中保留的导数相乘，即有链式法则，得到 loss对x、w的偏导。

若x不是输入的，而是上一层得到的，则下一步操作中x就是此刻的z，我们已知了 loss对x的偏导，可用求上一层神经元的偏导。

 以下为举例，也可翻看作业习题

---

---

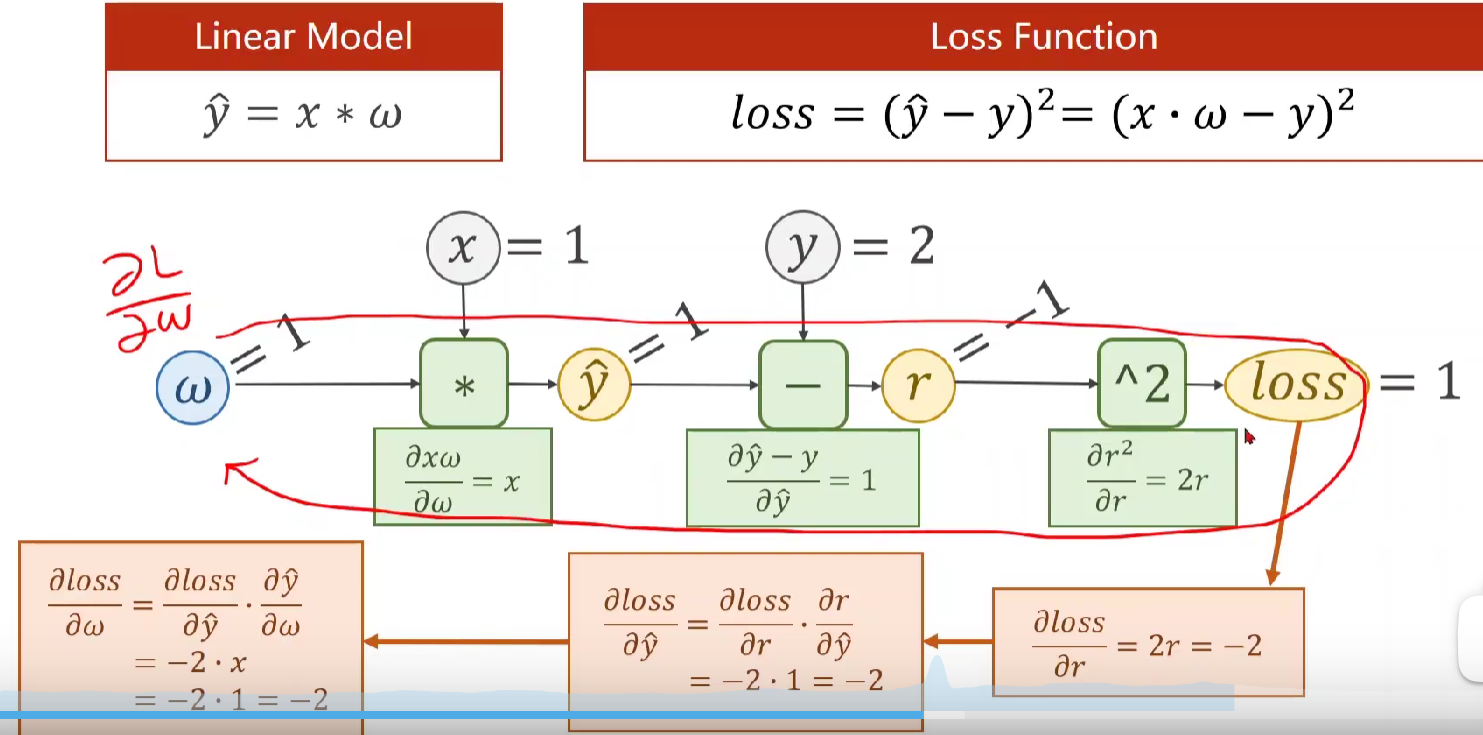
Tenser：pytorch中最基本的数据成员，保存所有数据，包括data，grad

 定义tensor则可以构建如上图的计算图。用pytorch构建模型时本质上就是在构建这样的计算图。

代码如下：

import torch

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = torch.Tensor([1.0])#中括号
w.requires_grad = True#需要计算梯度！！！

def forward(x):
    return x*w    
#因为在这里w为tensor类型，所以x也会自动转化为tensor，得到的值也要进行梯度计算

def loss(x,y):  #调用一次loss，本质上就是构建一个计算图
    y_pred = forward(x)
    return (y_pred-y)**2

#此时forward传回来是张量，要用item来取标量，而不是输出计算图
print("predict(before training)",4,forward(4).item())   

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        l = loss(x,y)#先算损失
        l.backward() #再反向传播
        print('\tgrad:',x,y,w.grad.item())
        w.data = w.data - 0.01*w.grad.data

        w.grad.data.zero_() #对这一次的梯度清零，不然下一次会加上该导数

    print("Epoch",epoch,l.item())
print("predict(after training):","w=4",w.data.item(),forward(4).item())

 

课后作业：

这里用了两种方法，一个是梯度下降，一个是随机梯度下降

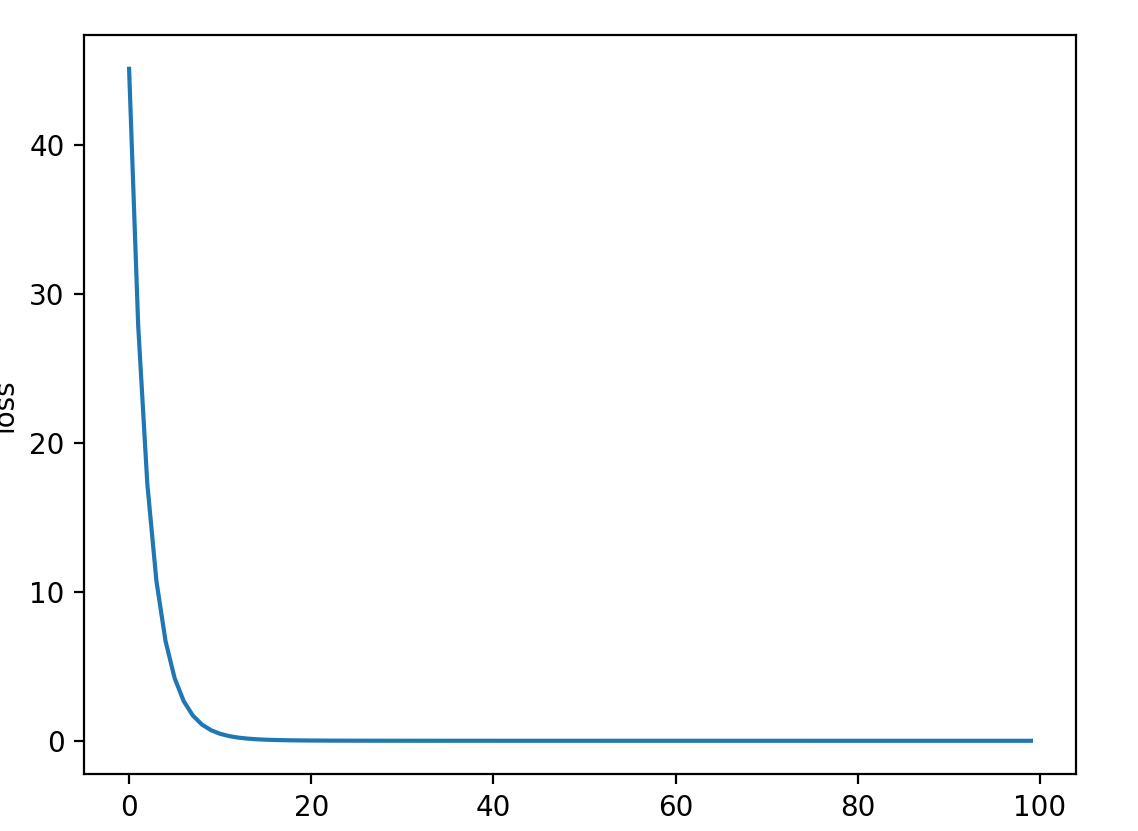
import numpy as up
import torch
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w1 = torch.Tensor([1.0])#构建计算图
w1.requires_grad = True
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True
def forward(x):#表达式要写对啊要写对！！！
    return (w1*x**2 + w2*x +b)

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y)**2

mse_list = []
epoch_list = []

for epoch in range(100):
    # cost=0       这个方法是梯度下降（均值）
    for x,y in zip(x_data,y_data):
        l = loss(x,y)
        l.backward()
        print("\tgrad",x,y,'w1:',w1.grad.item(),'w2:',w2.grad.item(),'b:',b.grad.item())
        # cost += l.item()
        w1.data = w1.data - 0.001*w1.grad.data
        w2.data = w2.data - 0.001*w2.grad.data
        b.data = b.data - 0.001*b.grad.data
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_()
    # mse_list.append(cost/len(x_data))     梯度下降
    mse_list.append(l.item())               #这是随机梯度下降（单一）
    epoch_list.append(epoch)
    print("Eporch:",epoch,l.item())
print("predict(atfer training):",4,forward(4).item())

plt.plot(mse_list)
plt.xlabel('Epoch')
plt.ylabel('loss')
plt.show()