单目相机标定理论
参考:
[相机标定之张正友标定法数学原理详解(含python源码)]: https://zhuanlan.zhihu.com/p/94244568
[相机小孔成像模型(逐步推导详解)]: https://blog.csdn.net/qq_46058802/article/details/126227358
[计算机视觉之--- 相机畸变]: https://zhuanlan.zhihu.com/p/668614140
小孔成像
- 没有镜头
- 小光圈
- 倒立的实像
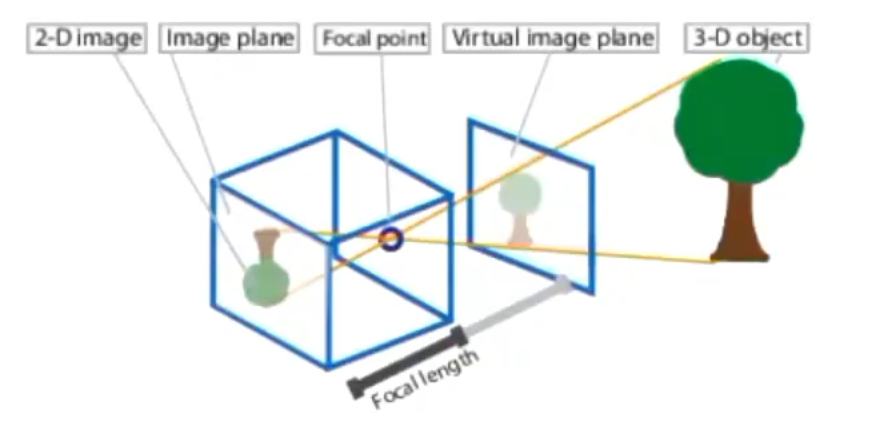
坐标系介绍
-
世界坐标系
物理世界真实的点坐标
\[\left[\begin{matrix}x_w\\y_w\\z_w\\1\end{matrix}\right]
\]
-
相机坐标系
原点位于光心处
\[\left[\begin{matrix}x_c\\y_c\\z_c\\1\end{matrix}\right]
\]
-
图像坐标系
像平面坐标系,原点在图像的中心
\[\left[\begin{matrix}x\\y\\1\end{matrix}\right]
\]
-
像素坐标系
转换为数字图像,单位为pixel,原点在左上角
\[\left[\begin{matrix}u\\v\\1\end{matrix}\right]
\]
坐标系转换
物理世界坐标系的点如何映射到像素的点
\[P_w->P_c->P_i->P
\]
世界坐标系到相机坐标系
同为物理世界的三维点,由于坐标系的不同而发生了坐标值的转换,在空间上体现的是旋转+平移
\[P_c=\left[\begin{matrix}x_c\\y_c\\z_c\\1\end{matrix}\right]=\left[\begin{matrix}R&T\\0&1\end{matrix}\right]\left[\begin{matrix}x_w\\y_w\\z_w\\1\end{matrix}\right]=\left[\begin{matrix}R&T\\0&1\end{matrix}\right]P_w
\]
R为旋转矩阵
-
绕x轴旋转
x值不变
\[R_x(\phi)=\left[\begin{matrix}1&0&0\\0&cos\phi&-sin\phi\\0&sin\phi&cos\phi\end{matrix}\right]
\]

-
绕y轴旋转
y值不变
\[R_y(\theta)=\left[\begin{matrix}cos\theta&0&sin\theta\\0&1&0\\-sin\theta&0&cos\theta\end{matrix}\right]
\]
-
绕z轴旋转
z值不变
\[R_y(\theta)=\left[\begin{matrix}cos\psi&-sin\psi&0\\sin\psi&cos\psi&0\\0&0&1\end{matrix}\right]
\]
相机坐标系到图像坐标系
真实物理世界三维点到图像平面的转换,投影变换

在xoz平面内

点P经过光心O投影到P'
\[\frac{y_c}{z_c}=\frac{y}{f}\\
y=\frac{y_c}{z_c}f
\]
在yoz平面内
\[\frac{x_c}{z_c}=\frac{x}{f}\\
x=\frac{x_c}{z_c}f
\]
转换为矩阵形式:
\[P'=\left[\begin{matrix}x\\y\end{matrix}\right]=\frac{f}{z_c}\left[\begin{matrix}x_c\\y_c\end{matrix}\right]
\]
用齐次坐标表达:
\[P'=\left[\begin{matrix}x\\y\\1\end{matrix}\right]=\frac{1}{z_c}\left[\begin{matrix}f&0&0&0\\
0&f&0&0\\0&0&1 &0\end{matrix}\right] \left[\begin{matrix}x_c\\y_c\\z_c\\1\end{matrix}\right]
\]
图像坐标系到像素坐标系
实际像平面连续的坐标转换为以像素为单位的距离表示,需要进行比例缩放,同时由于图像坐标系和像素坐标系的原点不同,还有一个位置偏移,像素坐标系是以左上角的像素点作为原点。
x,y,z的单位为距离mm
u,v的单位为像素pixel
mm->pixel
比例系数为k(pixel/mm)
传感器的像元尺寸为长宽dx,dy其单位为mm/pixel
传感器的分辨率的一半为u0,v0,单位为pixel
\[P'=\left[\begin{matrix}u\\v\\1\end{matrix}\right]=\left[\begin{matrix}\frac{1}{dx}&0&u_0\\
0&\frac{1}{dy}&v_0\\0&0&1 \end{matrix}\right] \left[\begin{matrix}x\\y\\1\end{matrix}\right]
\]
世界坐标系到像素坐标系(完)
\[z_c\left[\begin{matrix}u\\v\\1\end{matrix}\right]=
\left[\begin{matrix}\frac{1}{dx}&0&u_0\\0&\frac{1}{dy}&v_0\\0&0&1\end{matrix}\right]
\left[\begin{matrix}f&0&0&0\\
0&f&0&0\\0&0&1 &0\end{matrix}\right]
\left[\begin{matrix}R&T\\0&1\end{matrix}\right]
\left[\begin{matrix}x_w\\y_w\\z_w\\1\end{matrix}\right]
\]
相机畸变
在了解相机畸变前,以上为针孔相机成像模型,相机通过小孔成像,光线通过小孔(光圈)进入相机内部到达传感器平面
目前高性能手机的像素有的超过了专业相机,但是相机成像的效果却比手机更具细节,是因为相机拥有更大尺寸的传感器和更大的光圈,这使得单个像元获得光更多,更具有表达能力。
而对于针孔模型而言,光圈变大意味着小孔变大,会有多个不同点的光线到达像平面的同一个点上,导致图像模糊,而小光圈会导致图像的解析能力不够,图像很暗。
为了使得光圈变大,图像清晰又具有细节,需要将同一个点散发的多个光线同时汇聚在一起,增加亮度,于是引入了透镜,透镜不会改变小孔成像模型
径向畸变
由透镜形状引起的畸变称之为径向畸变,图像像素点以畸变中心为中心点,沿着径向产生位置方向的偏差,导致发送形变
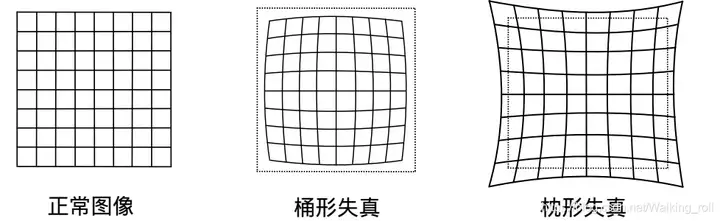
枕形畸变
畸变后的像点相对于理想像点向外偏移,远离中心
桶形畸变
畸变后的像点相对于理想像点向外偏移,靠近中心
畸变模型
\[\left\{\begin{array}{l}
x^{\prime}=x+\bar{x}\left(k_1 r^2+k_2 r^4+k_3 r^6\right) \\
y^{\prime}=y+\bar{y}\left(k_1 r^2+k_2 r^4+k_3 r^6\right)
\end{array}\right.
\]
切向畸变
在相机的组装过程中由于不能使得透镜和成像面严格平行也会引入切向畸变
目前相机制造工艺,该误差很小
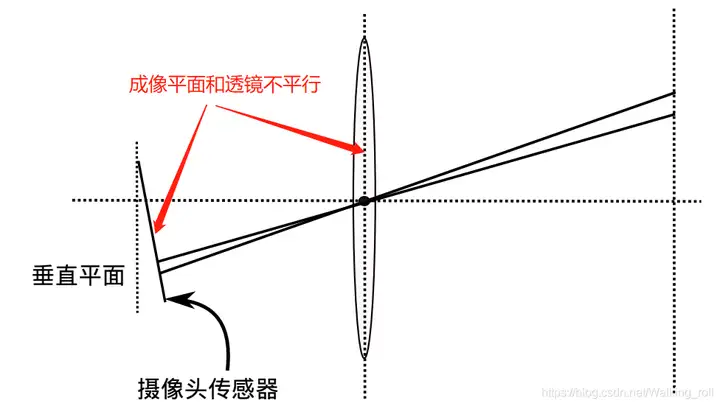
畸变模型
\[\left\{\begin{array}{l}
x^{\prime}=x+p_1\left(r^2+2 \bar{x}^2\right)+2 p_2 \bar{x} * \bar{y} \\
y^{\prime}=y+p_2\left(r^2+2 \bar{y}^2\right)+2 p_1 \bar{x} * \bar{y}
\end{array}\right.
\]
切向畸变+径向畸变模型
\[\left\{\begin{array}{l}
x^{\prime}=x+\bar{x}\left(k_1 r^2+k_2 r^4+k_3 r^6\right)+p_1\left(r^2+2 \bar{x}^2\right)+2 p_2 \bar{x} * \bar{y} \\
y^{\prime}=y+\bar{y}\left(k_1 r^2+k_2 r^4+k_3 r^6\right)+p_2\left(r^2+2 \bar{y}^2\right)+2 p_1 \bar{x} * \bar{y}
\end{array}\right.
\]
去畸变模型
\[\left\{\begin{array}{l}
x_{\text {corrected }}=x\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right)+2 p_1 x y+p_2\left(r^2+2 x^2\right) \\
y_{\text {corrected }}=y\left(1+k_1 r^2+k_2 r^4+k_3 r^6\right)+p_1\left(r^2+2 y^2\right)+2 p_2 x y
\end{array}\right.
\]
标定步骤
- 拍摄不同角度的标定板
- 角点检测
- 求解内外参矩阵
- 求解畸变参数
- 利用优化算法进行优化








 浙公网安备 33010602011771号
浙公网安备 33010602011771号