数据结构学习笔记(四)——查找
相关概念
查找 —— 在数据集合中寻找满⾜某种条件的数据元素的过程称为查找
查找表(查找结构)—— ⽤于查找的数据集合称为查找表,它由同⼀类型的数据元素(或记录)组成
关键字 —— 数据元素中唯⼀标识该元素的某个数据项的值,使⽤基于关键字的查找,查找结果应该是
唯⼀的。
静态与动态查找表
静态:一般用于只需要查找操作
动态:用于频繁插入删除操作
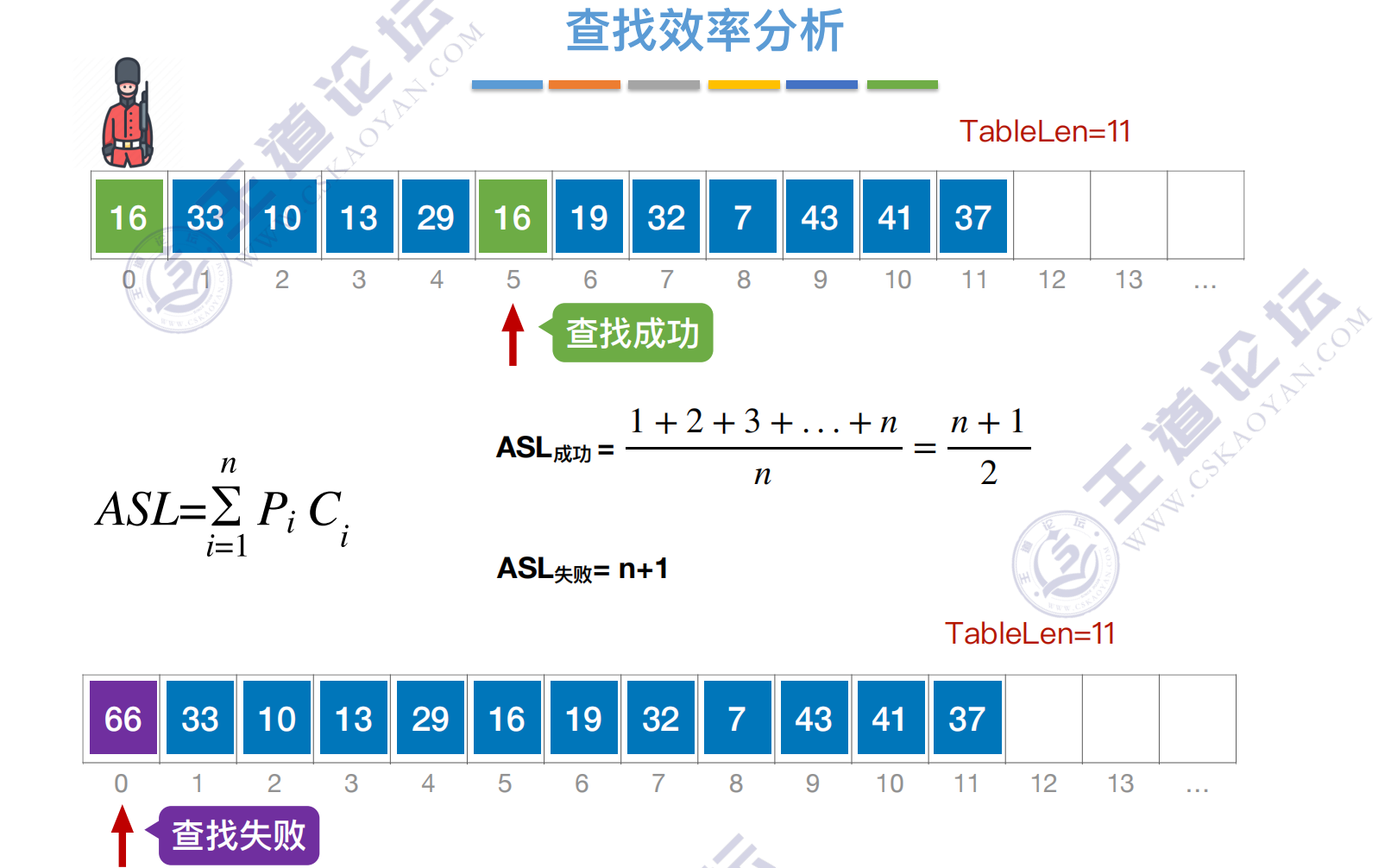
查找算法的评价指标
查找⻓度——在查找运算中,需要对⽐关键字的次数称为查找⻓度
平均查找⻓度(ASL, Average Search Length)—— 所有查找过程中进⾏关键字的⽐较次数的平均值
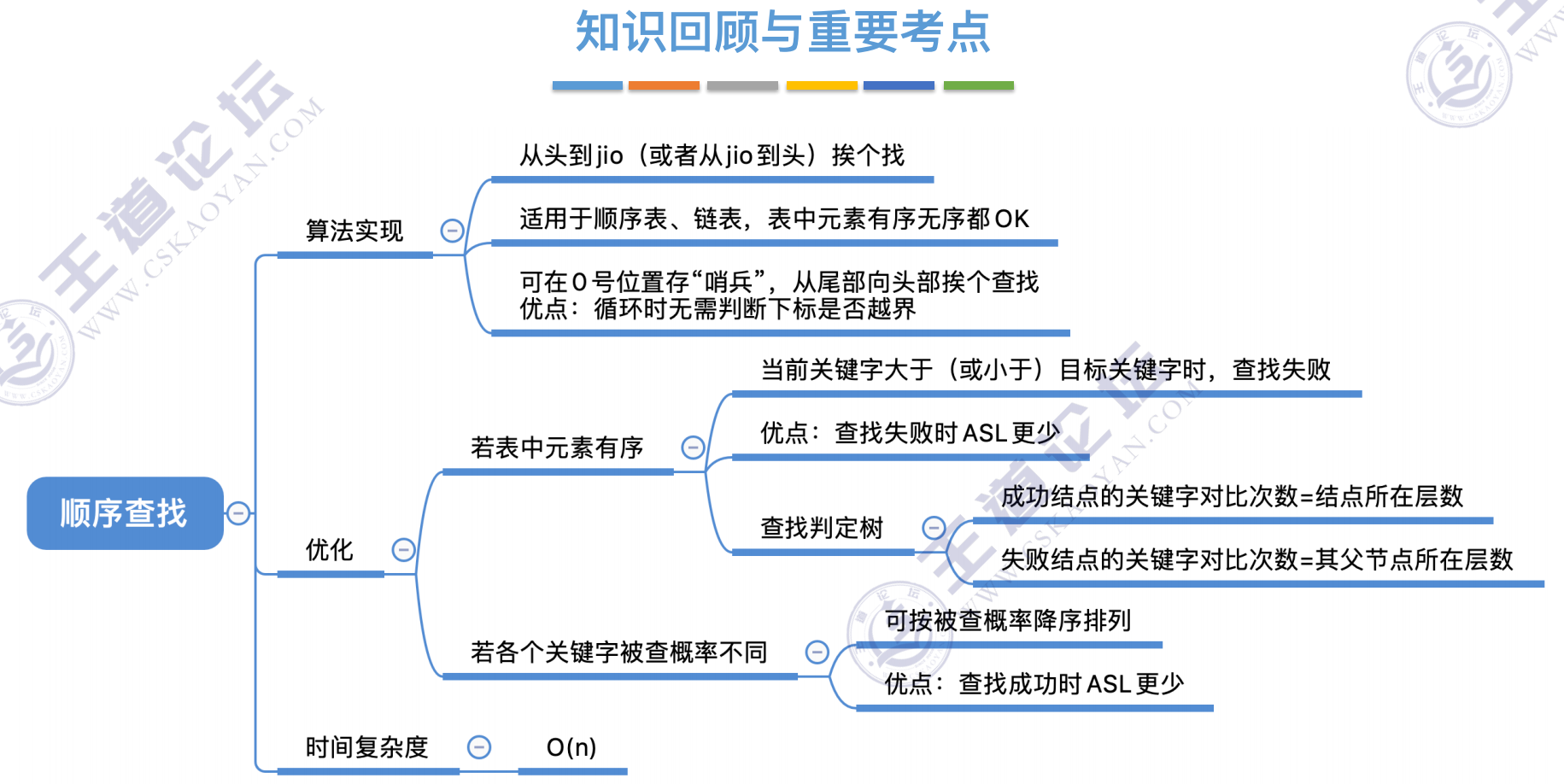
顺序查找


哨兵法:无需判断是否越界,效率相对更高
顺序查找的优化(有序表)
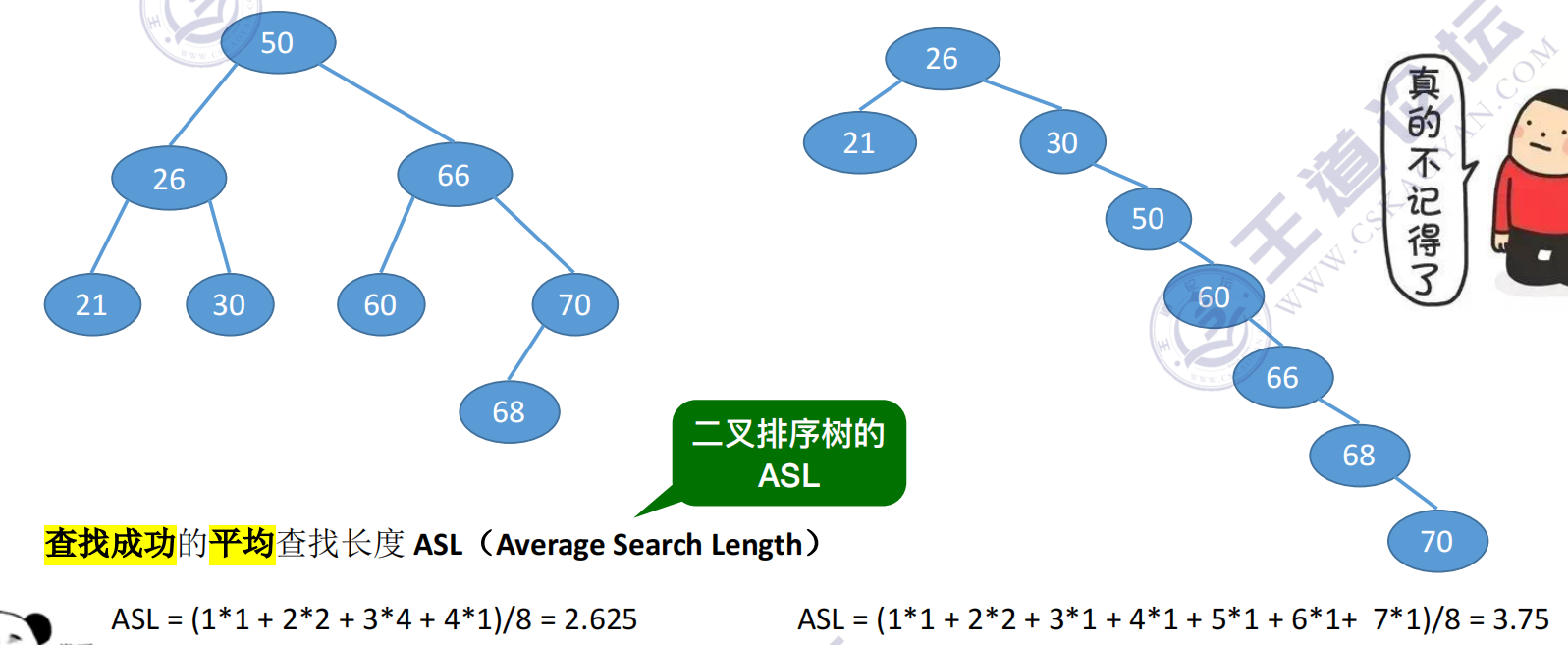
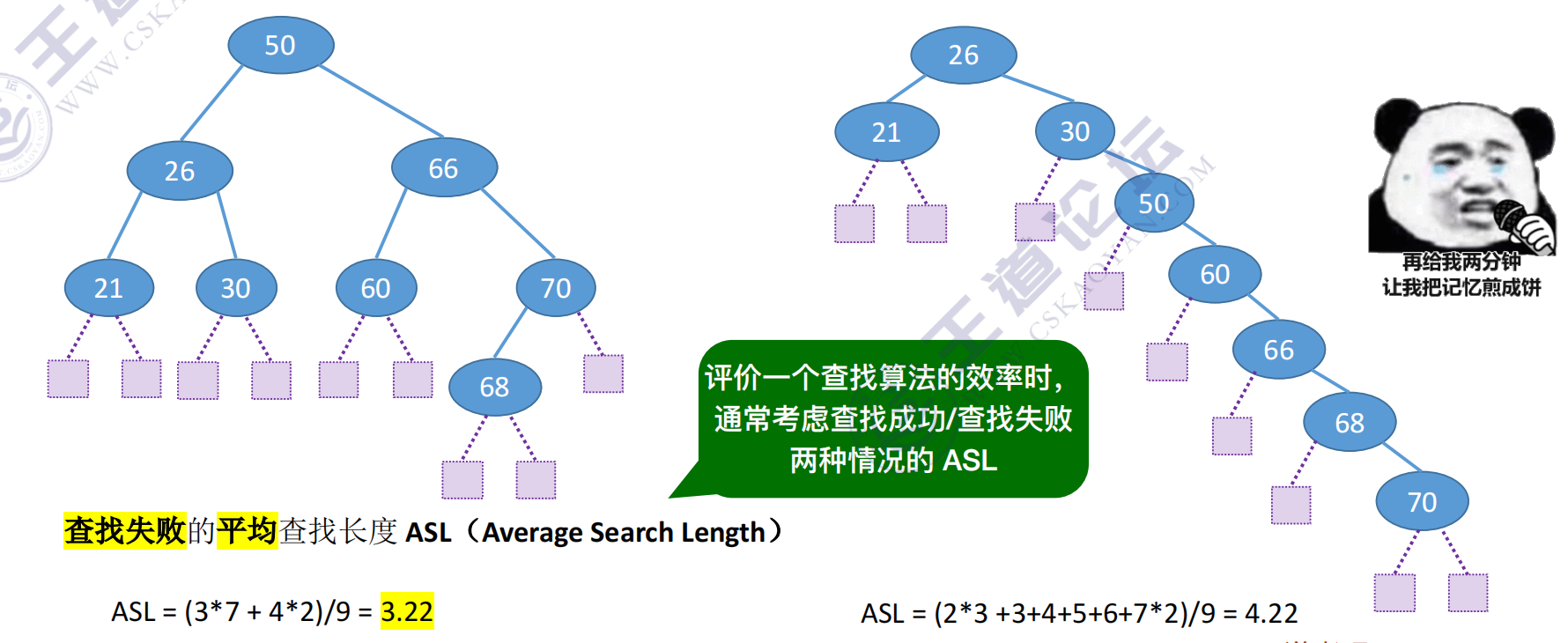
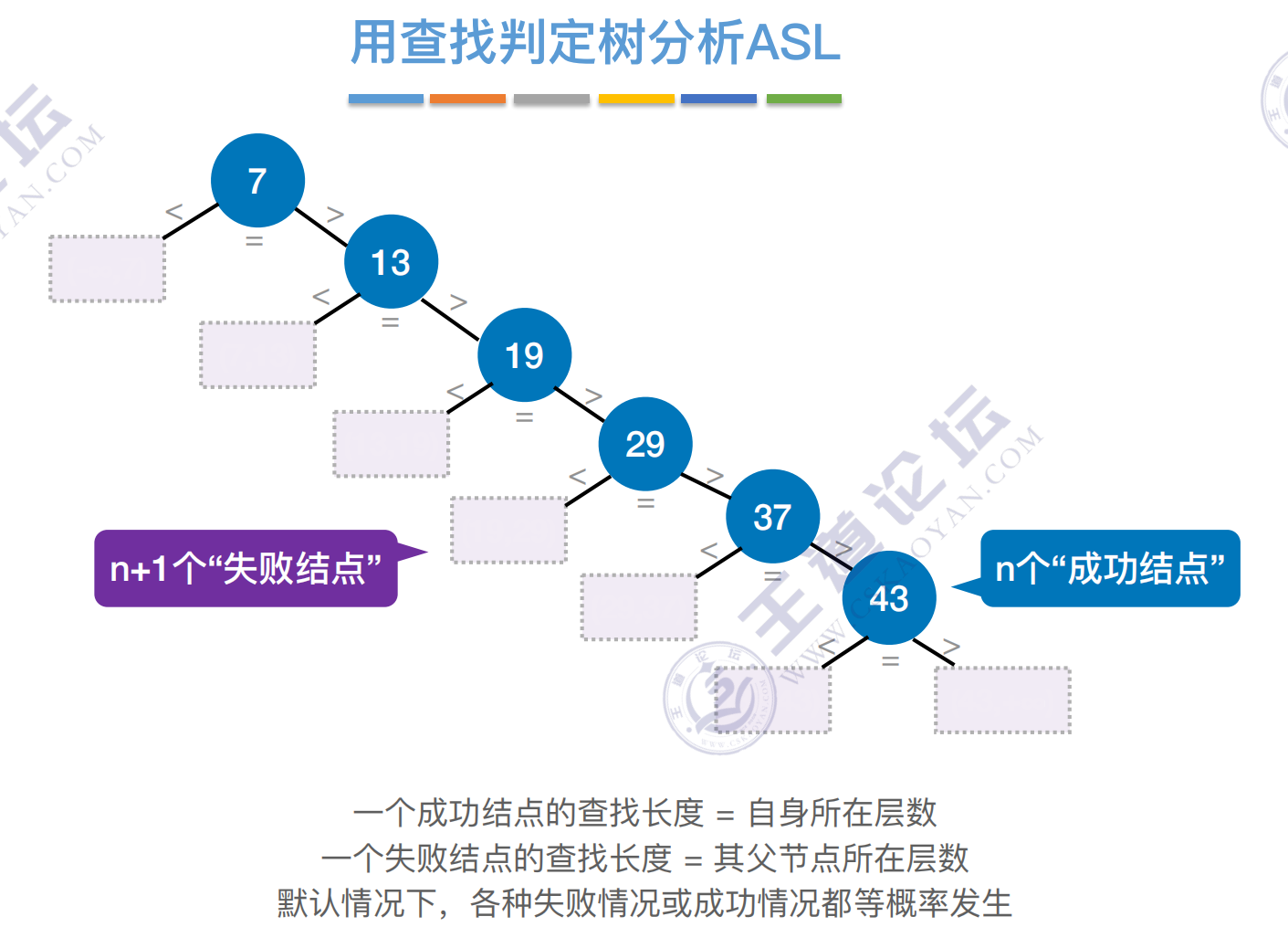
用查找判定树分析ASL
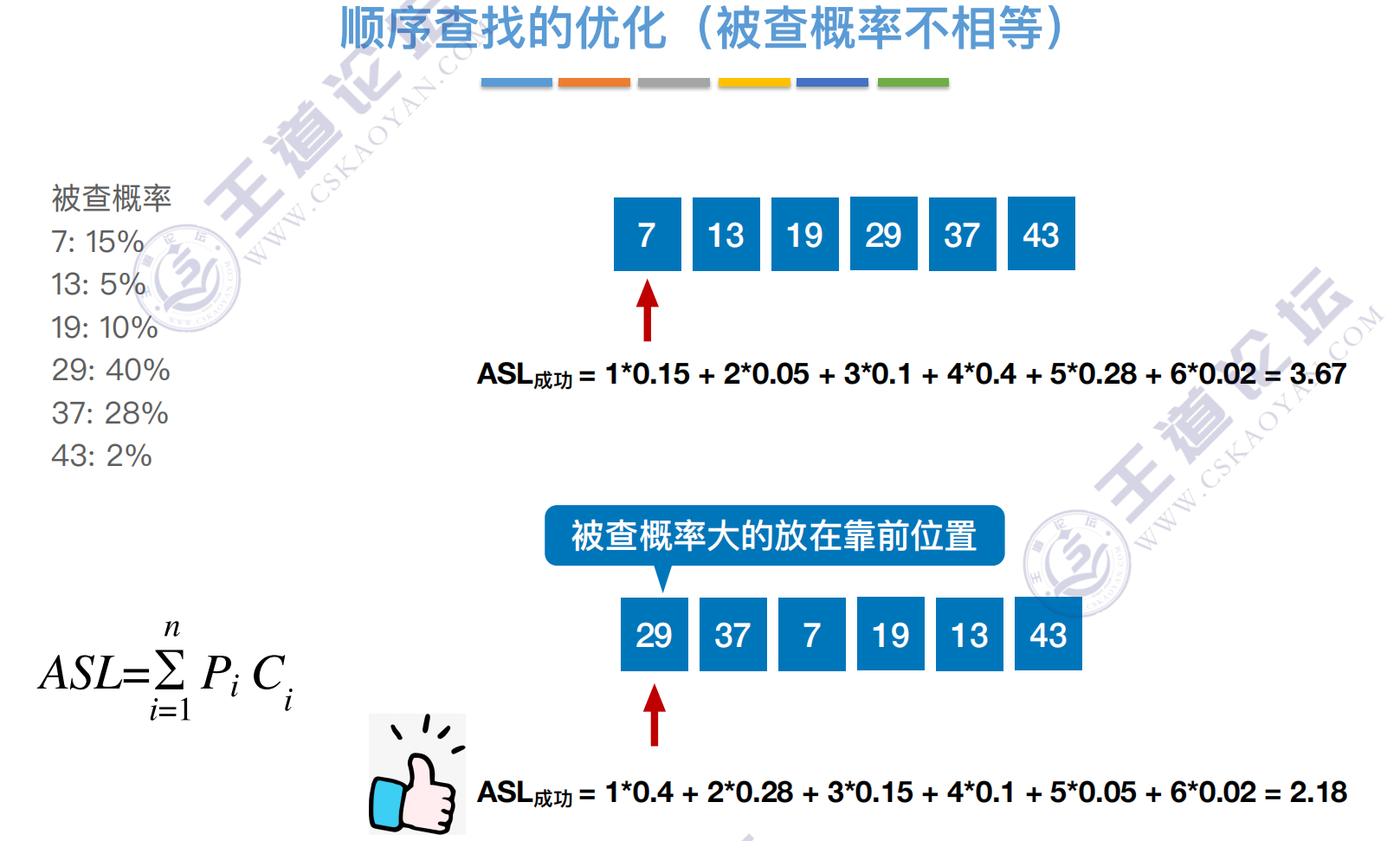
顺序查找的优化(被查概率不相等)
总结
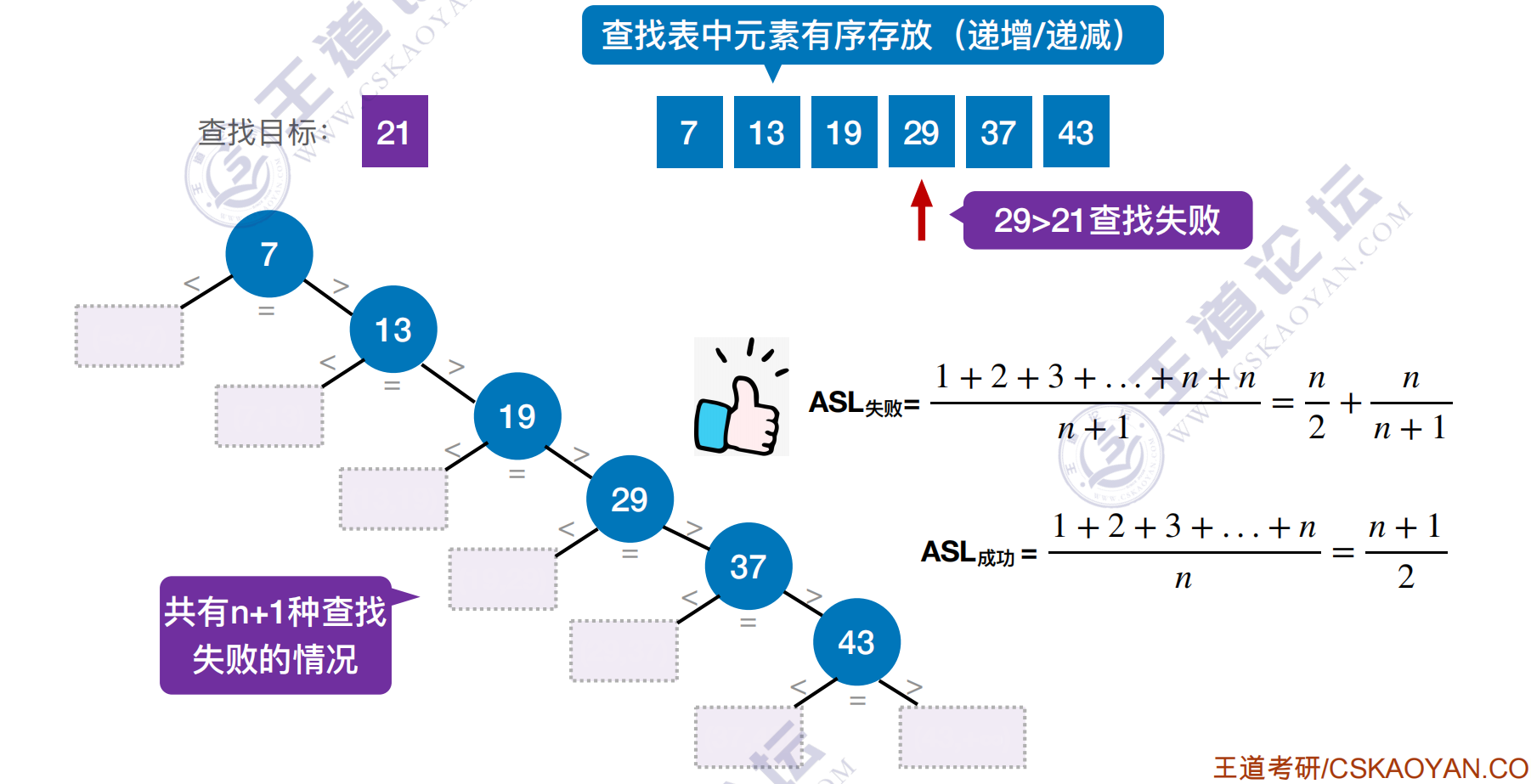
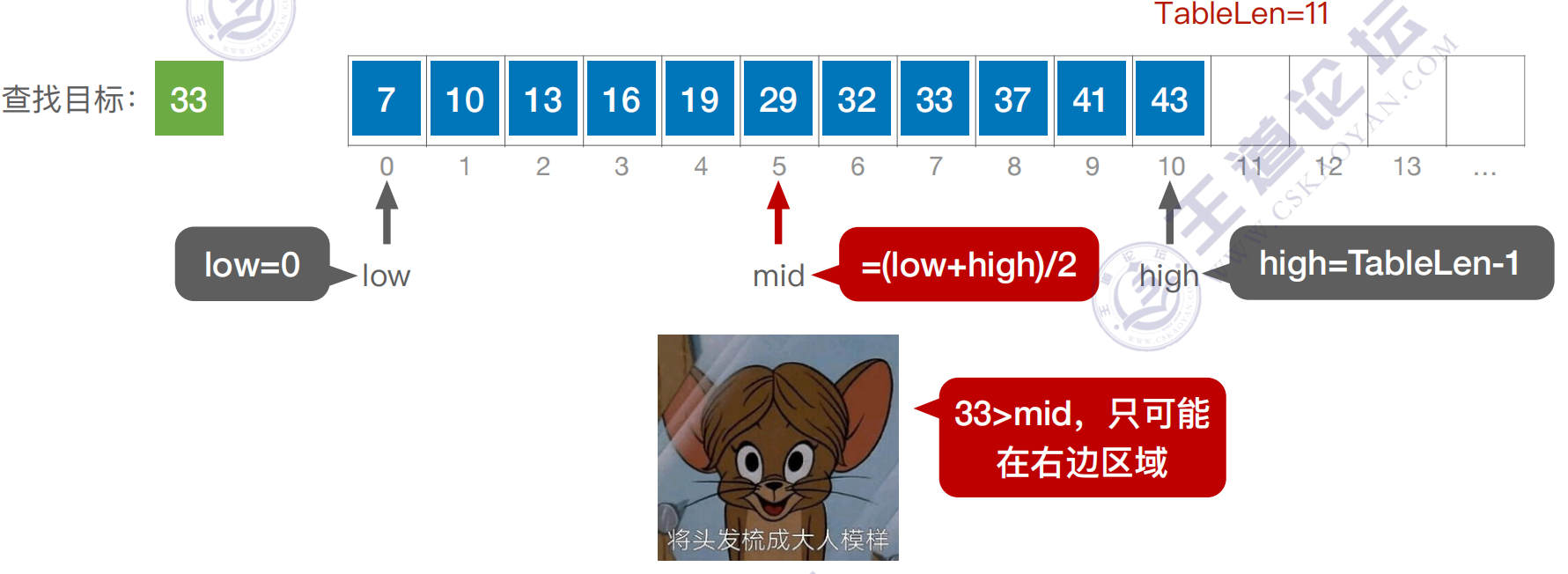
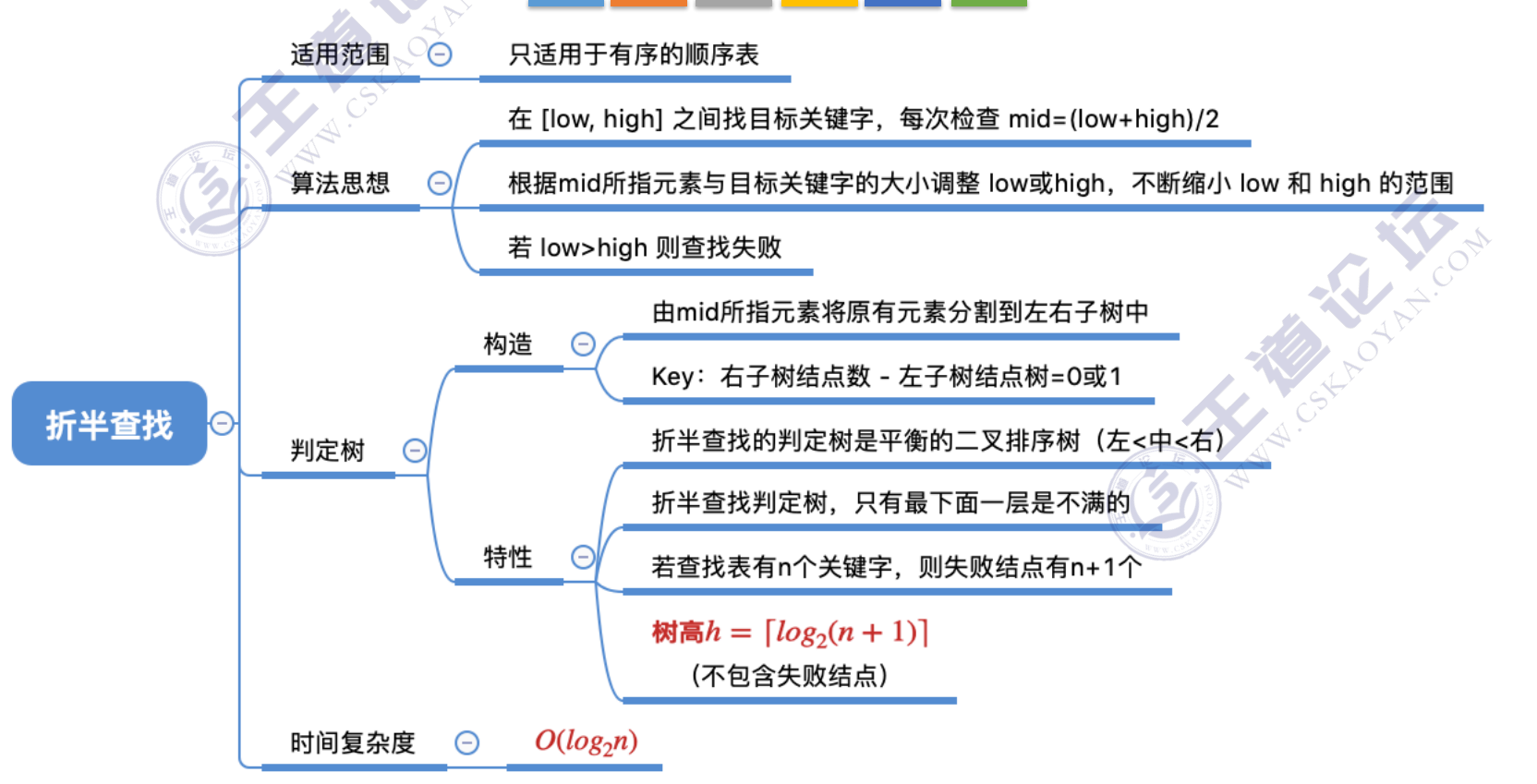
折半查找(二分查找)
折半查找,⼜称“⼆分查找”,仅适⽤于有序的顺序表。
代码实现

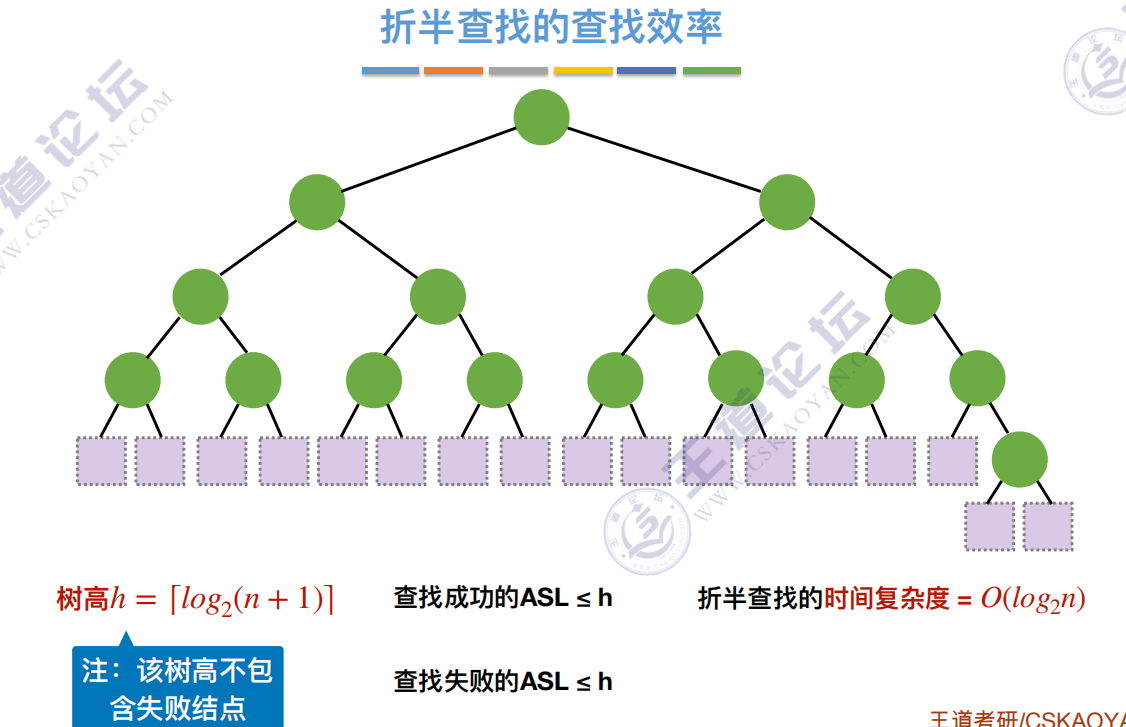
效率分析
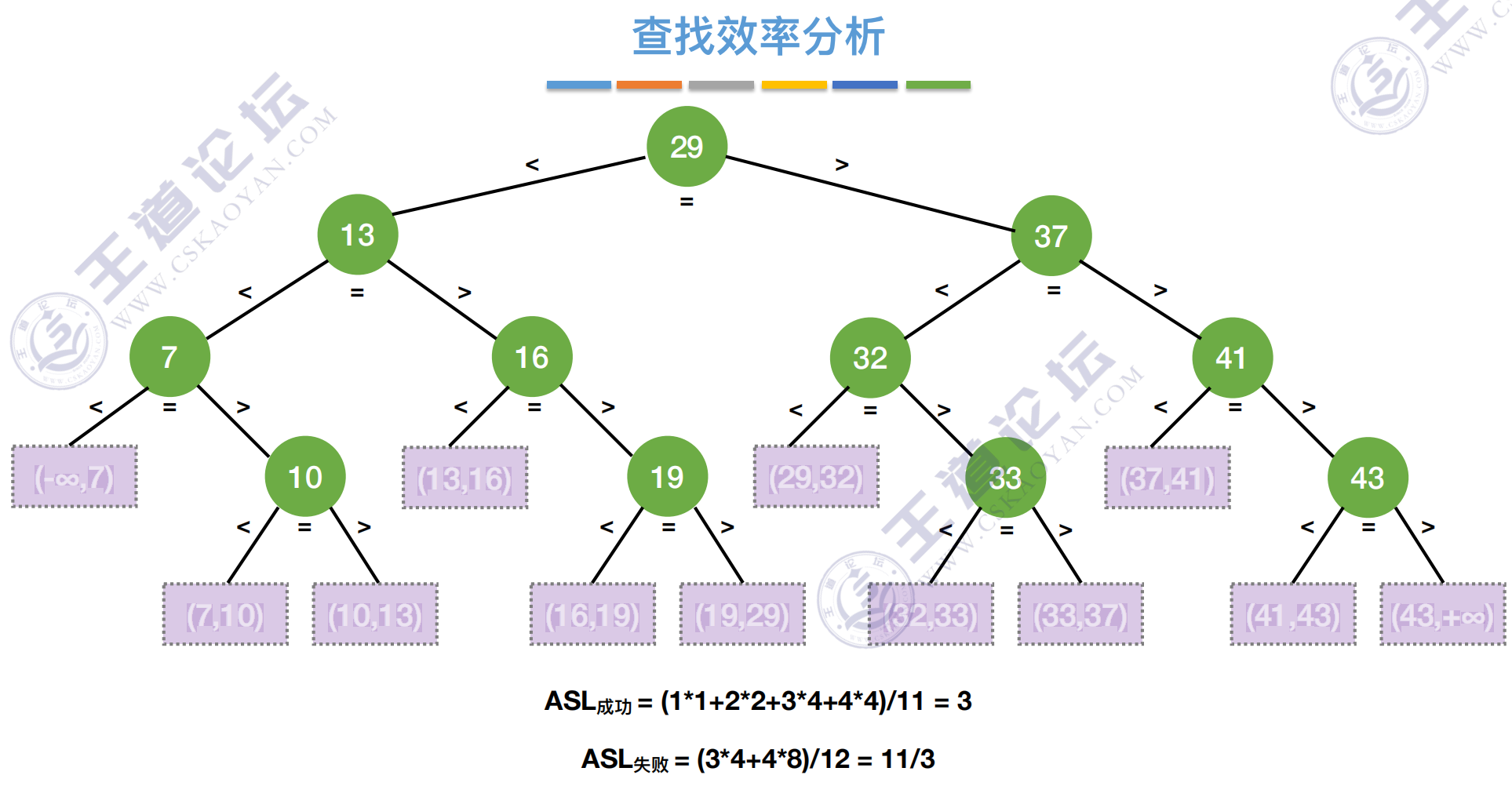
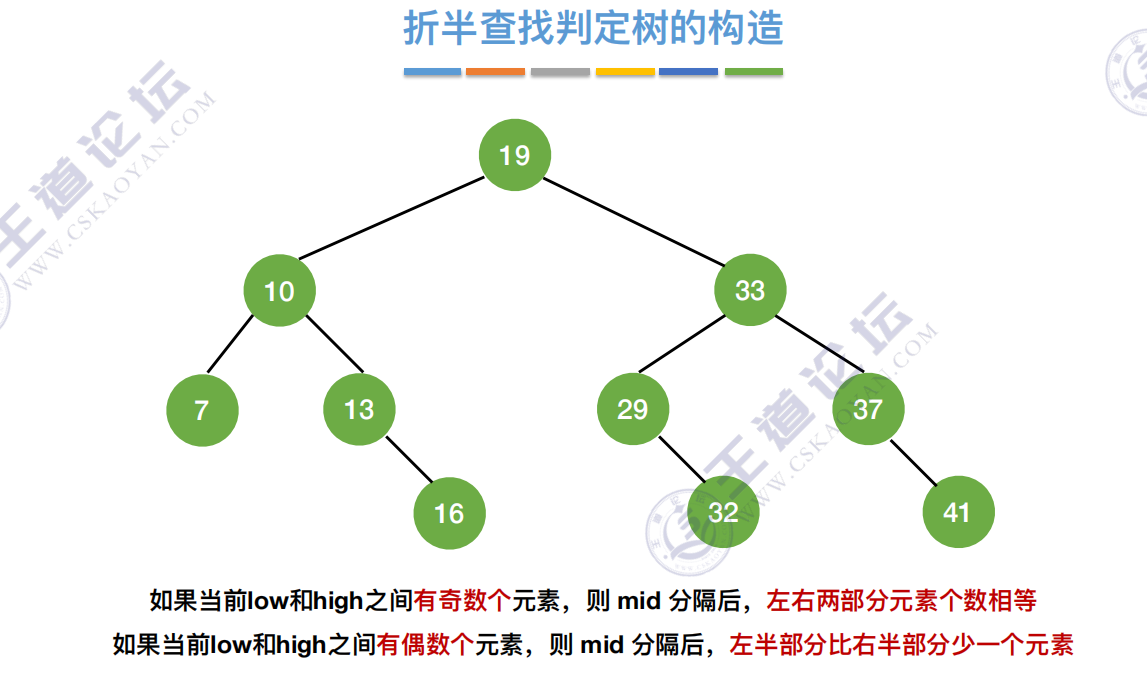
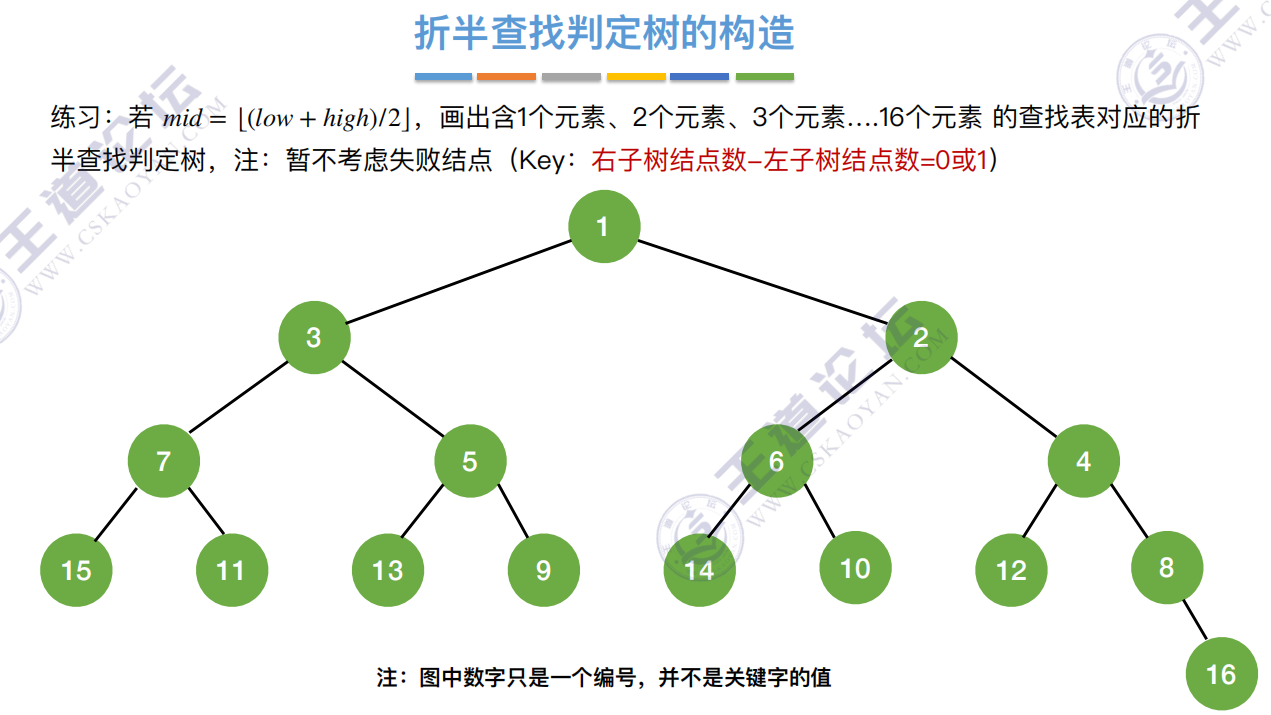
判定树构建
如果当前low和high之间有奇数个元素,则 mid 分隔后,左右两部分元素个数相等
如果当前low和high之间有偶数个元素,则 mid 分隔后,左半部分⽐右半部分少⼀个元素
平衡二叉树
总结
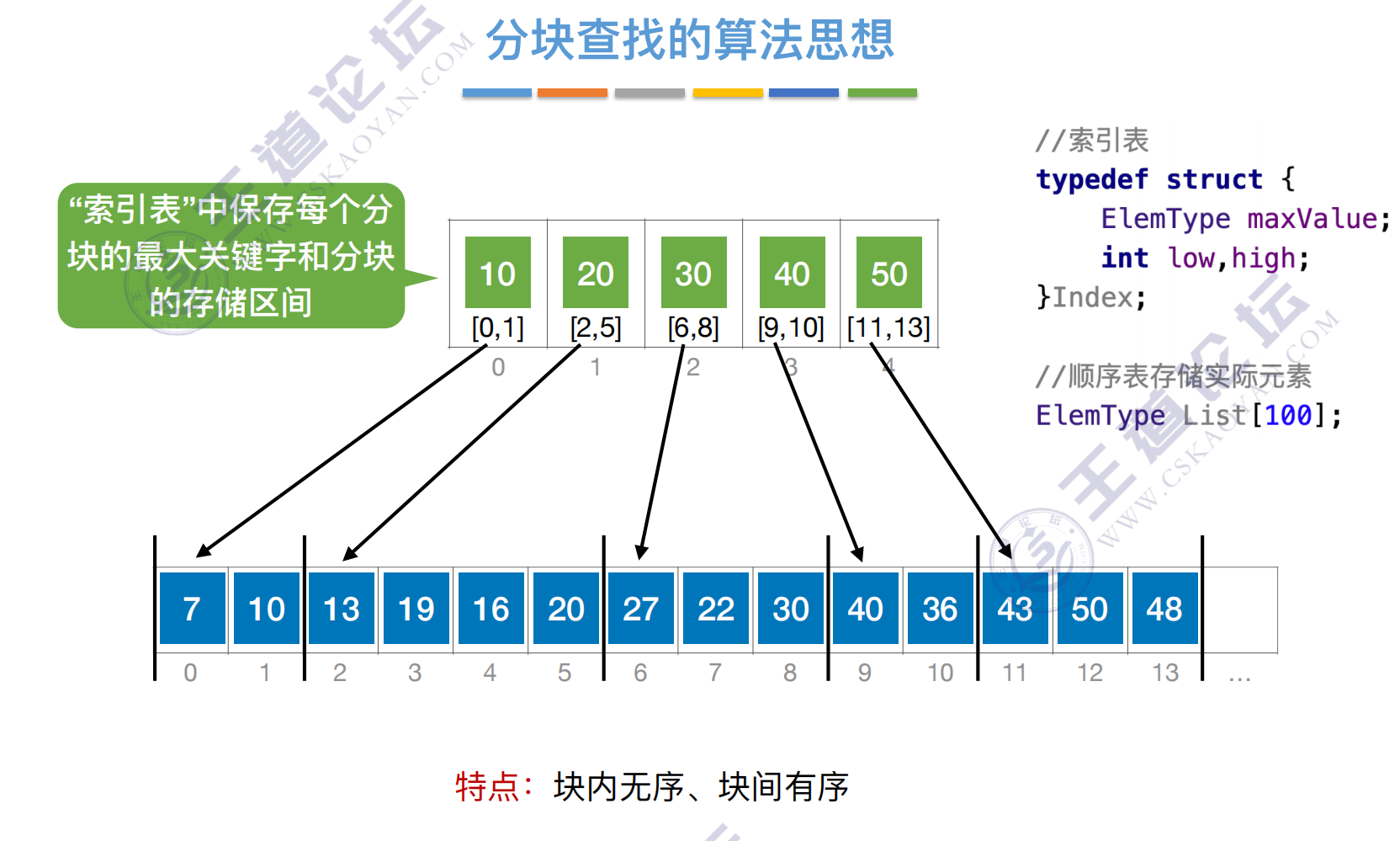
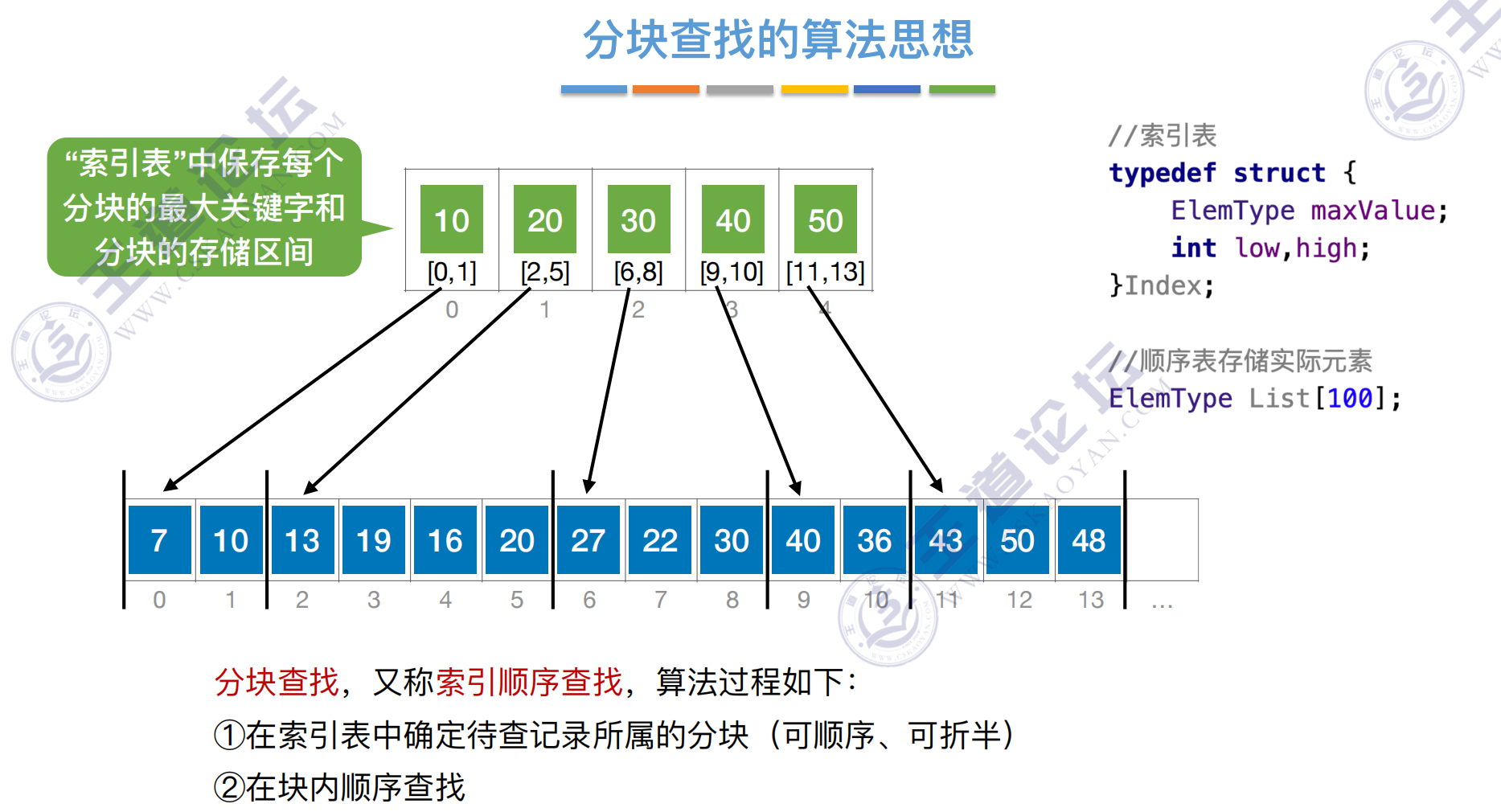
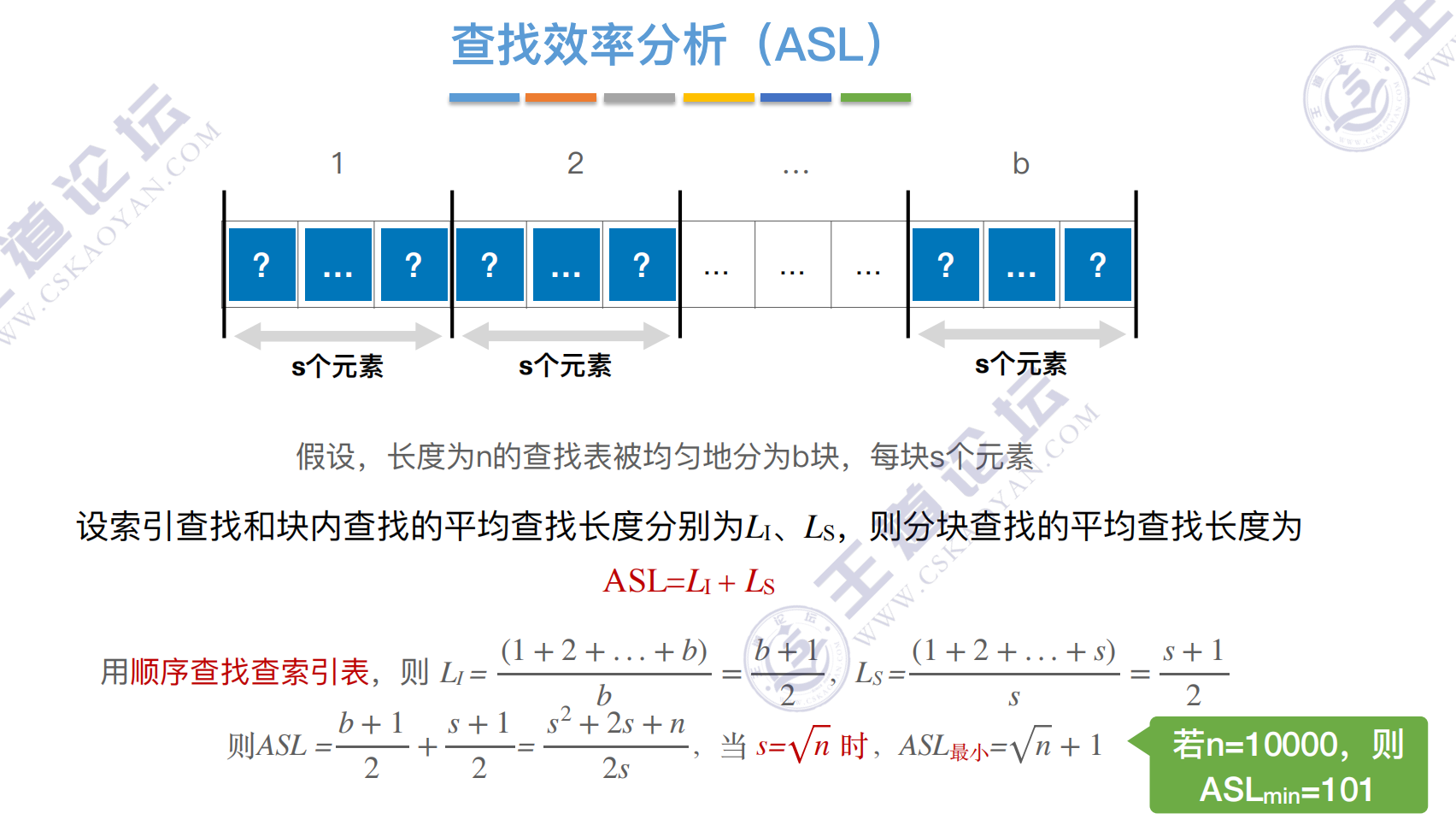
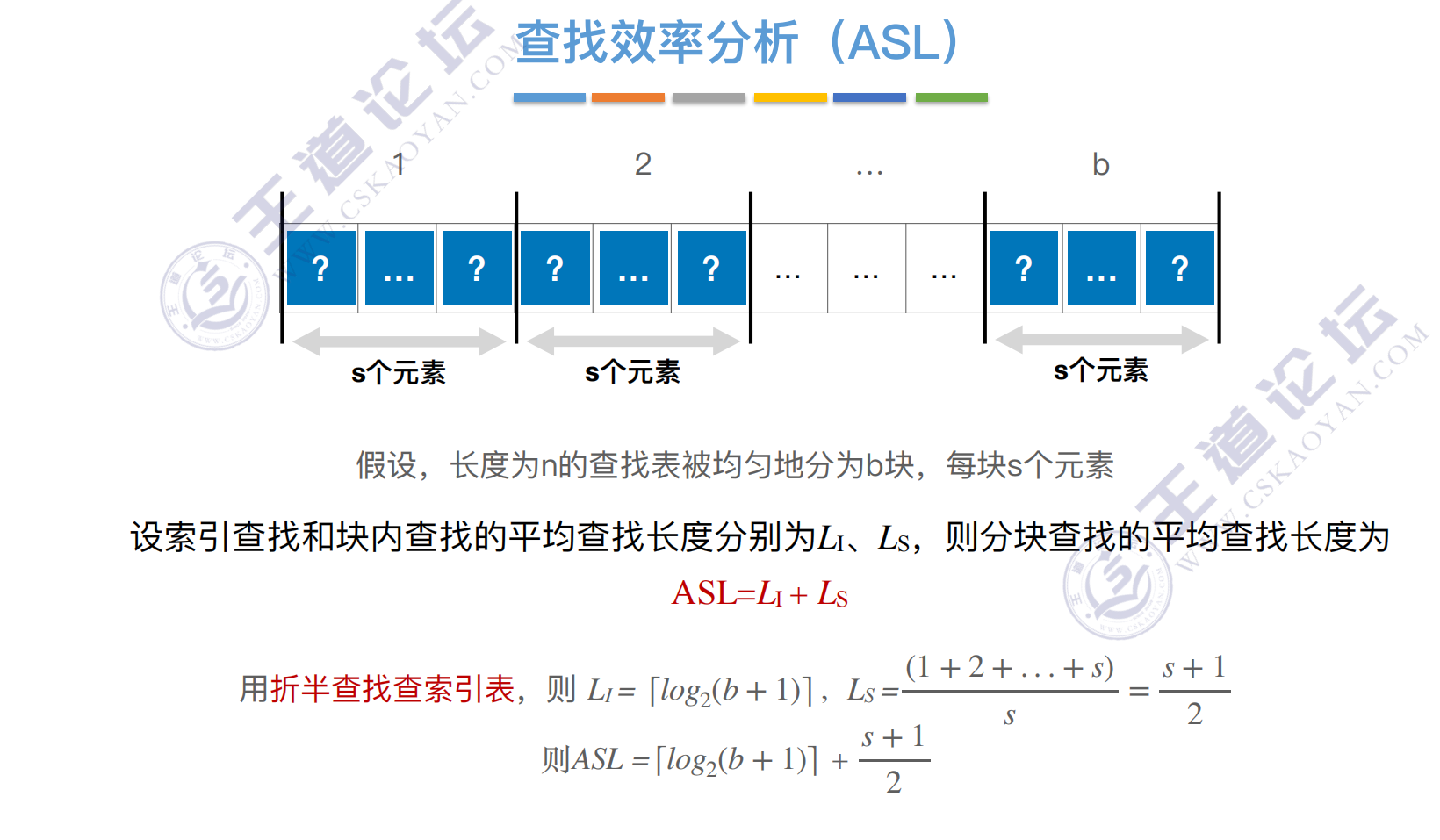
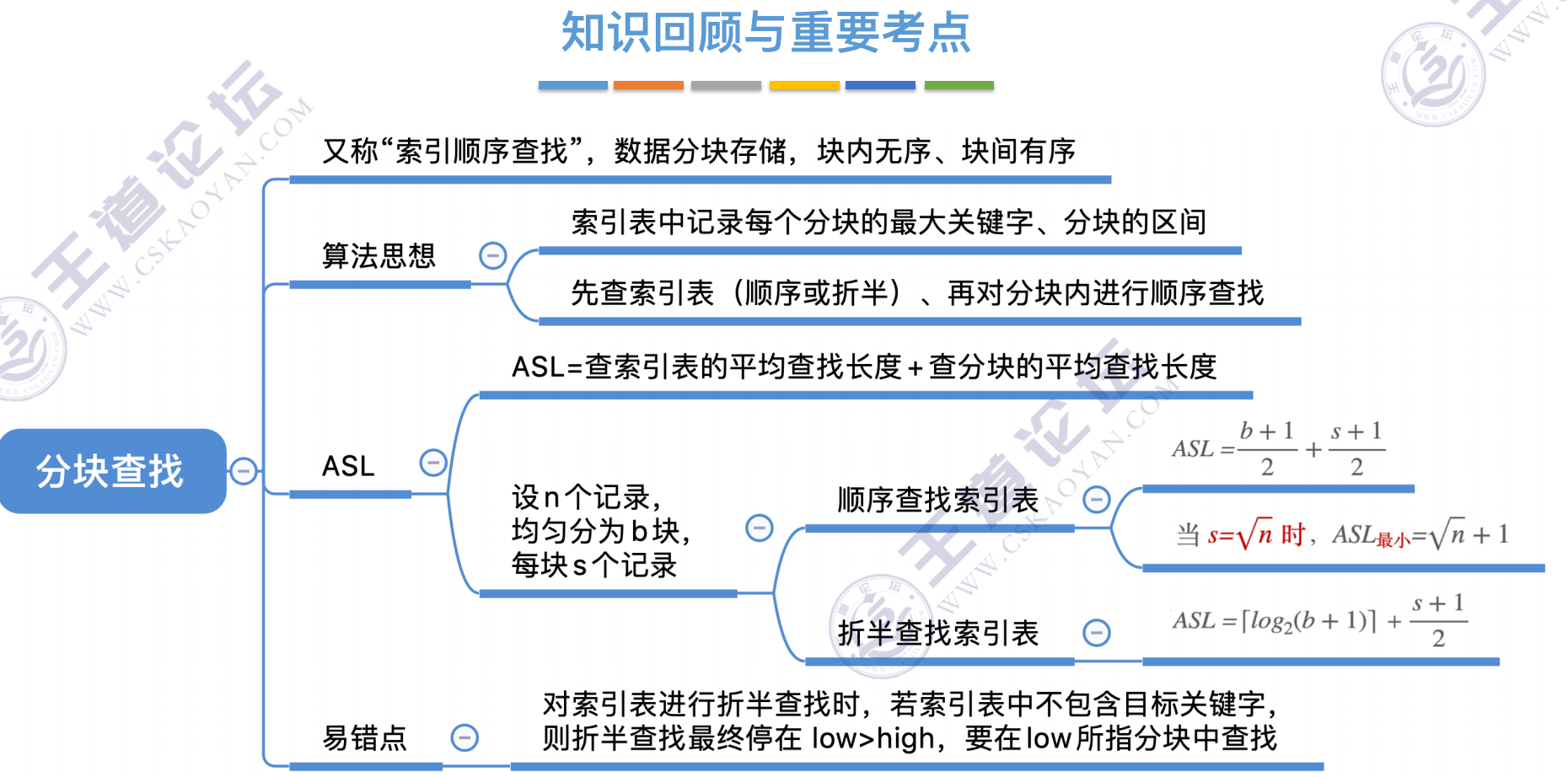
分块查找
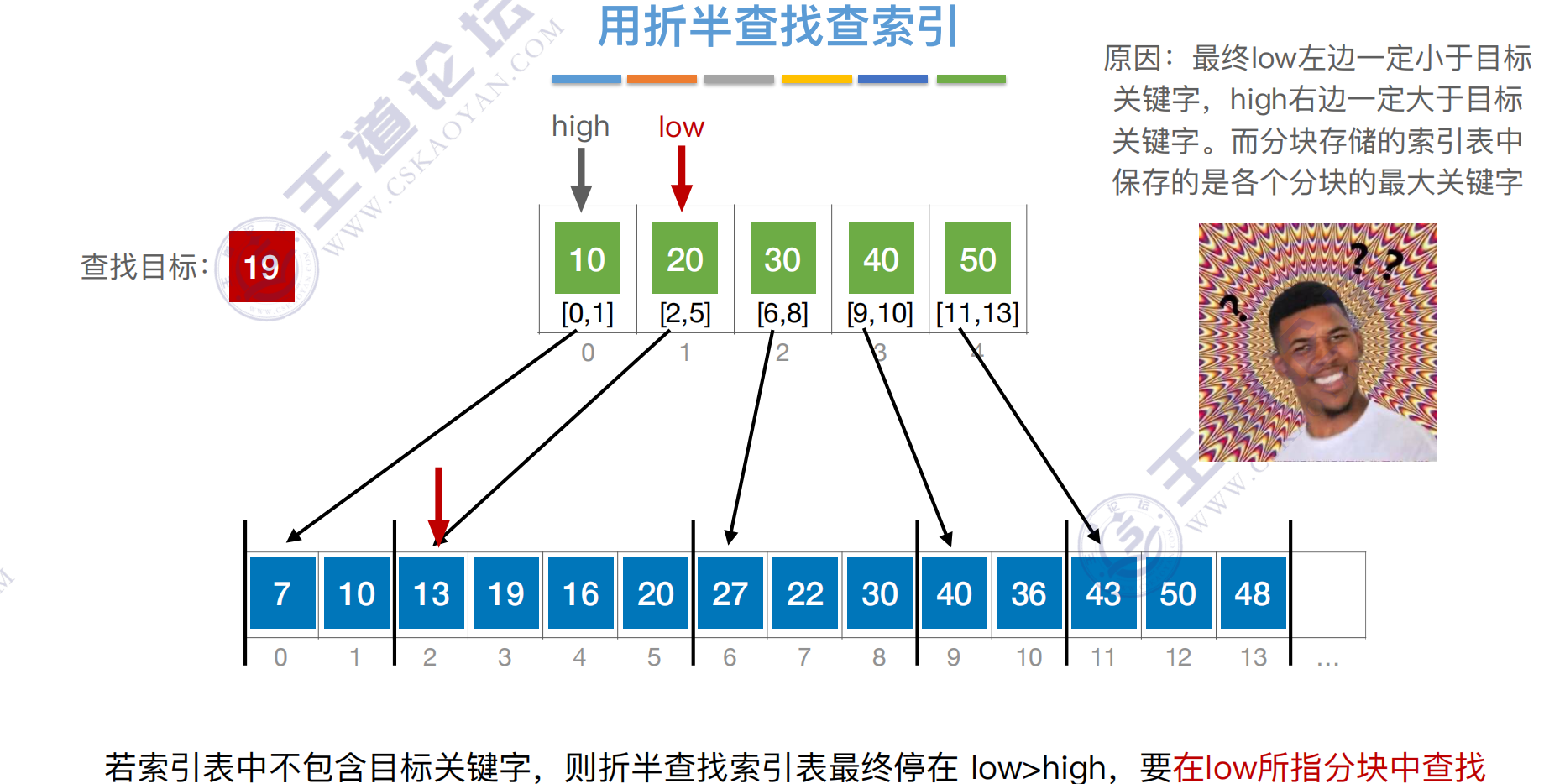
折半查找索引
效率分析
总结
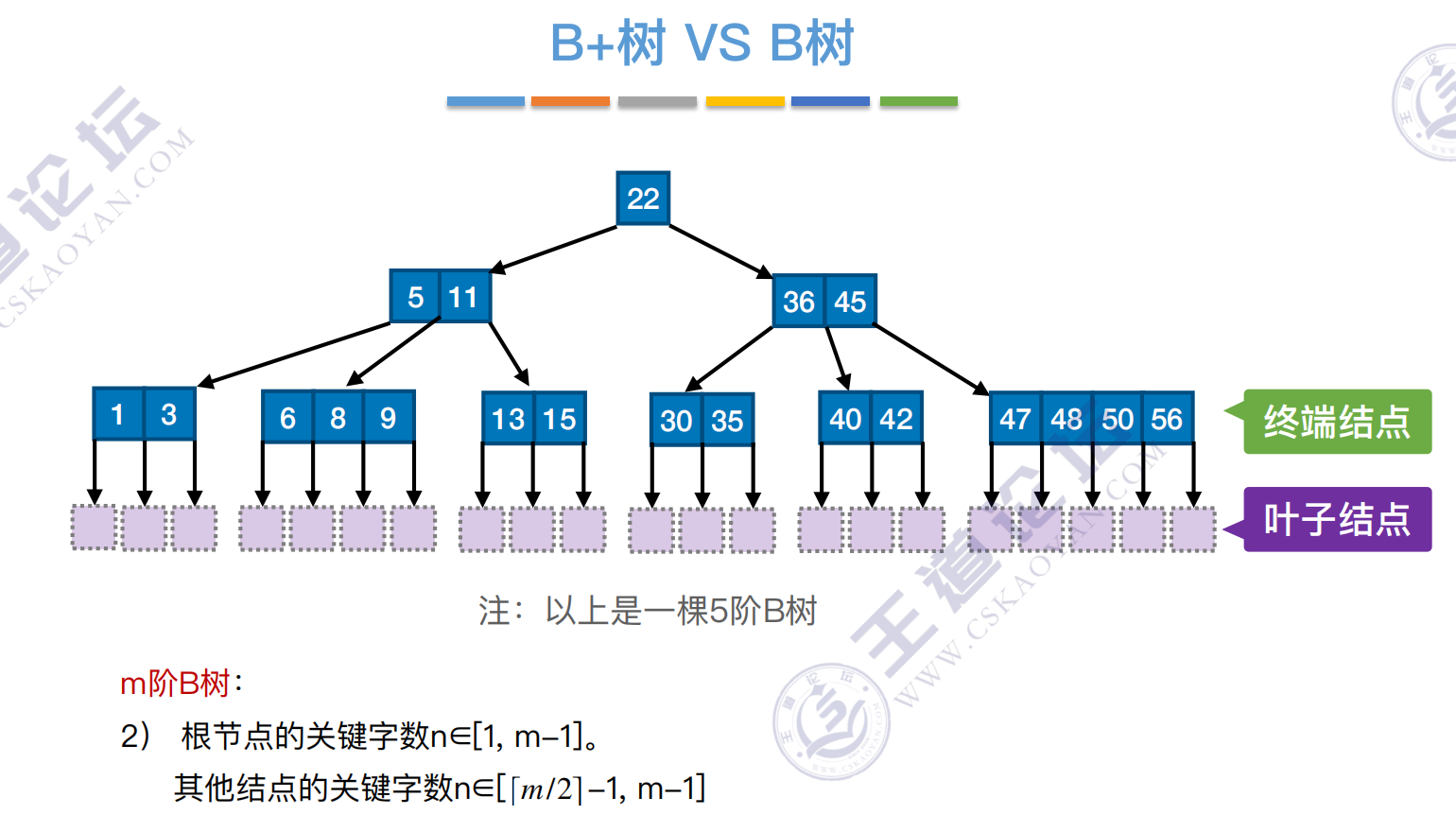
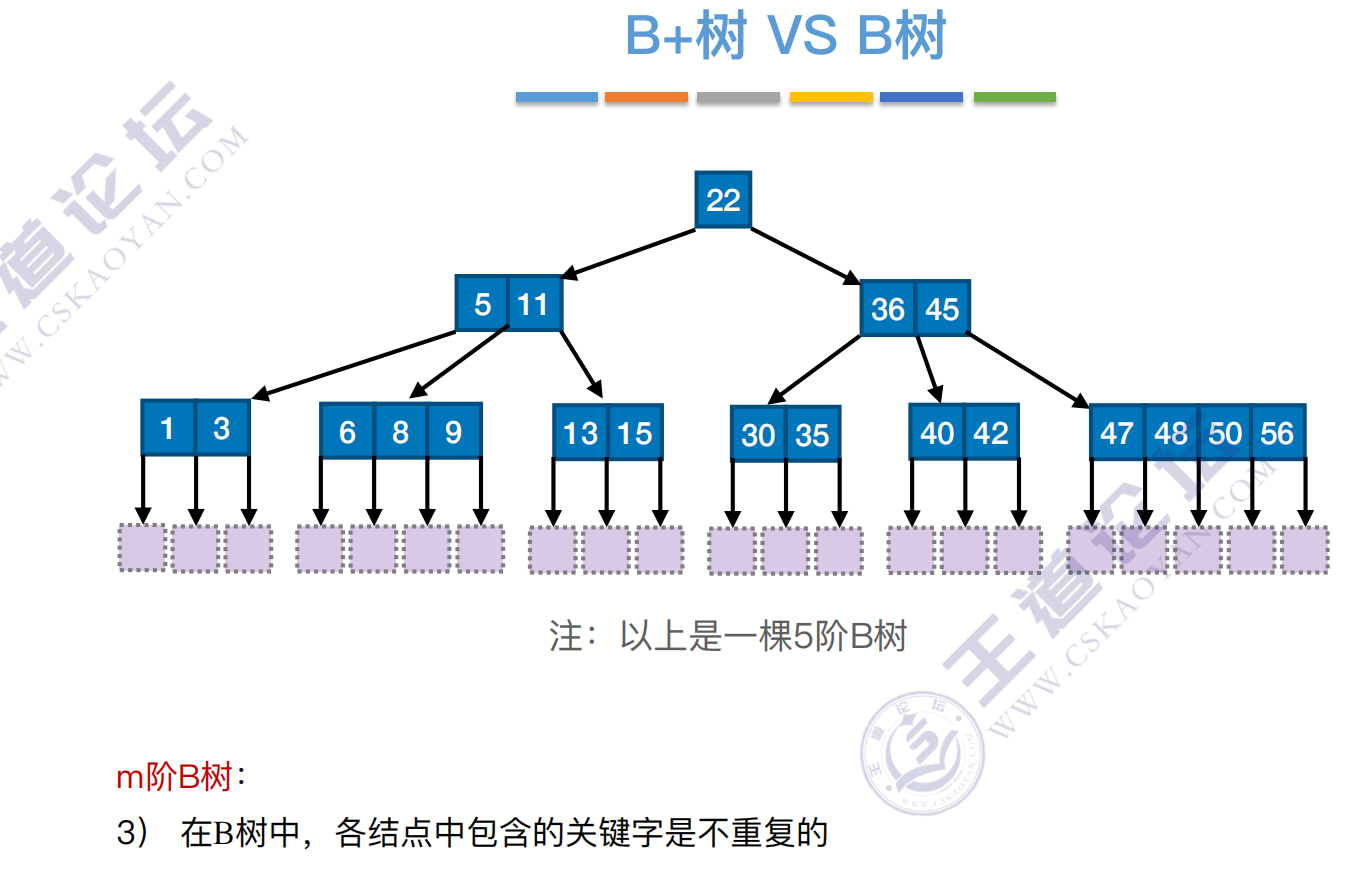
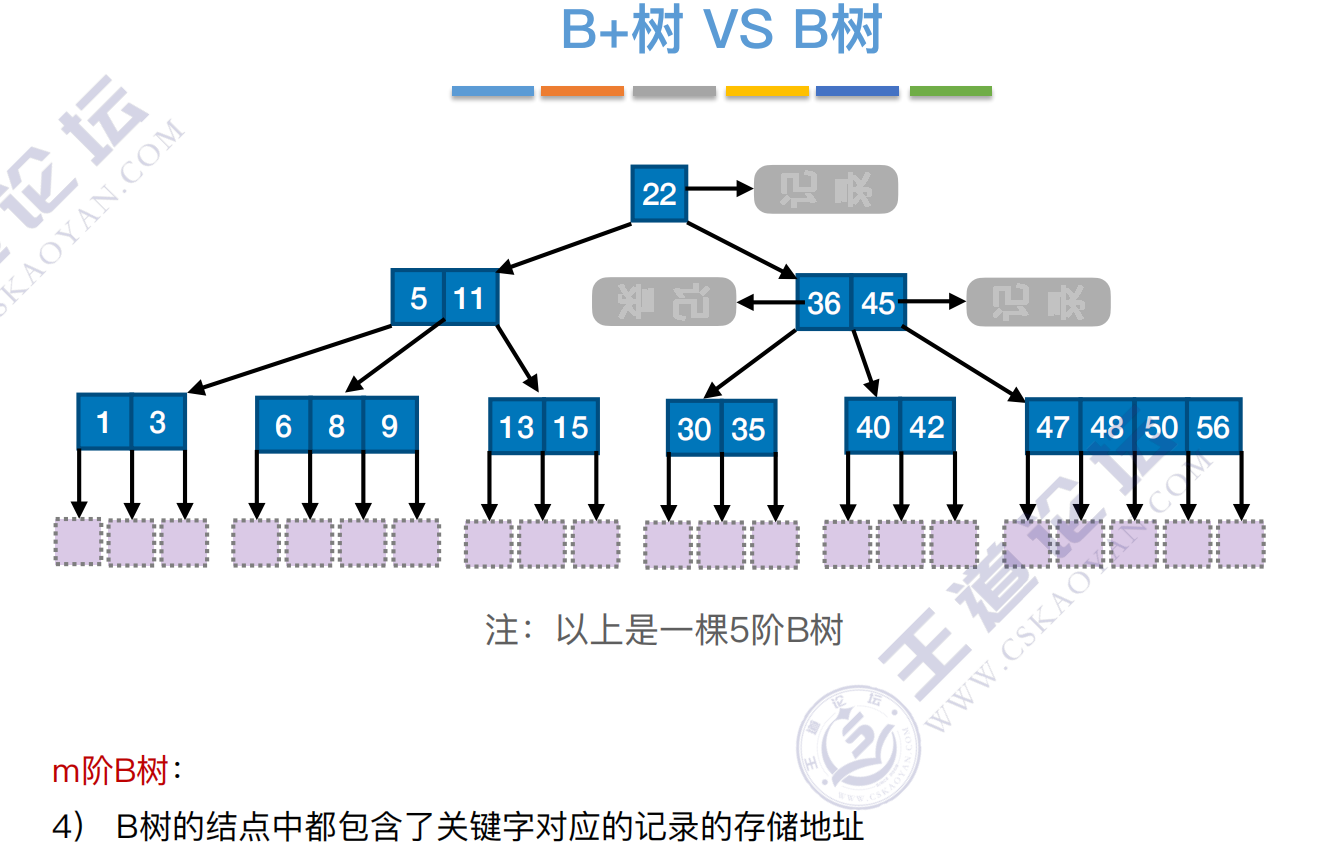
B树
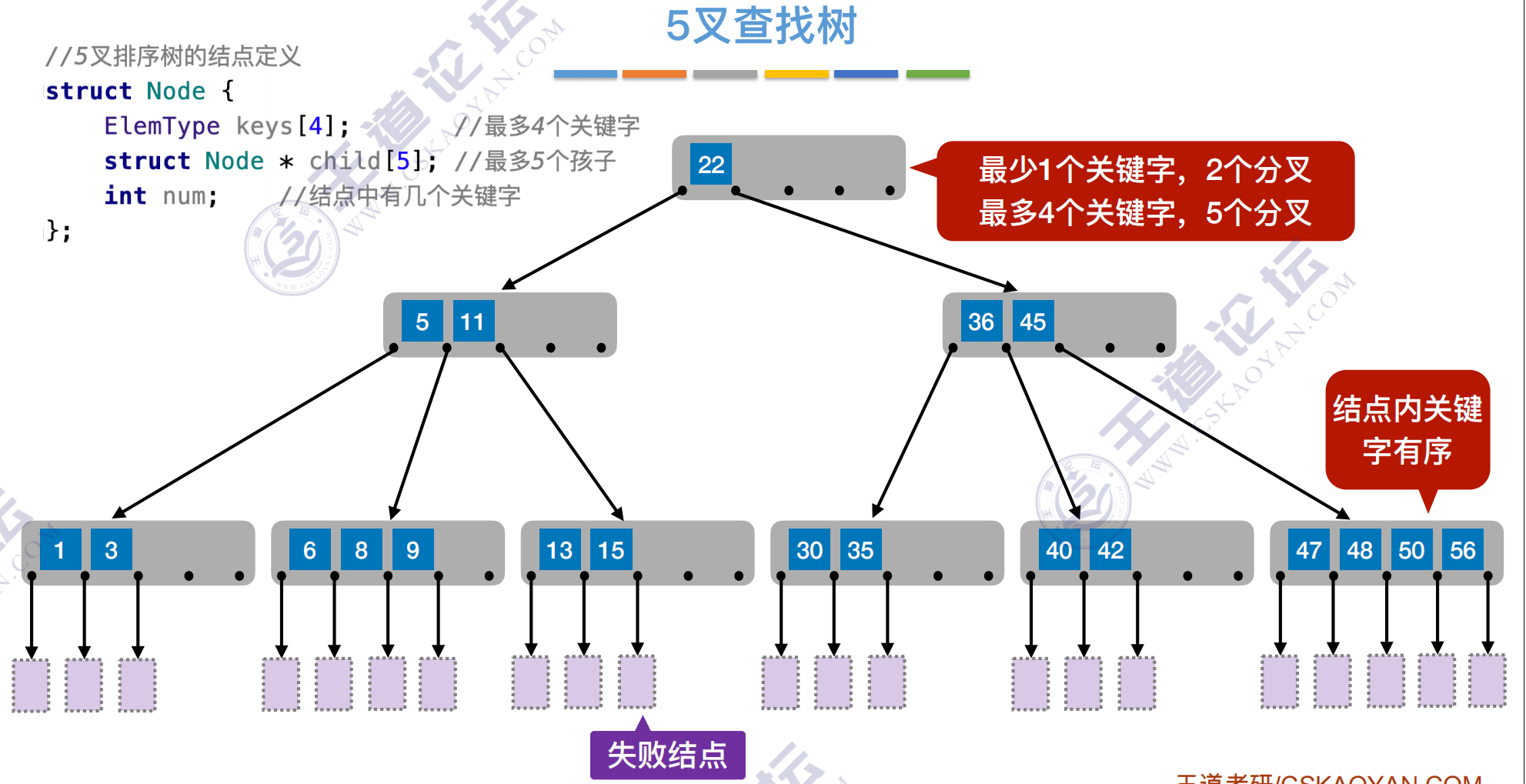
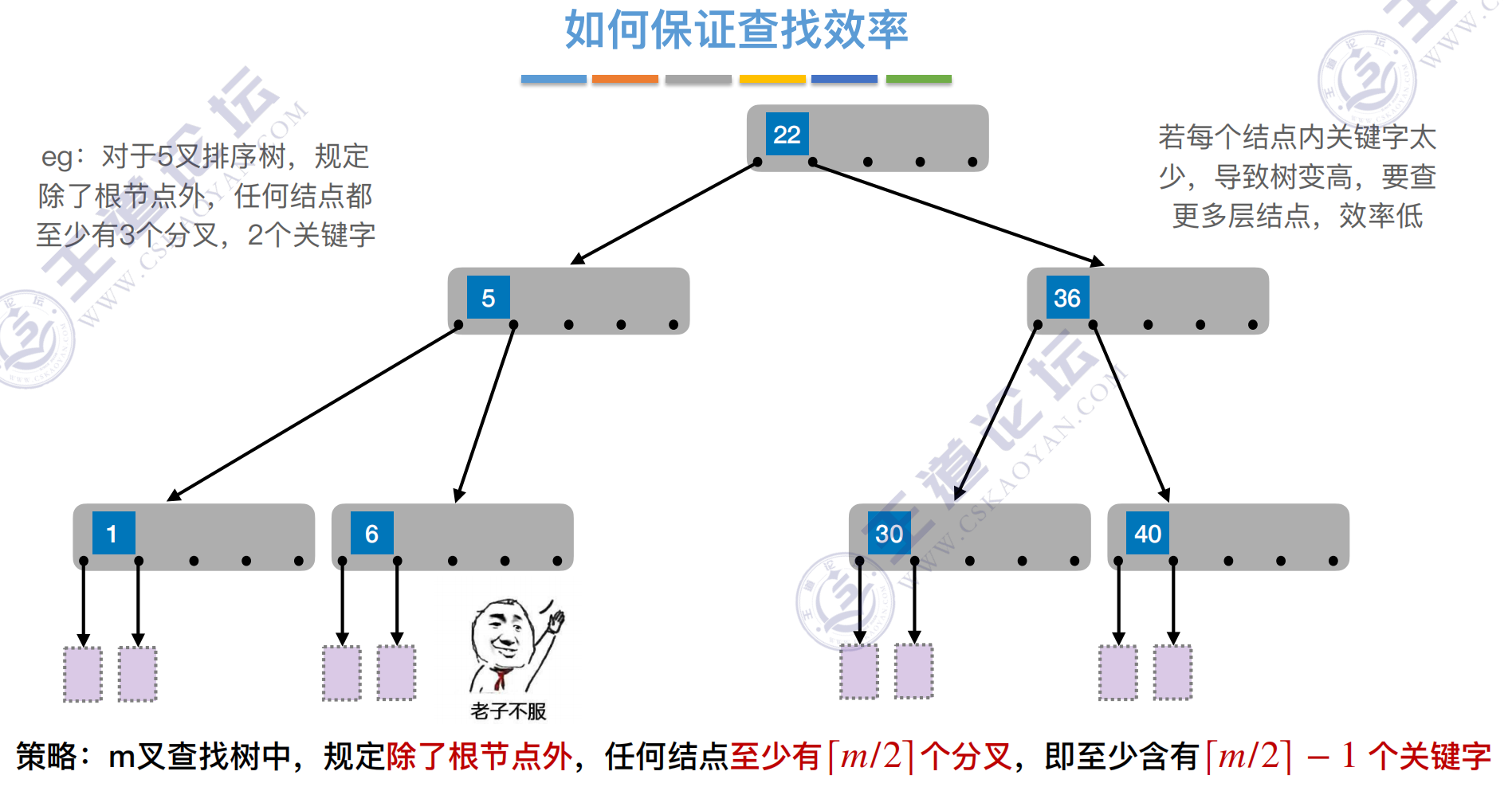
m叉查找树
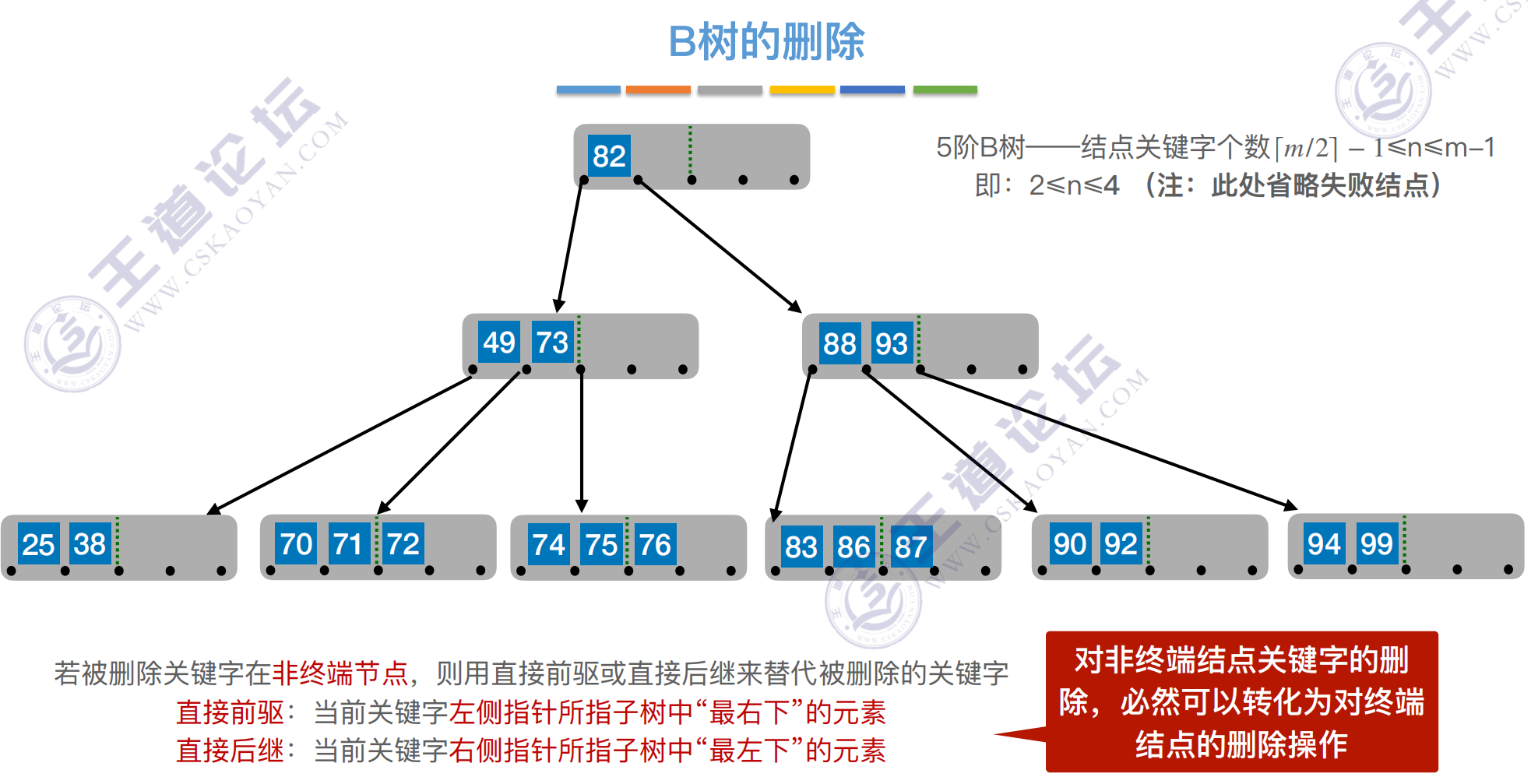
B树,⼜称多路平衡查找树,B树中所有结点的孩⼦个数的最⼤值称为B树的阶,通常⽤m表示。⼀棵m阶B树或为空树,或为满⾜如下特性的m叉树:
1)树中每个结点⾄多有m棵⼦树,即⾄多含有m-1个关键字。
2)若根结点不是终端结点,则⾄少有两棵⼦树。
3)除根结点外的所有⾮叶结点⾄少有 棵⼦树,即⾄少含有 -1个关键字。
4)所有的叶结点都出现在同⼀层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)。
性质
- 策略:m叉查找树中,规定对于任何⼀个结点,其所有⼦树的⾼度都要相同。
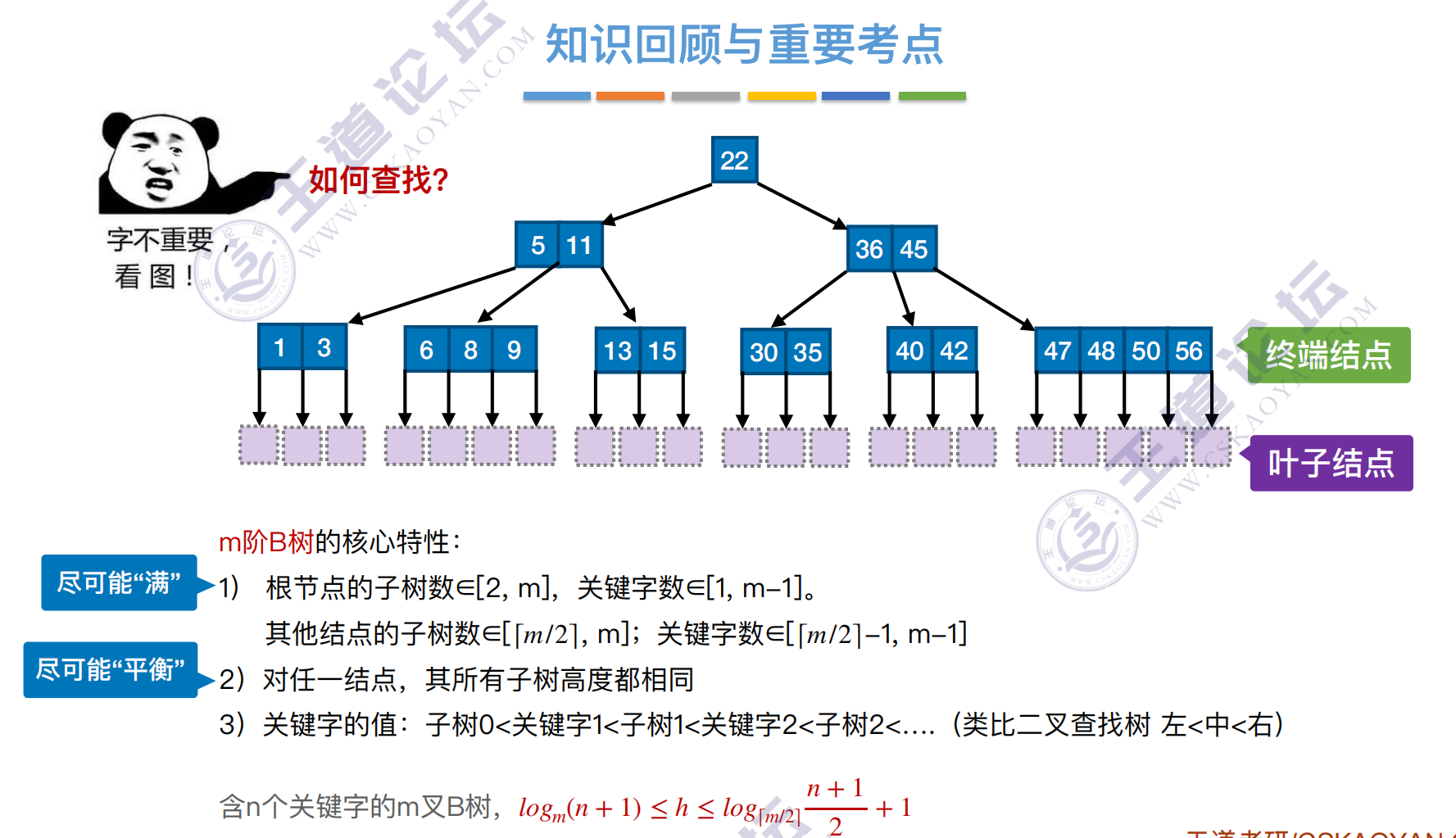
m阶B树的核⼼特性:
1) 根节点的⼦树数∈[2, m],关键字数∈[1, m-1]。
其他结点的⼦树数∈[ , m];关键字数∈[ -1, m-1]
2)对任⼀结点,其所有⼦树⾼度都相同
3)关键字的值:⼦树0<关键字1<⼦树1<关键字2<⼦树2<…. (类⽐⼆叉查找树 左<中<右)
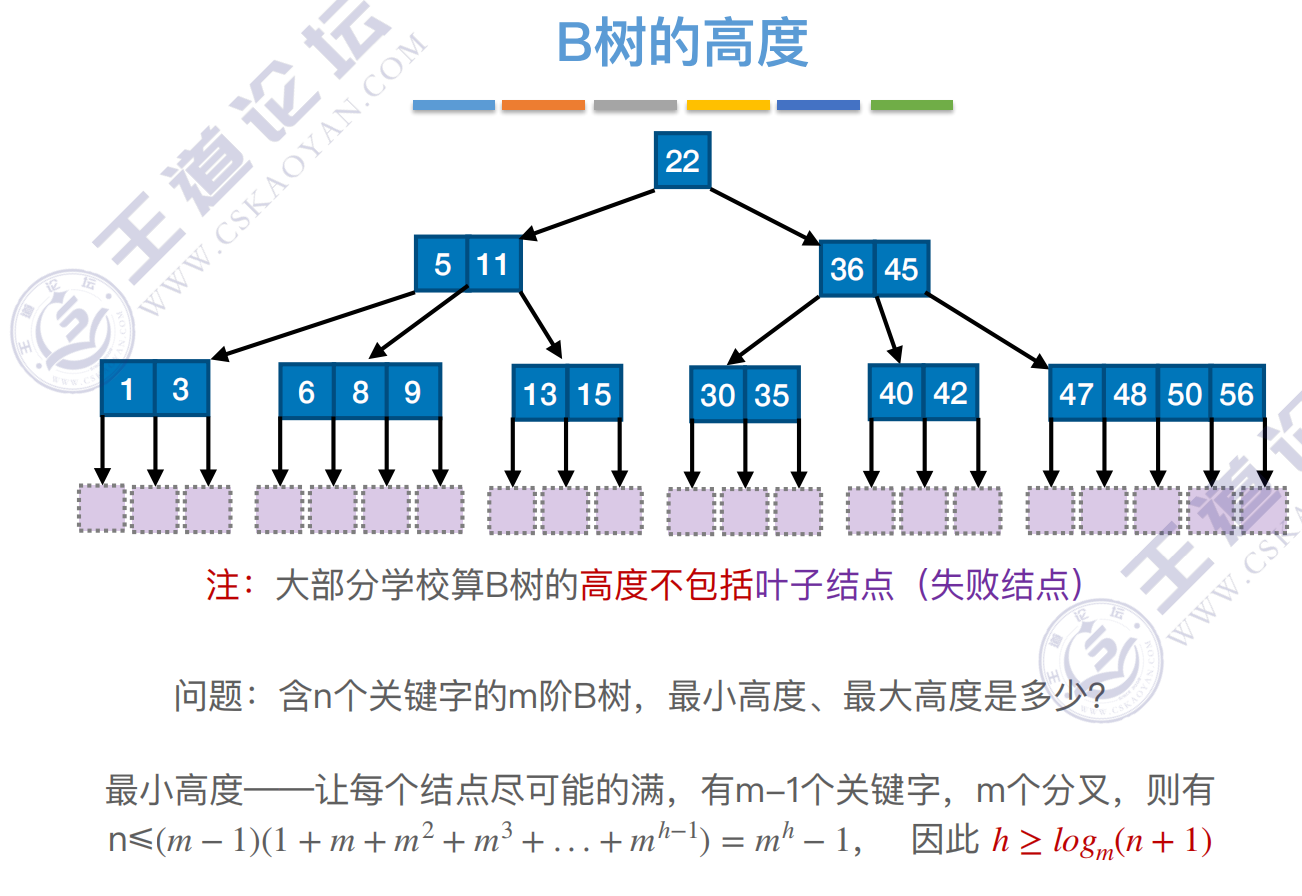
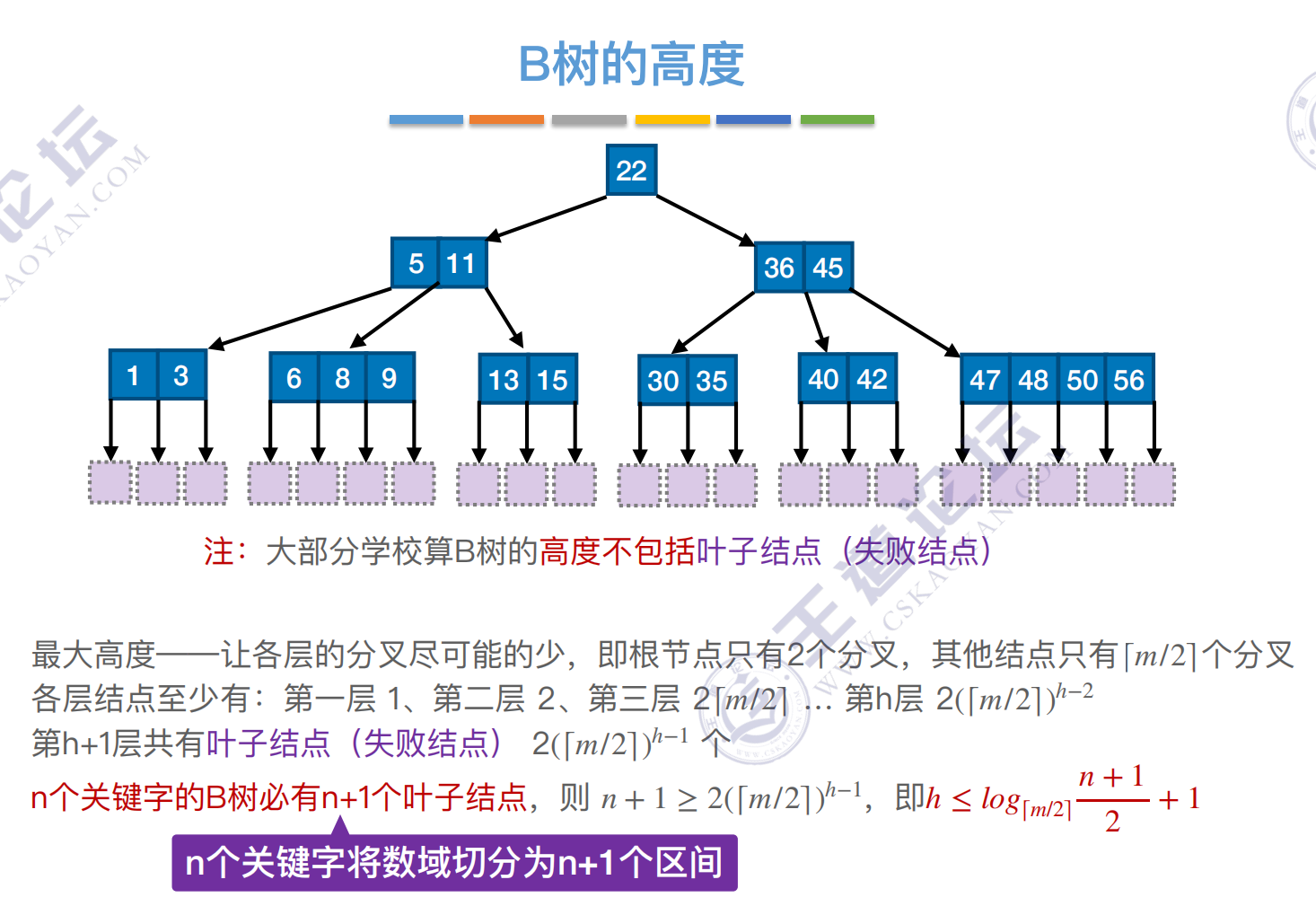
b树的高度
总结
B树的插入和删除
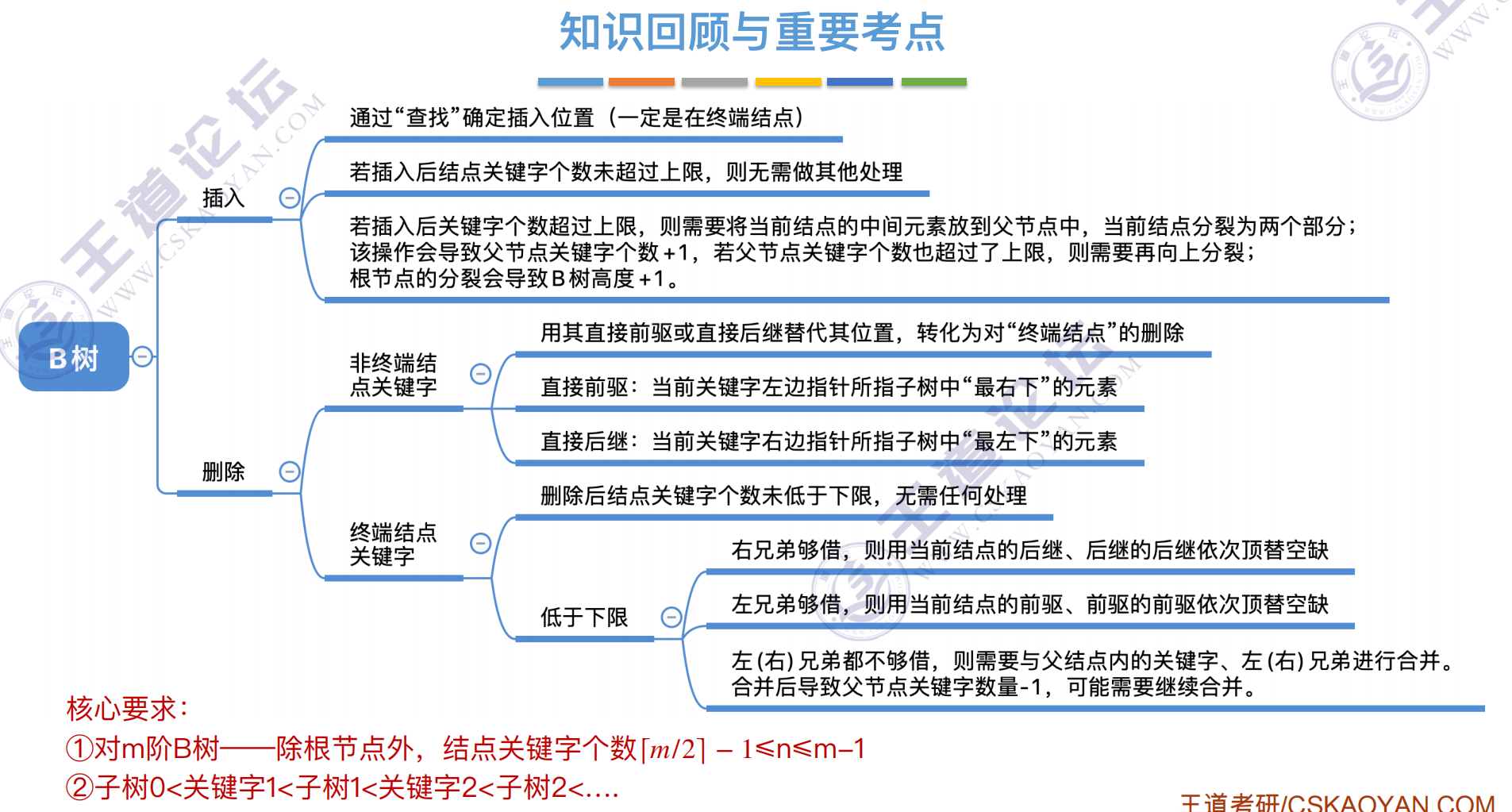
插入
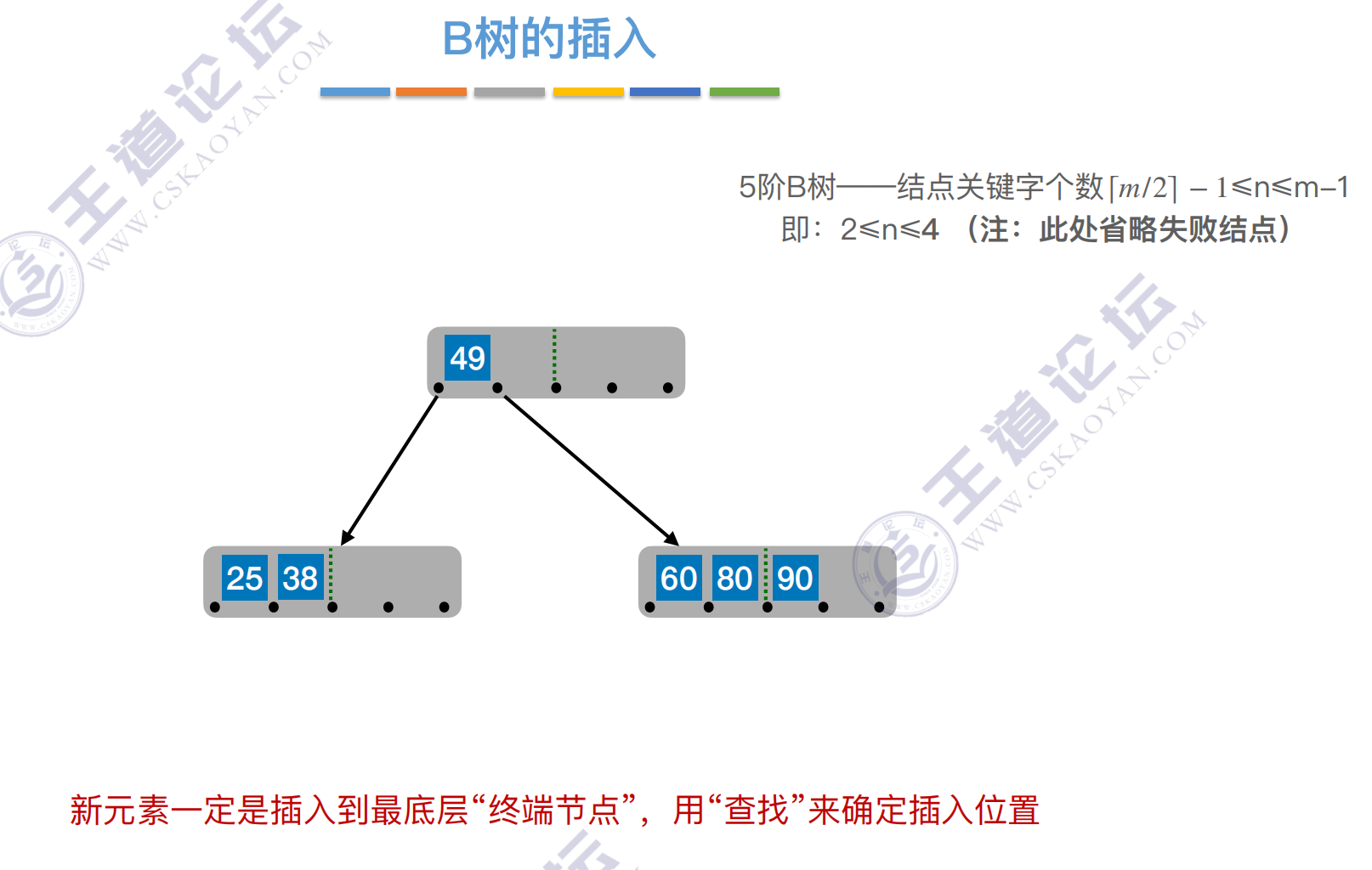
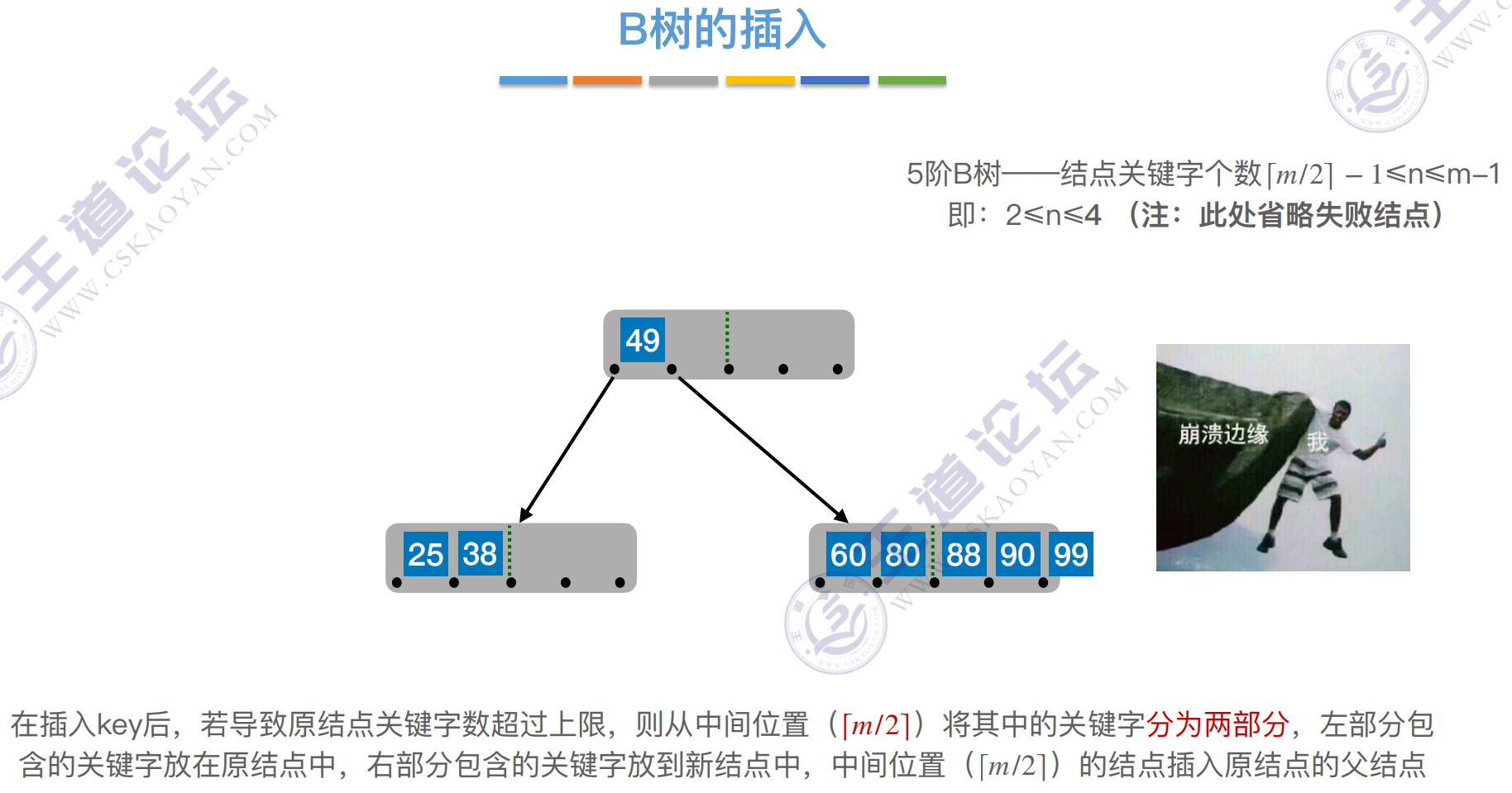
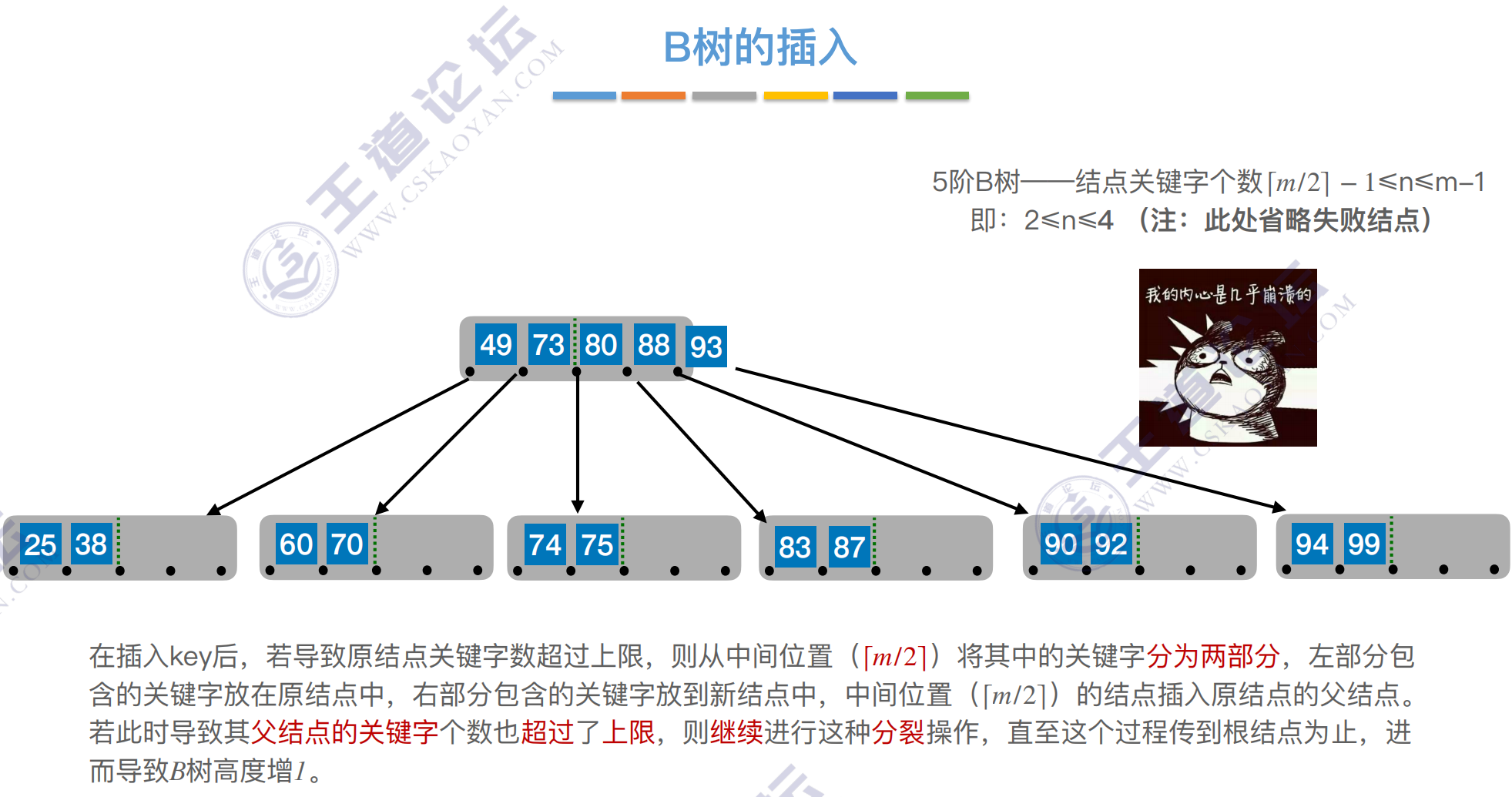
核⼼要求:
①对m阶B树——除根节点外,结点关键字个数 ≤n≤m-1
②⼦树0<关键字1<⼦树1<关键字2<⼦树2<…. ⌈m/2⌉ − 1
新元素⼀定是插⼊到最底层“终端节点”,⽤“查找”来确定插⼊位置
在插⼊key后,若导致原结点关键字数超过上限,则从中间位置(⌈m/2⌉)将其中的关键字分为两部分,左部分包
含的关键字放在原结点中,右部分包含的关键字放到新结点中,中间位置(⌈m/2⌉)的结点插⼊原结点的⽗结点。
若此时导致其⽗结点的关键字个数也超过了上限,则继续进⾏这种分裂操作,直⾄这个过程传到根结点为⽌,进
⽽导致B树⾼度增1。
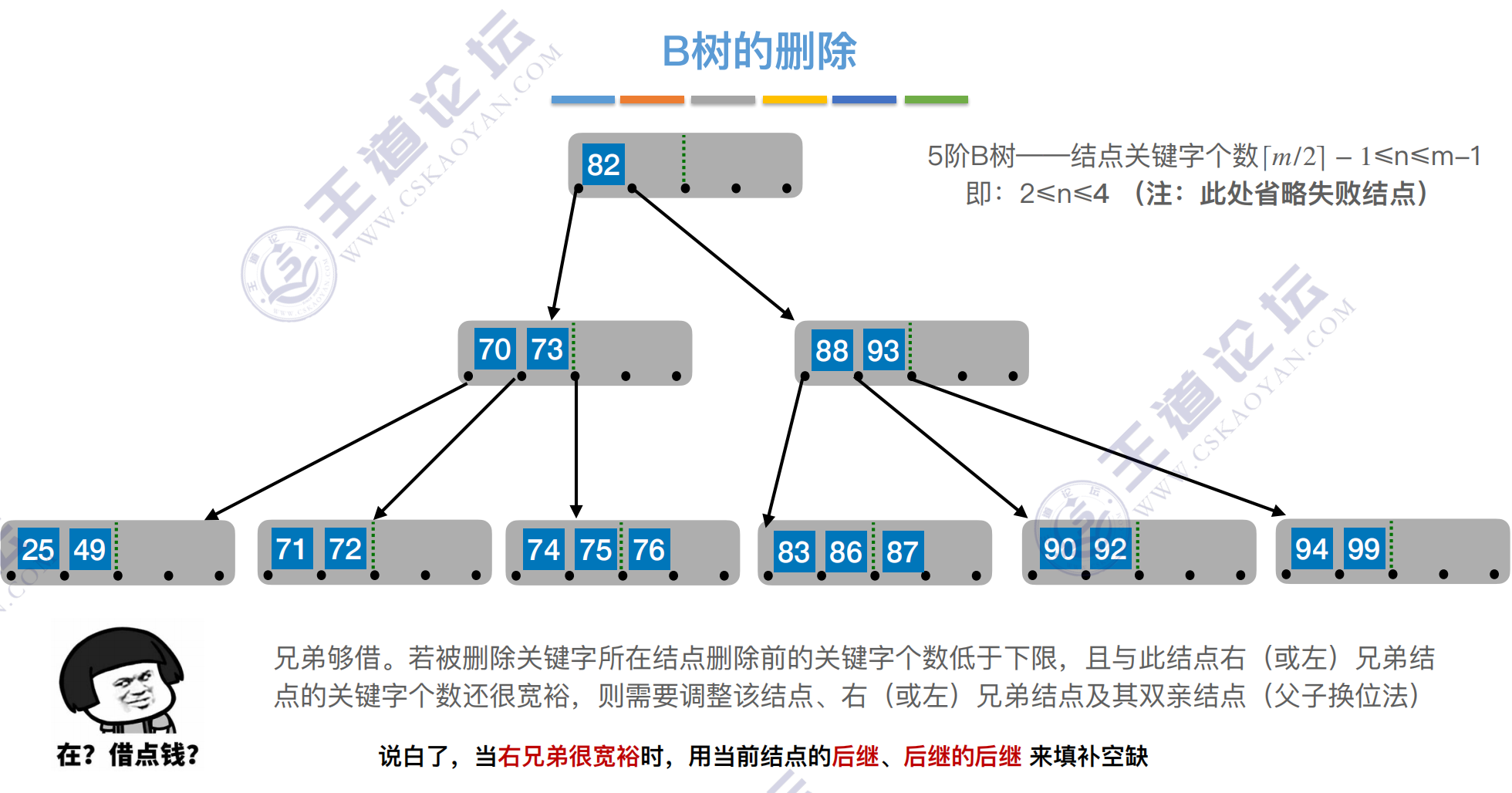
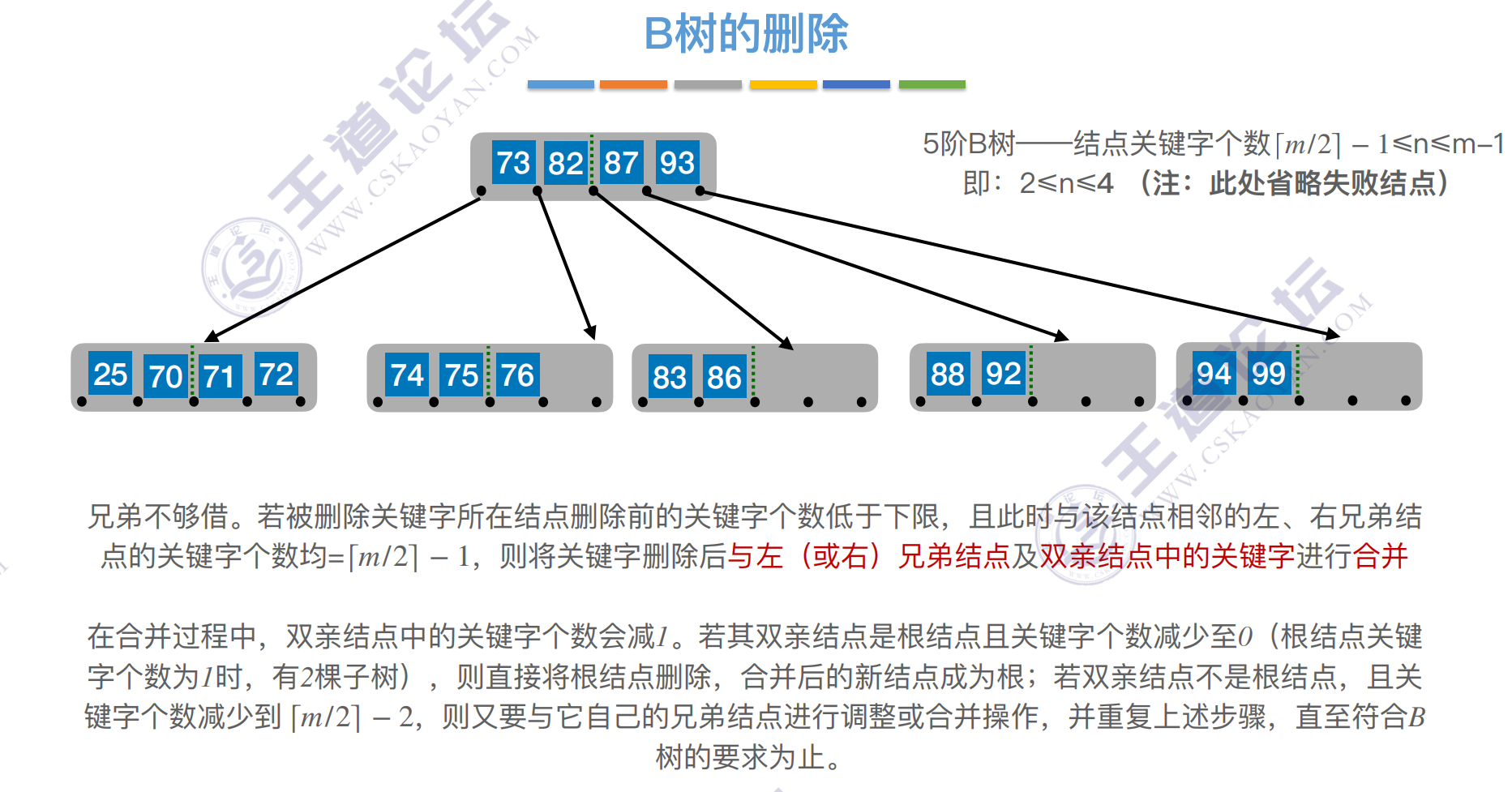
删除
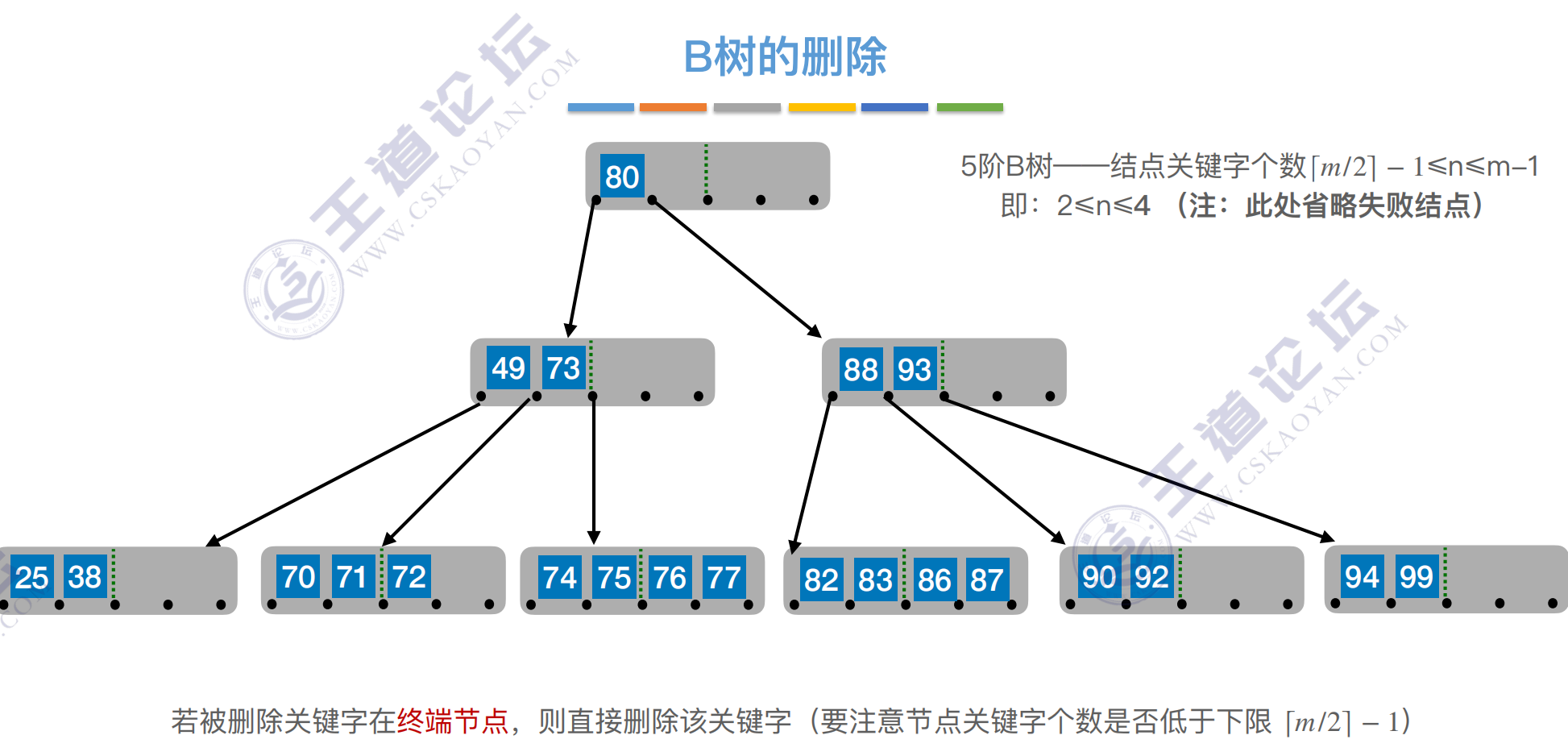
总结
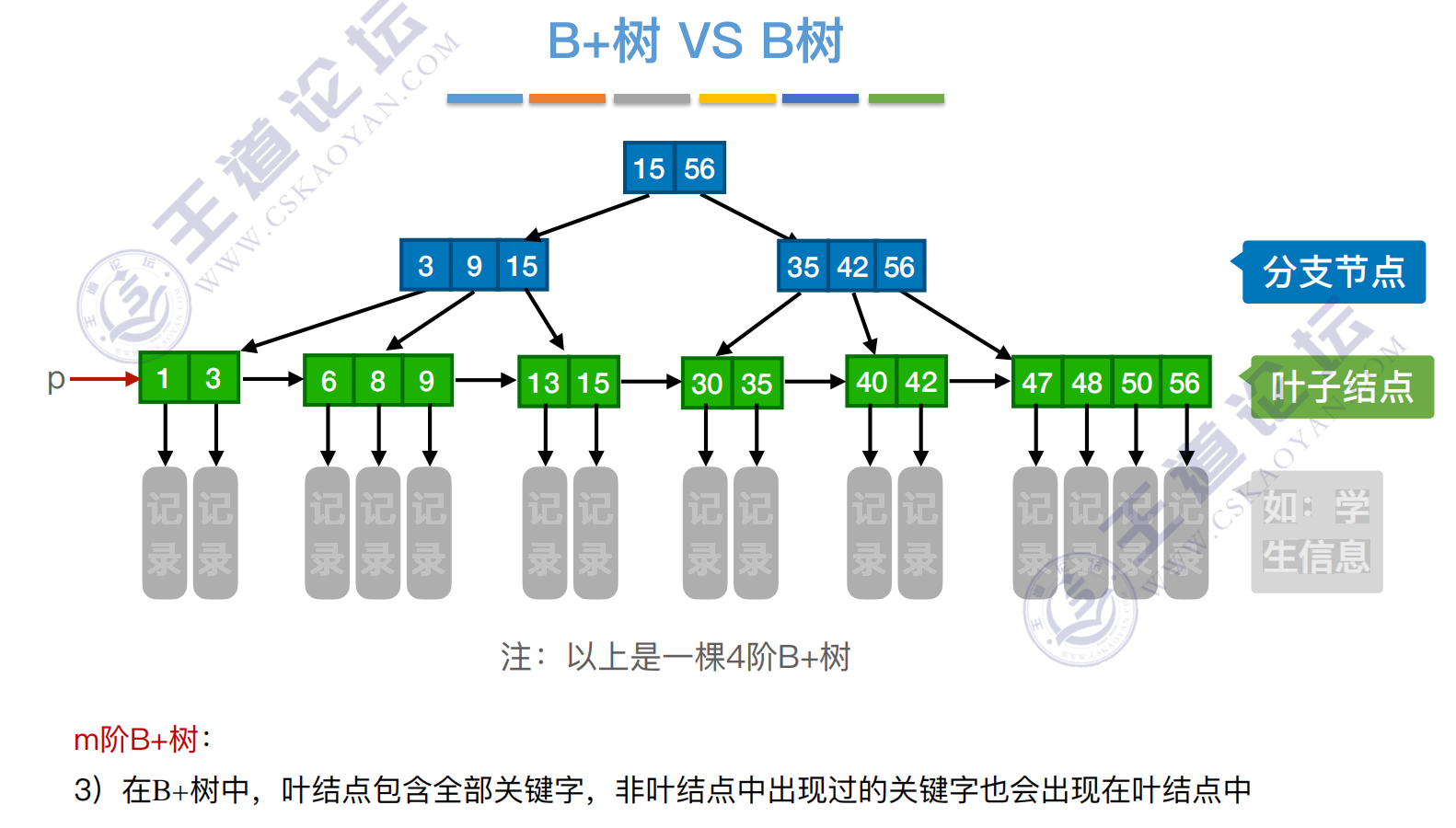
B+树
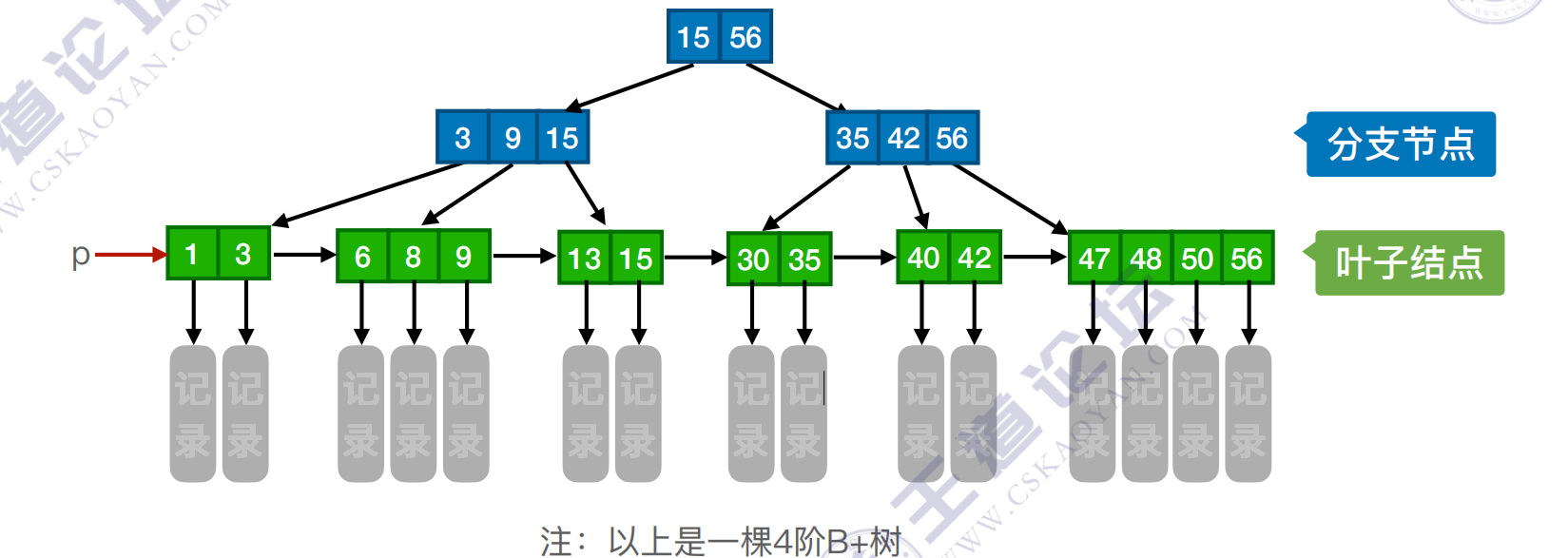
一棵m阶的B+树需满⾜下列条件:
1)每个分⽀结点最多有m棵⼦树(孩⼦结点)。
2)⾮叶根结点⾄少有两棵⼦树,其他每个分⽀结点⾄少有⌈m/2⌉棵⼦树。
3)结点的⼦树个数与关键字个数相等。
4)所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按⼤⼩顺序排列,并且相邻叶结点按⼤⼩顺序相互链接起来。
5)所有分⽀结点中仅包含它的各个⼦结点中关键字的最⼤值及指向其⼦结点的指针。
B+树中,⽆论查找成功与否,最终⼀定都要⾛到最下⾯⼀层结点
B+树与B树对比
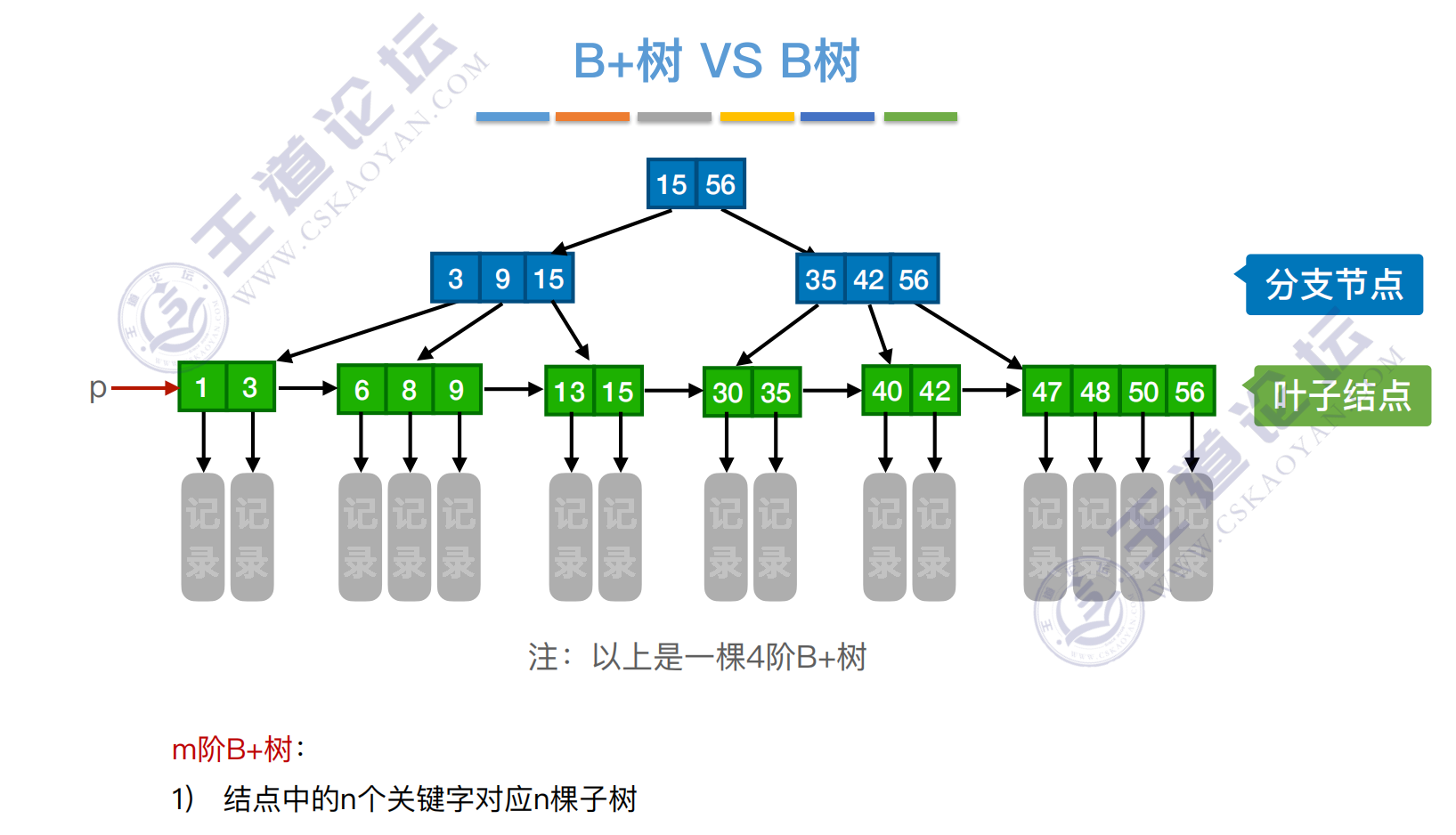
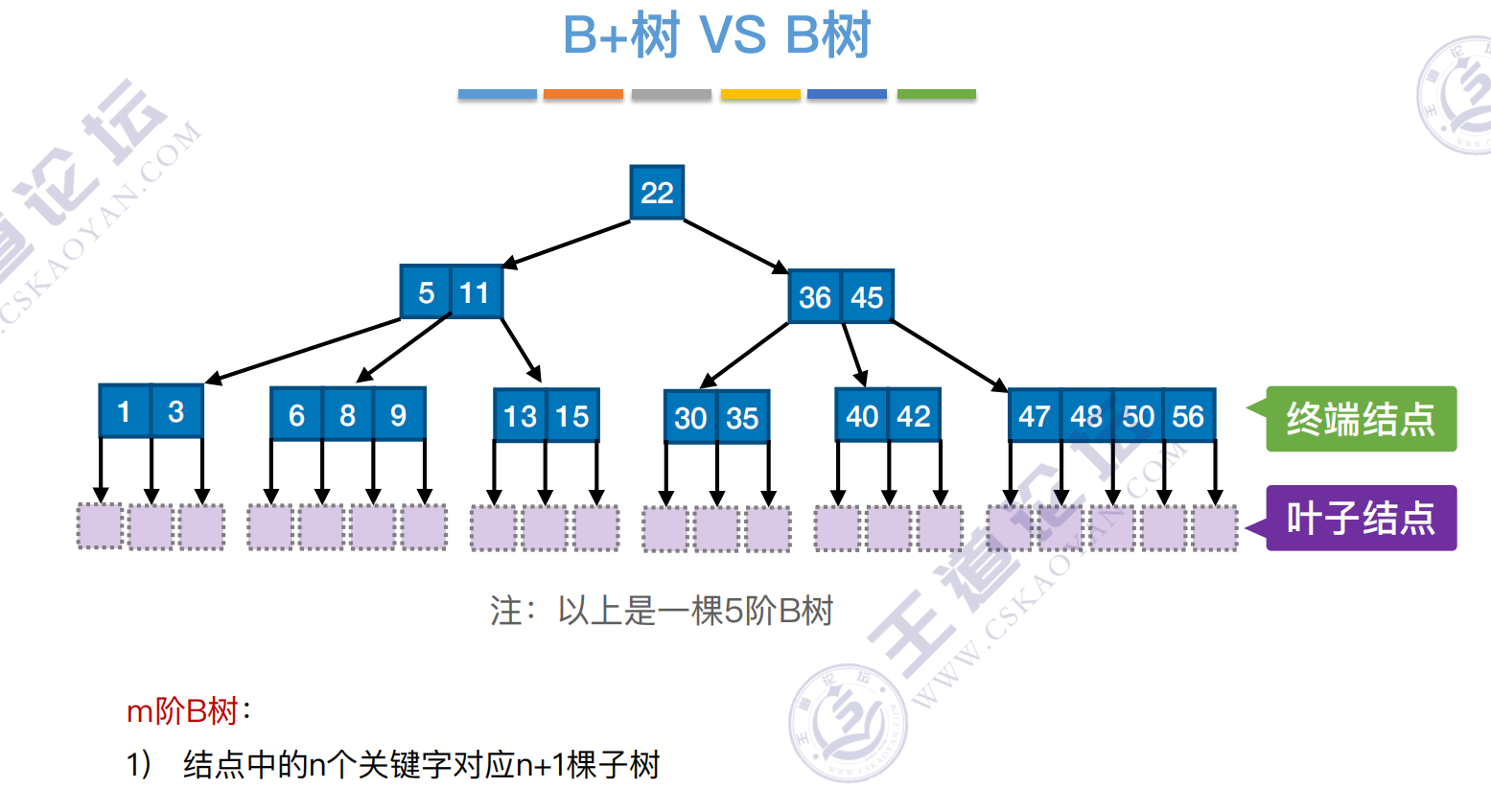
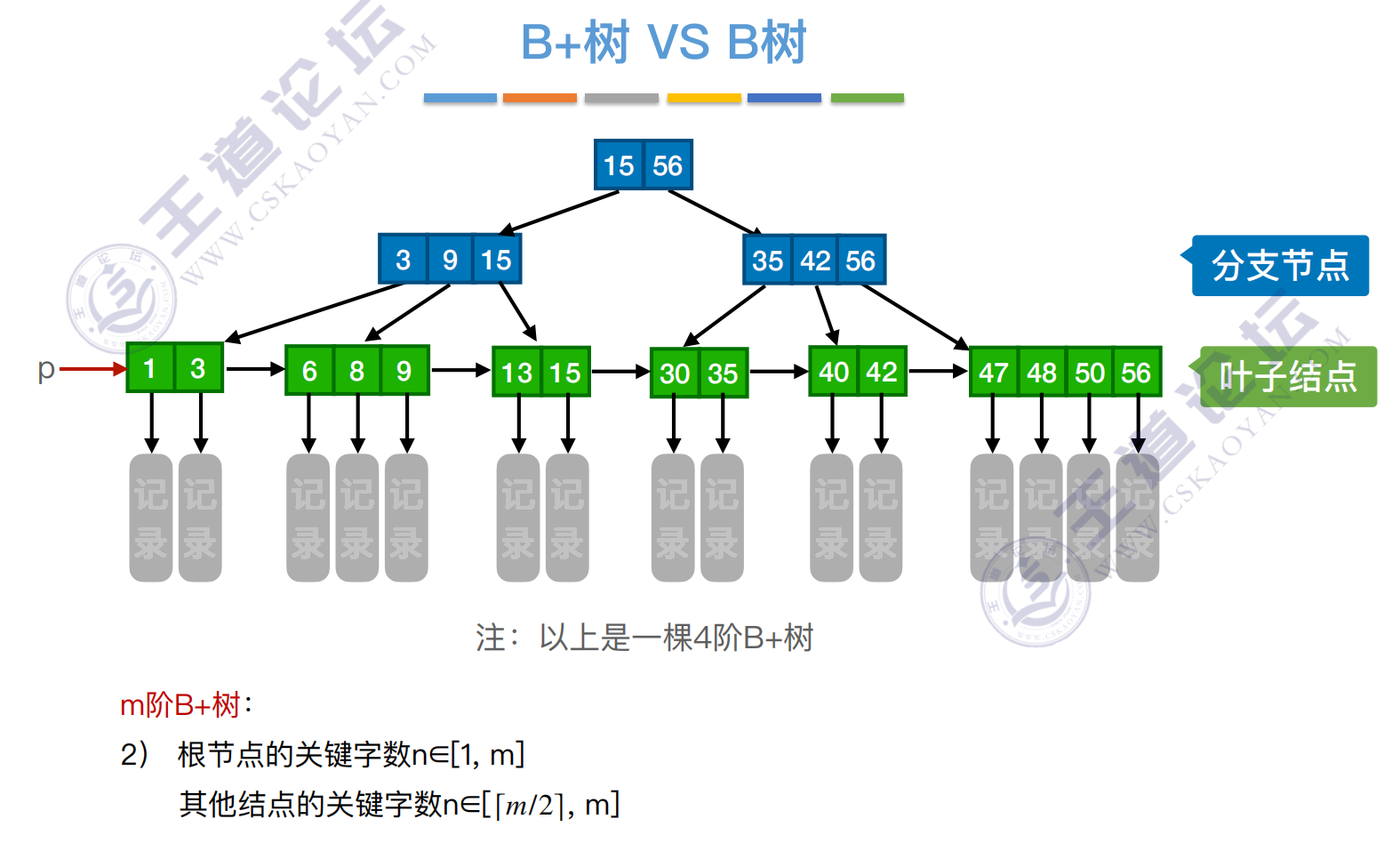
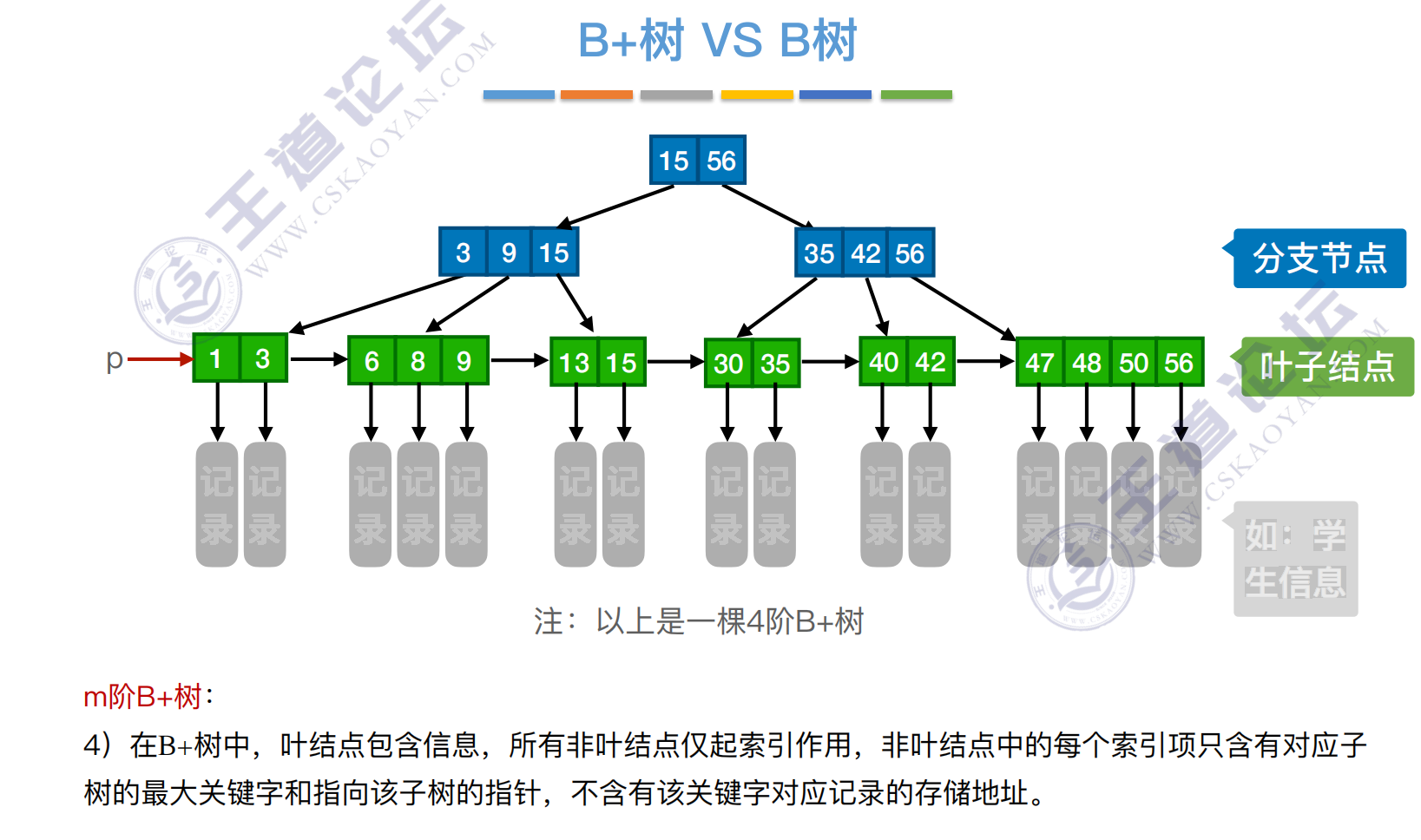
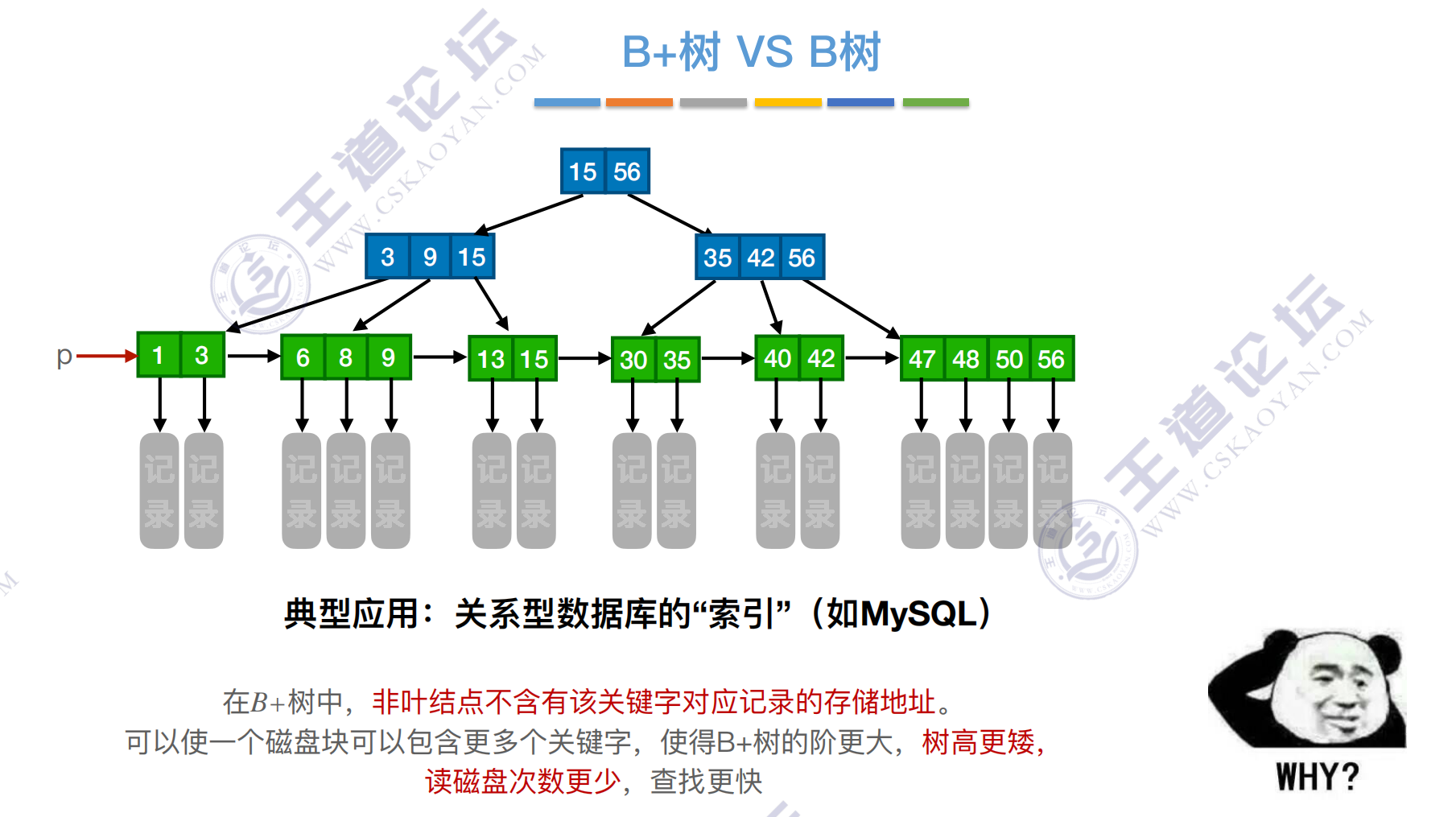
在B+树中,⾮叶结点不含有该关键字对应记录的存储地址。
可以使⼀个磁盘块可以包含更多个关键字,使得B+树的阶更⼤,树⾼更矮,
读磁盘次数更少,查找更快
总结

散列查找(哈希)
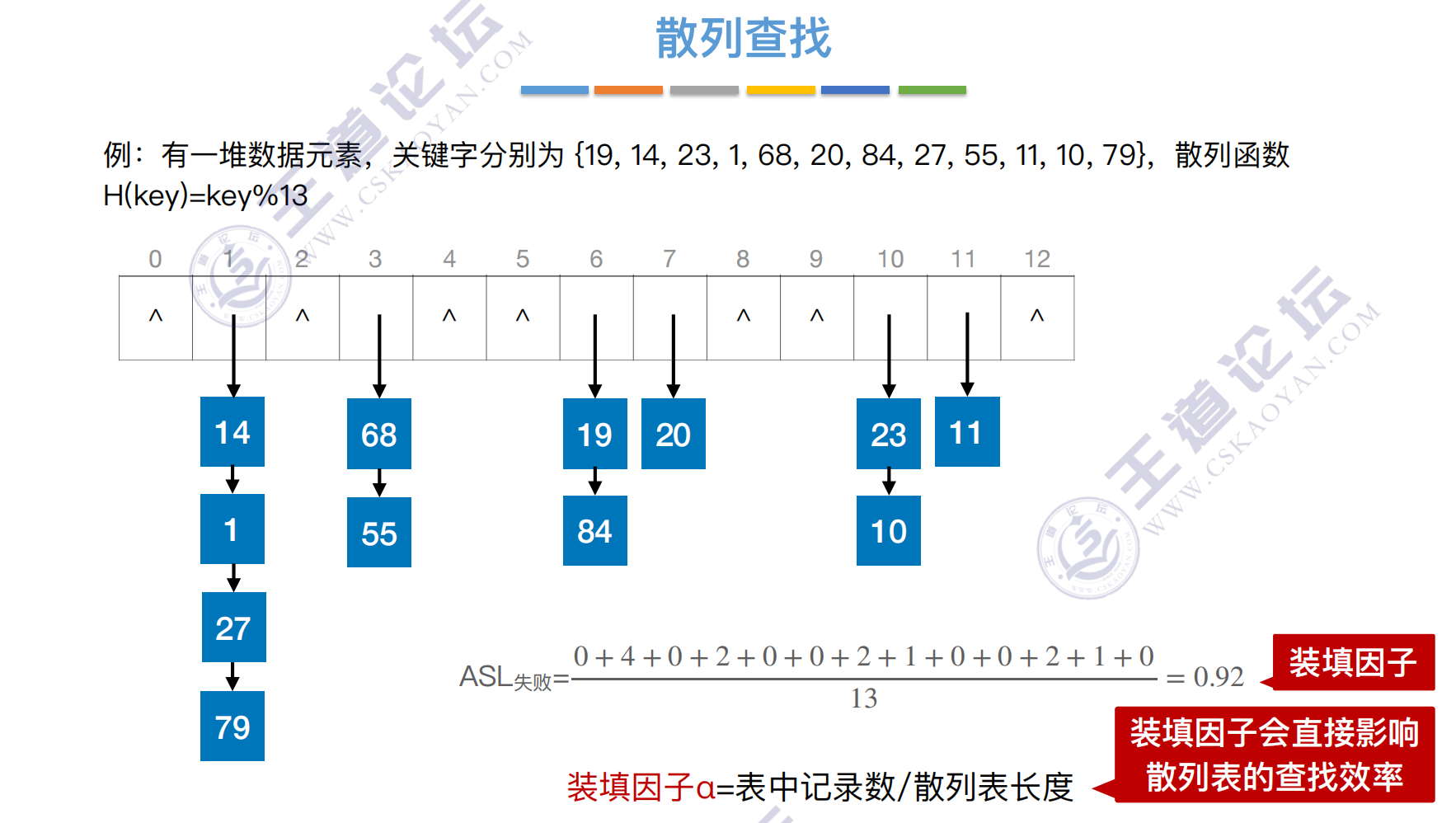
散列表(Hash Table),⼜称哈希表。是⼀种数据结构,特点是:数据元素的关键字与其存储地址直接相关
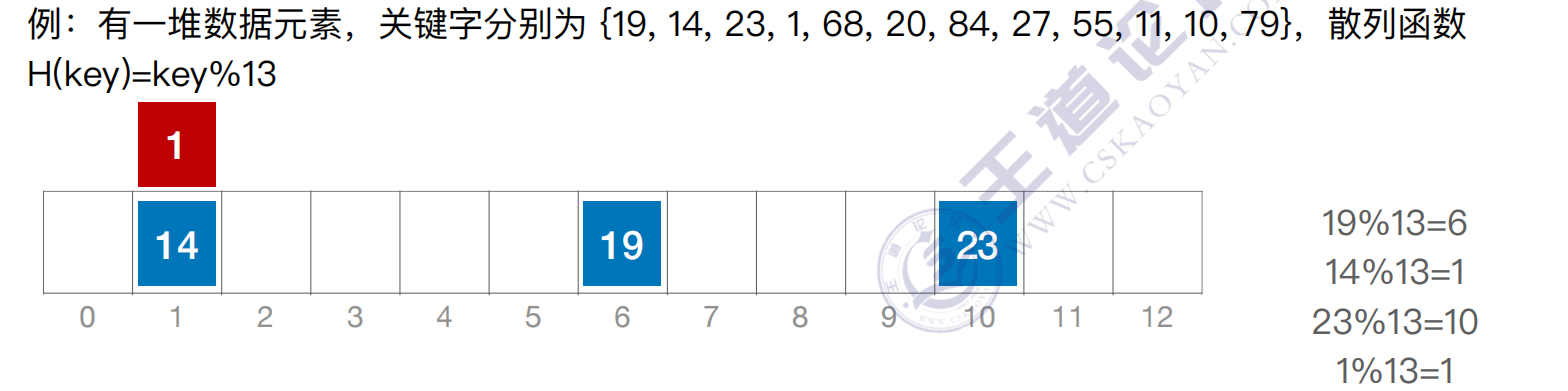
若不同的关键字通过散列函数映射到同⼀个值,则称它们为“同义词”
通过散列函数确定的位置已经存放了其他元素,则称这种情况为“冲突”
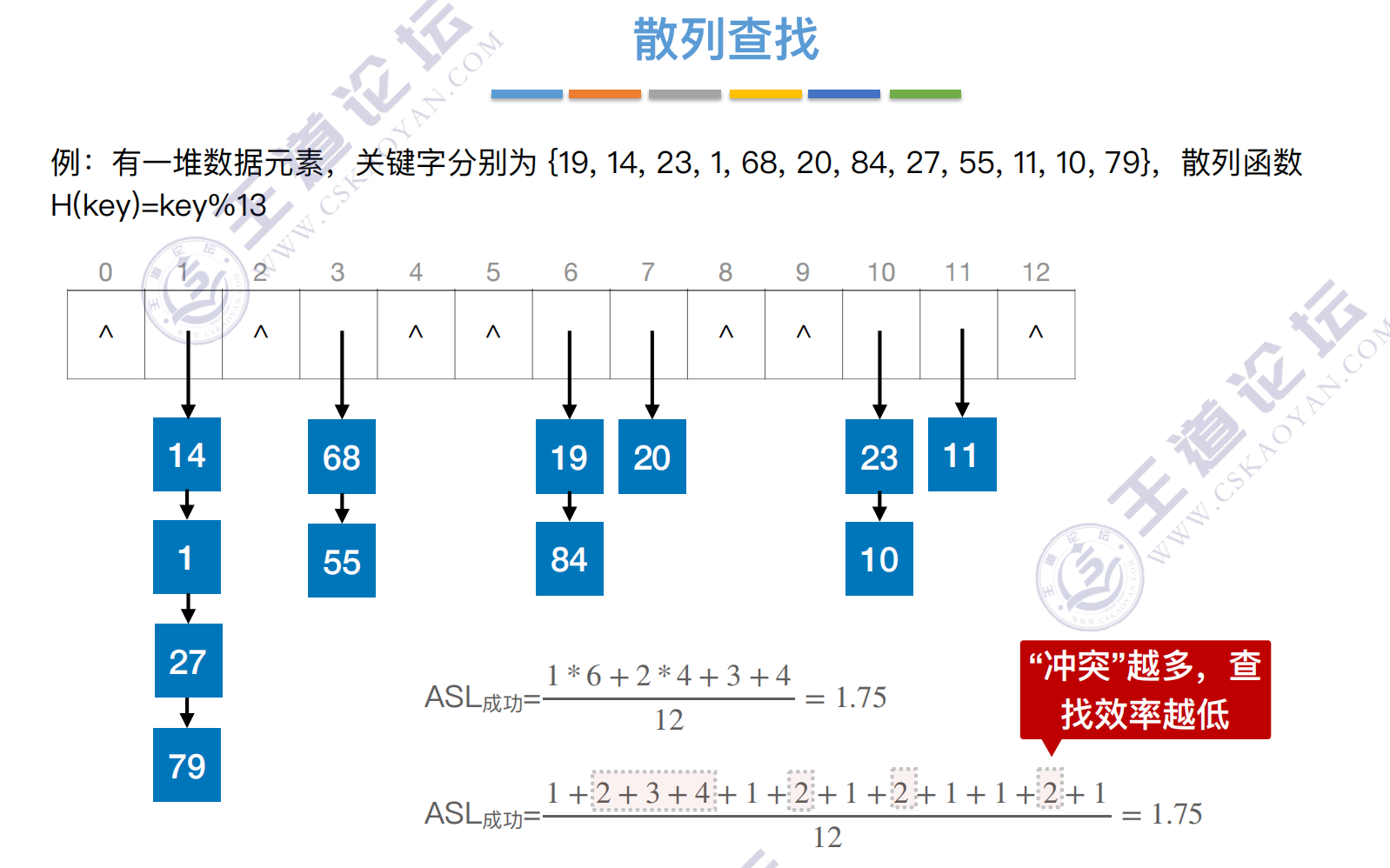
处理冲突:拉链法

处理冲突:开放定址法

线性探测法

删除操作

查找效率分析


线性探测法很容易造成同义词、⾮同义词的“聚集(堆积)”现象,严重影响查找效率
产⽣原因——冲突后再探测⼀定是放在某个连续的位置
平方探测法

⾮重点⼩坑:散列表⻓度m必须是⼀个可以表示成4j + 3的素数,才能探测到所有位置
处理冲突:再散列法

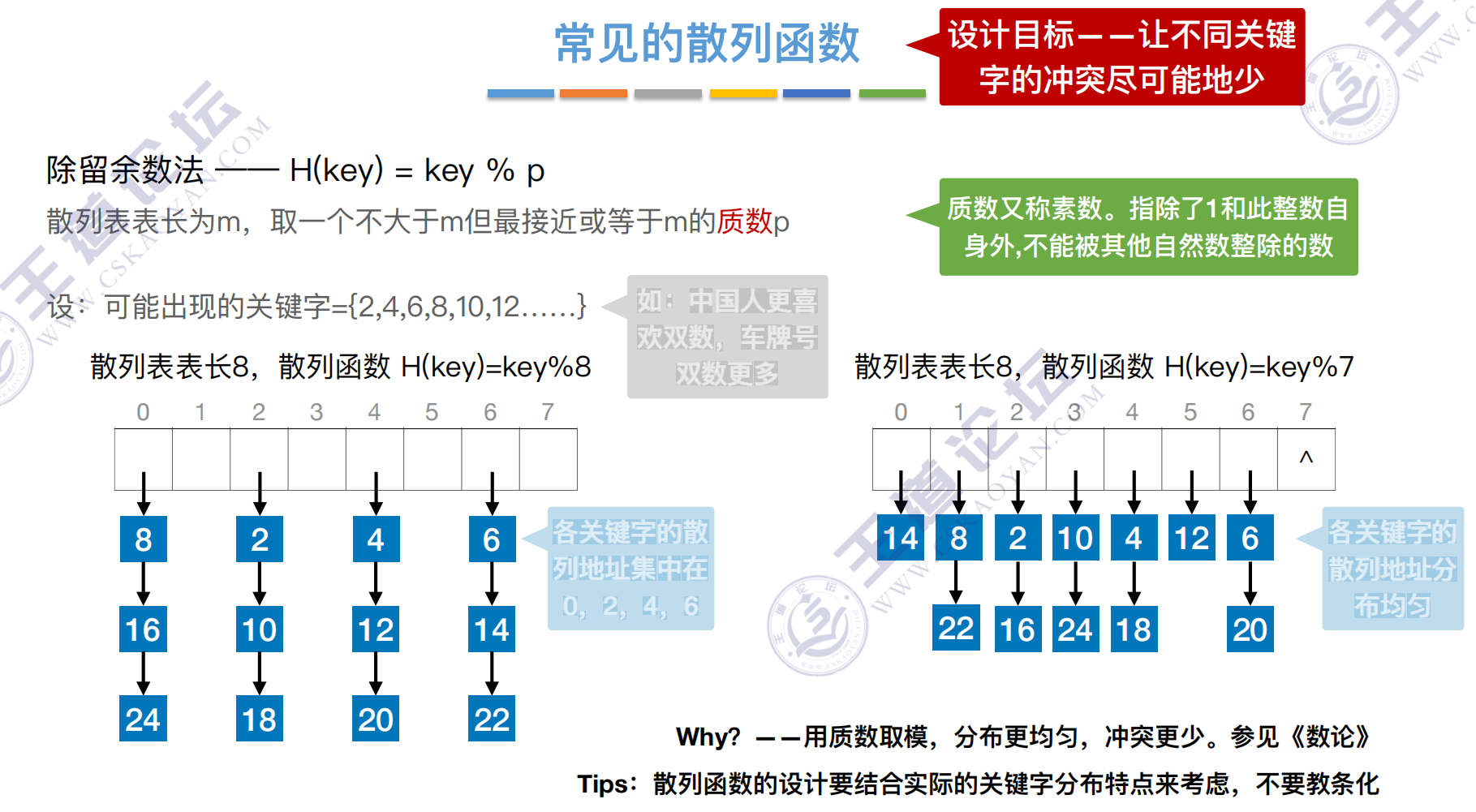
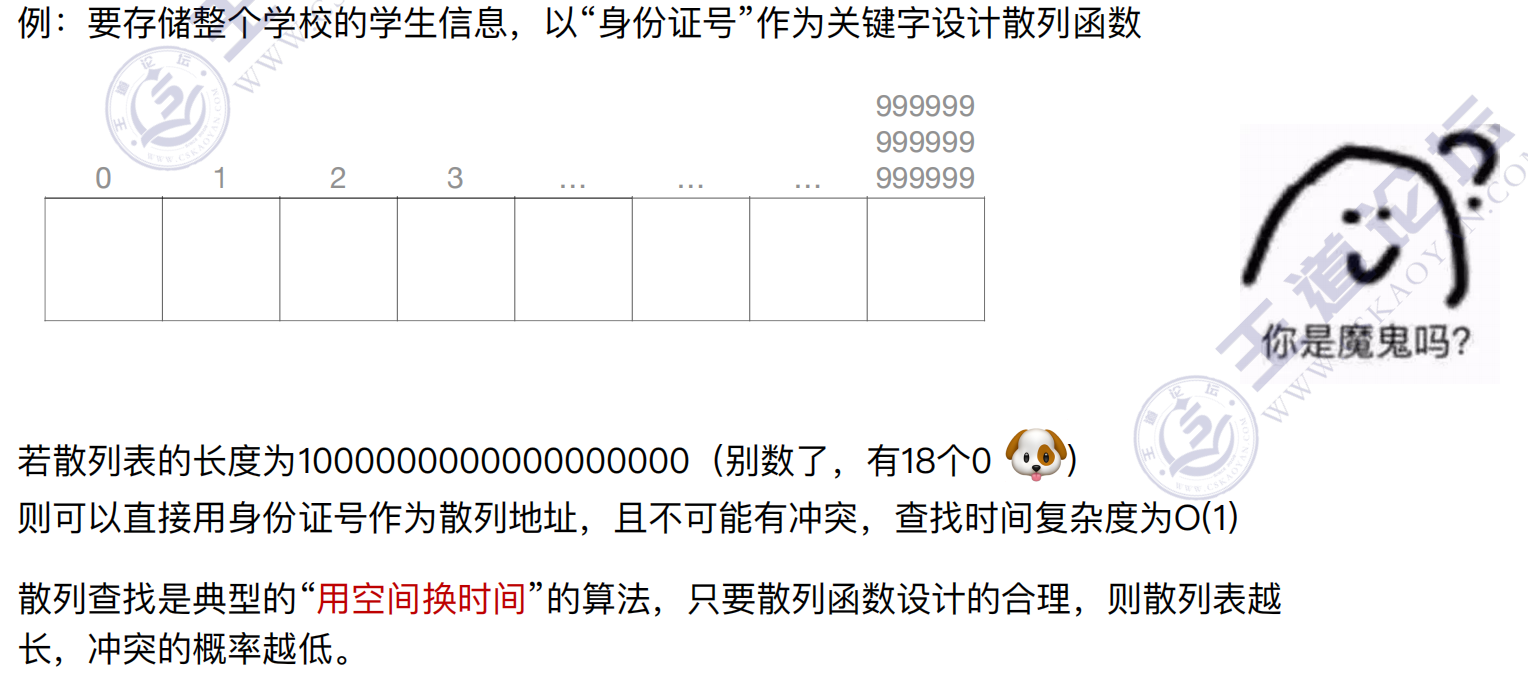
常见的散列函数



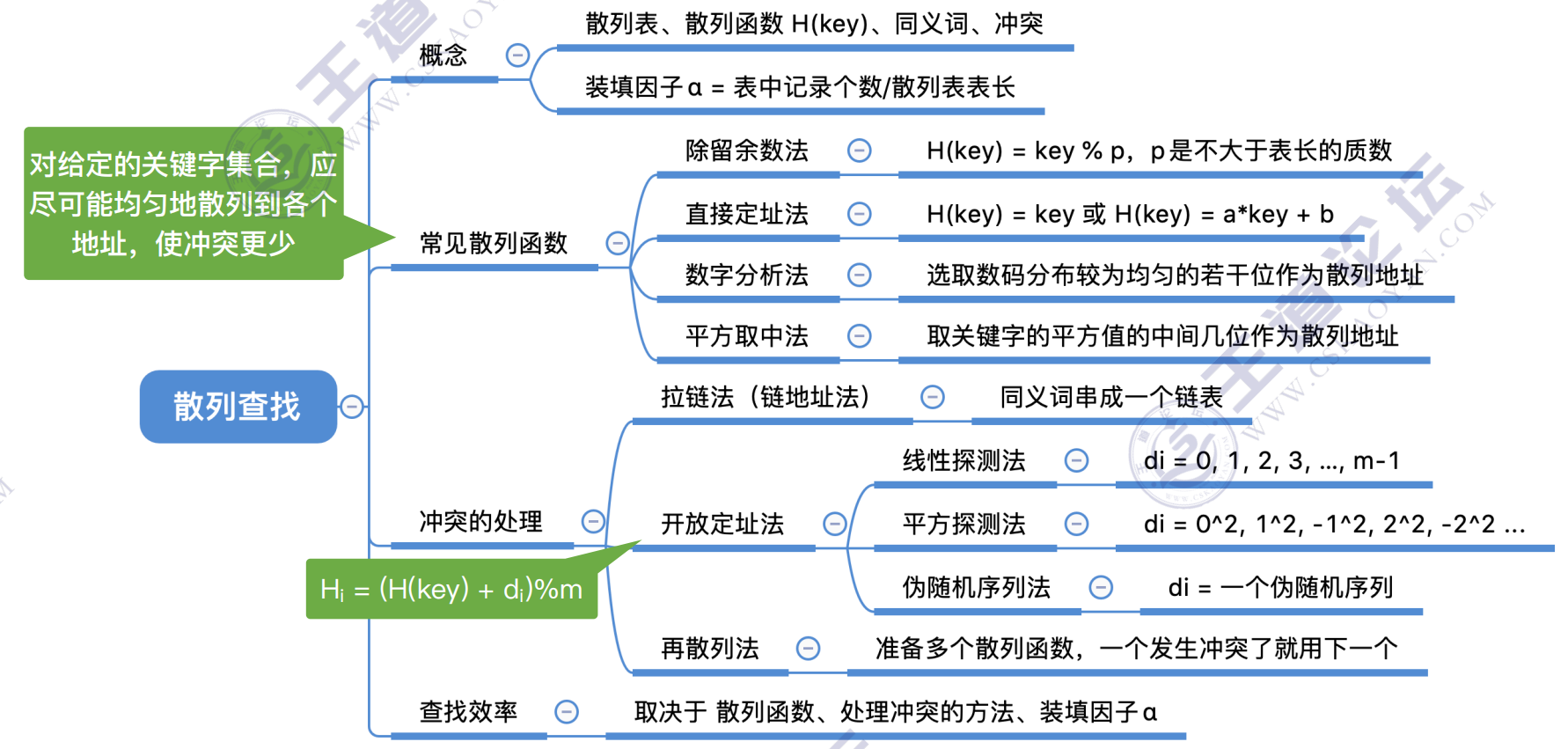
总结


 浙公网安备 33010602011771号
浙公网安备 33010602011771号