数据结构-二叉搜索树

二叉搜索树是一颗二叉树且满足性质:

设x是二叉树的一个节点。如果y是x左子树的一个节点，那么y.key ≤ x.key; 如果y是x右子树的一个节点，那么y.key > xkey。

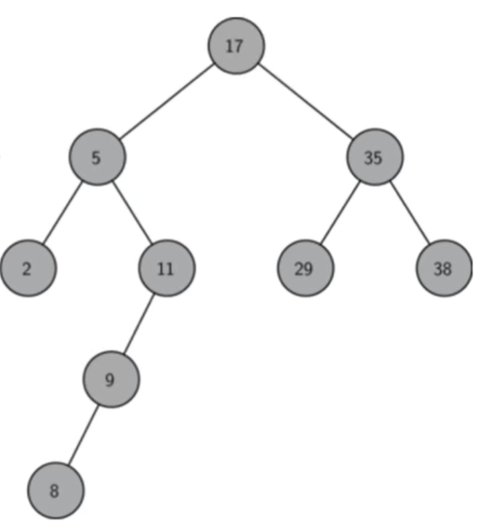
 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值，任意节点的左、右子树也是二叉搜索树，同样满足这个条件 

 

 二叉搜索树的操作:

• 查询
• 插入
• 删除

import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)
# 插入
    def insert_no_rec(self, val):  # 非递归写法
        p = self.root
        if not p:   # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild    # p指针指向p的左孩子
                else:   # 左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return
# 查询
    def query_no_rec(self, val):    # 非递归写法
        p = self.root
        while p:
            if p.data < val:
                p = p.rchild
            elif p.data > val:
                p = p.lchild
            else:
                return p
        return None
　　
　　# 删除时的各个情况
    def __remove_node_1(self, node):
        # 情况1：node是叶子节点
        if not node.parent:     # 如果是没有父亲的 根节点
            self.root = None
        if node == node.parent.lchild:  # node是它父亲的左孩子
            node.parent.lchild = None   # 将左孩子置为空
        else:   # 右孩子
            node.parent.rchild = None

    def __remove_node_21(self, node):
        # 情况2.1：node只有一个左孩子
        if not node.parent: # node为根节点时
            self.root == node.lchild
            node.lchild.parent = None
        elif node == node.parent.lchild:    # node在它父亲的左边并且有一个左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:   # node在它父亲的右边并且只有一个左孩子
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        # 情况2.2：node只有一个右孩子
        if not node.parent:
            self.root = node.rchild
            node.rchild.parent = None
        elif node == node.parent.lchild:    # node是它父亲的左孩子并且只有一个右孩子
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:                               # node是它父亲的右孩子并且只有一个右孩子
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent
　　 
　　# 删除 
    def delete(self, val):
        if self.root: # 不是空树
            node = self.query_no_rec(val)
            if not node: # 要删除的node不存在
                return False
            if not node.lchild and not node.rchild: # 1.叶子节点
                self.__remove_node_1(node)
            elif not node.rchild:   # 2.1 只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild:   # 2.2 只有一个右孩子
                self.__remove_node_22(node)
            else:                   # 3.两个孩子都有
                min_node = node.rchild
                while min_node.lchild:  # 只要左孩子不为空就一直找左孩子
                    min_node = min_node.lchild
                node.data = min_node.data  # 将node.data直接替换成最后找到的左孩子
                # 删除min_node
                if min_node.rchild:
                    self.__remove_node_22(min_node)
                else:
                    self.__remove_node_1(min_node)

li = list(range(50))
random.shuffle(li)
tree1 = BST(li)
# tree1.in_order(tree1.root)
node = BST(li).root     # node 指向根节点
print(tree1.query(node, 5).data)
tree1.delete(4)
# print(tree1.query_no_rec(4).data)
tree1.in_order(tree1.root)