栈-迷宫问题

给一个二维列表，表示迷宫（0表示通道，1表示围墙）。给出一条走出迷宫的路径

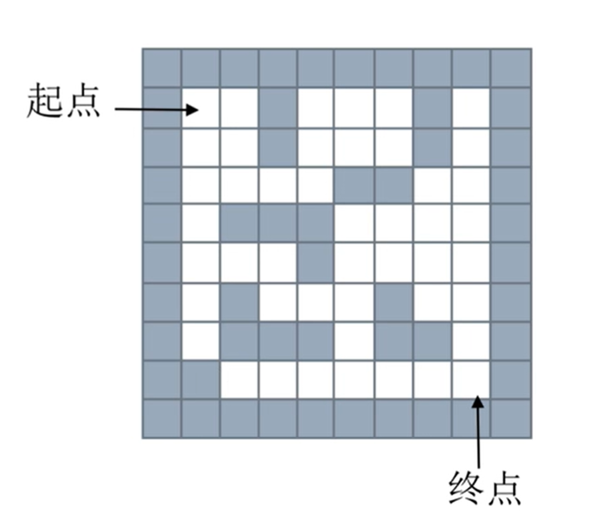
栈-深度优先搜索，回溯法思路：使用栈存储当前路径，从一个节点出发，任意找一个能走的点，当找到不能找的点时，退回上一个点寻找是否有其他方向的点（出栈）。

# 深度优先搜索 又称回溯法
maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x,y:(x+1,y),
    lambda x,y:(x-1,y),
    lambda x,y:(x,y-1),
    lambda x,y:(x,y+1)
]　　# 每一个点都有四个方向

def maze_path(x1,y1,x2,y2):　　# x1,y1表示起点，x2，y2表示终点
    stack = []　　
    stack.append((x1, y1))　　
    while len(stack)>0:　　# 只要栈不为空
        curNode = stack[-1] # 当前的节点
        if curNode[0] == x2 and curNode[1] == y2:　　# 走到终点了
            for p in stack:
                print(p)　　# 打印路径
            return True
        for dir in dirs: # x,y四个方向
            nextNode = dir(curNode[0], curNode[1]) # 二维元组
            if maze[nextNode[0]][nextNode[1]] == 0: 　　# 如果下一个节点能走
                stack.append(nextNode)　　# 则将下一个节点入栈
                maze[nextNode[0]][nextNode[1]] = 2 # 否则标记为2，2表示已经走过
                break
        else:
            maze[nextNode[0]][nextNode[1]] = 2
            stack.pop()　　# 退回
    else:
        print('没有路')
        return False

maze_path(1,1,8,8)