直方图规定化公式推导及代码实现
1. 概述¶
所谓直方图规定化,就是通过一个灰度映像函数,将原灰度直方图改造成所希望的直方图
理想情况下,直方图均衡化实现了图像灰度的均衡分布,对提高图像对比度、提升图像 亮度具有明显的作用。在实际应用中,有时并不需要图像的直方图具有整体的均匀分布,而 希望直方图与规定要求的直方图一致,这就是直方图规定化。它可以人为地改变原始图像直方图的形状,使其成为某个特定的形状,即增强特定灰度级分布范围内的图像
2. 公式推导¶
设有一张原始图像 A,已知其概率密度为$p_r(r)$,若对其进行直方图均衡化得到图像 $A’$,对应的变换函数为$T(i)$,则有:
$$ T(i)=\int _0^i p_r(r)dr $$设有一张目标图像 B,已知其概率密度为$p_u(u)$,若对其进行直方图均衡化得到图像 $B’$,对应的变换函数为$G(j)$,则有:
$$ G(j)=\int _0^j p_u(u)du $$
由上图,易知:
$$T(k)=s=G(q)$$显然,有:
$$ \int _k^{k+\triangle k}p_r(r)dr=\int _s^{s+\triangle s}1ds=\int _q^{q+\triangle q}p_u(u)du $$当:$\triangle k \rightarrow 0,\triangle s \rightarrow 0,\triangle q \rightarrow 0$,针对离散图像,则有:
$$A中灰度为k的像素数=B中灰度为q的像素数= A'中灰度为T(k)的像素数=B'中灰度为G(q)的像素数$$由于$A \rightarrow B$本质属于灰度变换,并不希望改变像素坐标,所以:
$$A中灰度为k的像素坐标=B中灰度为q的像素坐标= A'中灰度为T(k)的像素坐标=B'中灰度为G(q)的像素坐标$$综上:$$A'=B'$$
从而: $$ B=G^{-1}(B')=G^{-1}(A')$$
进而:$$B=G^{-1}[T(i)]$$
由于 $G$ 是变限积分,无法直接得到其逆变换
在工程应用中,一般图像灰度取值为0-255,由于目标图像的灰度直方图已知,即变换函数 $G$ 已知,就可以建立一张灰度0-255对应的映射表,对应的是 $B 与 B'$ 的映射关系

由于$A'=B'$,从而可以反推出目标图像 $B$
- 这种反推目标图像是一种近似估算
3. 代码实现¶
总结第二小节的理论公式,代码实现步骤为:
- 计算输入图像$A$的概率密度
- 对输入图像进行直方图均衡化得到$A'$
- 设置目标图像的概率密度函数$G$
- 构造概率密度函数$G$对应的0-255的灰度映射表
- 将$A'$对应灰度映射表得到目标图像$B$
计算输入图像的概率密度计算与直方图均衡化:
# 获取图像的概率密度
def get_pdf(in_img):
total = in_img.shape[0] * in_img.shape[1] #计算图片总像素数
return [ np.sum(in_img == i)/total for i in range(256) ] #求概率密度
# 直方图均衡化(核心代码)
def hist_equal(in_img):
# 1.求原始图像的概率密度
Pr = get_pdf(in_img)
# 2.构造输出图像(初始化成输入)
out_img = np.copy(in_img)
# 3.执行“直方图均衡化”(执行累积分布函数变换)
y_points = [] # 存储点集,用于画图
SUMk = 0 # 累加值存储变量
for i in range(256):
SUMk = SUMk + Pr[i]
out_img[(in_img == i)] = SUMk*255 #灰度值逆归一化
y_points.append(SUMk*255) #构造绘制函数图像的点集(非核心代码,可忽略)
return out_img.astype("int32"), y_points设置目标图像的概率密度函数:
# 生成多峰正态分布
# means 各峰均值
# stds 各峰标准差
# ampl 各正态分布幅值(和为1)
# bias 概率密度函数总体抬升量(若没有抬升量,容易造成图像过暗)
def gen_mul_norm_pdf(x, means, stds, ampl, bias):
pdf = np.zeros([256,], dtype=float)
for i in range(len(means)):
pdf_temp = ampl[i]*np.exp(-((x-means[i])**2)/(2*stds[i]**2))\
/(stds[i] * np.sqrt(2 * np.pi))
pdf = pdf + pdf_temp
pdf = pdf + bias #总体抬升概率密度,避免出现零值
pdf2 = pdf/np.sum(pdf) #由于做了抬升,所以要重新归一化
return pdf2.tolist()- 这里的函数可以根据输入图像进行确定
构造概率密度函数对应的0-255的灰度映射表:
# 构造目标图像的映射表(核心代码)
def gen_target_table(Pv):
table = []
SUMq = 0.
for i in range(256):
SUMq = SUMq + Pv[i]
table.append(round(SUMq*255, 0)) #四舍五入
return table将均衡化后的图像对应映射表从而得到目标图像:
为了简化编码,我们进一步简化映射规则:
- 映射表中若未找到某个数字,则直接取前一个逆映射值
- 映射表中若某个数字有多个逆映射值,默认取最大逆映射值
# 直方图规定化(核心代码)
def hist_specify(in_img=None):
# 1.拿到目标图像规定概率密度,并构造映射表
Pv = gen_mul_norm_pdf(np.arange(0,256,1),[38,191],[13,13],[0.93,0.07],0.002)
table = gen_target_table(Pv)
# 2.对原始图像做直方图均衡
ori_eq_img, T_points = hist_equal(in_img)
# 3.构造输出图像(初始化成输入)
out_img = np.copy(ori_eq_img)
# 4.执行“直方图规定化”(根据映射表,做逆映射 B'->B)
map_val = 0 # 逆映射值初始化为0
for v in range(256):
if v in ori_eq_img: # 存在于B'
if v in table: # 存在于映射表
map_val = len(table)-table[::-1].index(v)-1 #拿到指定值最后出现的索引
out_img[(ori_eq_img == v)] = map_val # 找不到映射关系时,取前一个映射值
return out_img, T_points, table, Pv进行数字图像处理:
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
# 读入原图
gray_img = np.asarray(Image.open('./image/mars_moon_phobos.tif').convert('L'))
# 对原图执行“直方图规定化”
out_img, T_pts, G_pts, spec_hist = hist_specify(gray_img)
# 创建1个显示主体,并分成6个显示区域
fig = plt.figure()
ax1, ax2, ax3 = fig.add_subplot(231), fig.add_subplot(232), fig.add_subplot(233)
ax4, ax5, ax6 = fig.add_subplot(234), fig.add_subplot(235), fig.add_subplot(236)
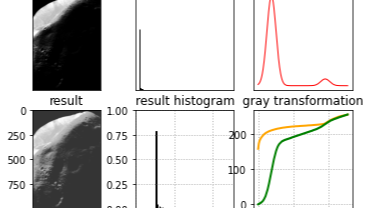
# 窗口显示:原图,原图灰度分布,规定PDF,结果图像,结果图像灰度分布,对应变换函数
ax1.set_title('origin', fontsize=12)
ax1.imshow(gray_img, cmap='gray', vmin=0, vmax=255)
ax1.axes.xaxis.set_visible(False)
ax1.axes.yaxis.set_visible(False)
ax2.grid(True, linestyle=':', linewidth=1)
ax2.set_title('origin histogram', fontsize=12)
ax2.set_xlim(-10, 255) # 设置x轴分布范围
ax2.set_ylim(0, 1) # 设置y轴分布范围
ax2.hist(gray_img.flatten(),bins=255,density=True,color='black',edgecolor='black')
ax2.axes.xaxis.set_visible(False)
ax2.axes.yaxis.set_visible(False)
ax4.set_title('result', fontsize=12)
ax4.imshow(out_img, cmap='gray', vmin=0, vmax=255)
ax5.grid(True, linestyle=':', linewidth=1)
ax5.set_title('result histogram', fontsize=12)
ax5.set_xlim(0, 255) # 设置x轴分布范围
ax5.set_ylim(0, 1) # 设置y轴分布范围
ax5.hist(out_img.flatten(),bins=255,density=True,color='black',edgecolor='black')
# 窗口显示:绘制规定概率密度函数
ax3.set_title("regulation pdf", fontsize=12)
ax3.grid(True, linestyle=':', linewidth=1)
ax3.plot(np.arange(0, 256, 1), spec_hist, color='r',lw=1)
ax3.axes.xaxis.set_visible(False)
ax3.axes.yaxis.set_visible(False)
# 窗口显示:绘制对应的灰度变换函数
ax6.set_title("gray transformation", fontsize=12)
ax6.grid(True, linestyle=':', linewidth=1)
ax6.plot(np.arange(0, 256, 1), T_pts, color='orange',lw=2)
ax6.plot(np.arange(0, 256, 1), G_pts, color='green', lw=2)
plt.show()
可以看到有效增强了实验图像的对比度
利用已知的图像直方图分布,从而对输入图像进行处理,是直方图规定化的应用
已知常规环境下的图像,对异常情况下的图像进行处理,比如去除有雾的图像等


 基于Python讲述直方图规定化公式推导及代码实现
基于Python讲述直方图规定化公式推导及代码实现

 浙公网安备 33010602011771号
浙公网安备 33010602011771号