复杂度分析

复杂度分析是学习数据结构与算法的前提。

事后统计法

通过监控、统计把代码跑一遍的方法。

• 局限性：
  1. 依赖测试环境。比如 i9 和 i3 的 cpu 跑同一段代码。
  2. 受数据规模影响大。比如已排序好的数组和未排序好的数组。

大 O 复杂度表示法

\(T(n) = O(f(n))\)

T(n)表示代码的执行时间，f(n)表示每行代码的执行次数总和，O 代表一个函数，表示 f(n)和 T(n)之间关系成正比。

• 表示代码执行时间随数据规模增长的变化趋势，并不表示真正的执行时间。
• 只关注循环执行次数最多的一段代码，通常会忽略掉公式中的常量、低阶、系数。

加法法则：总复杂度等于量级最大的那段代码的复杂度

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }
   // 100

   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }
    // n

   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum_3 = sum_3 +  i * j;
     }
   }
   // n*n
  // 最终为 O(n*n)
   return sum_1 + sum_2 + sum_3;
 }

乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

int cal(int n) {
	int ret = 0;
	int i = 1;
	for (; i < n; ++i) {
	 ret = ret + f(i);
	}
	// n
}

int f(int n) {
	int sum = 0;
	int i = 1;
	for (; i < n; ++i) {
	  sum = sum + i;
	}
	//
	return sum;
}

// 最终为 O(n*n)

多个数据规模情况

计算出各个数据的复杂度并遵循加法、乘法法则。

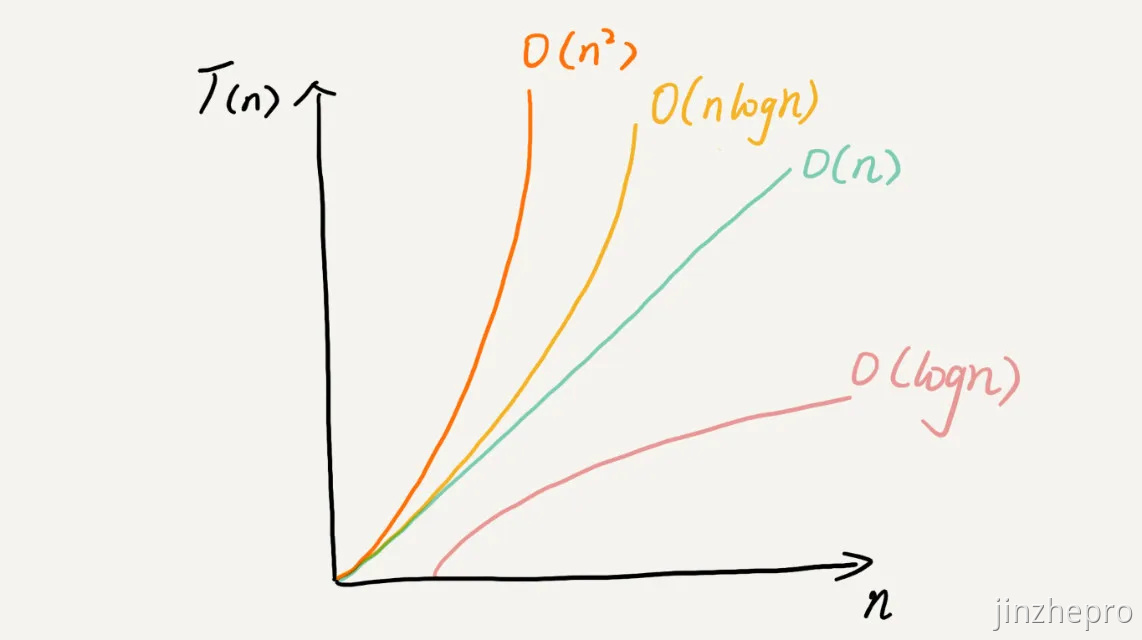
复杂度量级

• 常量阶 \(O(1)\)
  • 一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是\(Ο(1)\)。
• 对数阶 \(O(log_n)\)
  • 等比数列
• 线性阶 \(O(n)\)
• 线性对数阶 \(O(nlog_n)\)
• k 次方阶 \(O(n^k)\)
• 指数阶 \(O(2^n)\)
• 阶乘阶 \(O(n!)\)

最好、坏情况时间复杂度

变量 x 可以出现在数组的任意位置: 出现在第一个，复杂度为 O(1)[最好情况]；出现在最后一个，复杂度为 O(n)[最坏情况]。

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}

平均情况时间复杂度

将概率加入到计算中，计算查找每个值的概率

均摊时间复杂度

均摊时间复杂度就是一种特殊的平均时间复杂度