[深度学习] 基本概念介绍汇总

0. 前言

从这学期期末考完开始，我们的大创项目算是正式开场了，距离中期答辩过去近一个月。

这篇文章大概是用来记录一下在这几天初期学到的各种东西，毕竟一个全新的领域，太多概念与术语。

章节之间并非并列关系，从所需的基础数学知识，到各种优化方法，到机器学习领域，到卷积神经网络，到目标检测算法以及评价指标，其实是更像递进关系。

因为还在学习过程中，尽管许多知识还是比较轻描淡写地带过了，但中间还是可能有各种疏漏，还待慢慢补充与修改。

 

1. 卷积

1.1. 点积

对于两个向量 u = [u₁, u₂, ..., u_n], v = [v₁, v₂, ... v_n]，其点积为：

u · v = u₁ * v₁ + u₂ * v₂ + ... + u_n * v_n

1.2. 卷积

对于两个离散信号 f, g，其卷积结果为一个信号倒序后在不同位置和另一个信号中一段相同长度的部分求点积的集合。

假设前者信号为 f，后者为 g，则 f 又被称为卷积核（Kernel）。f 和 g 可以交换，结果不会变化。

下面为一个一维信号求卷积的例子。

 

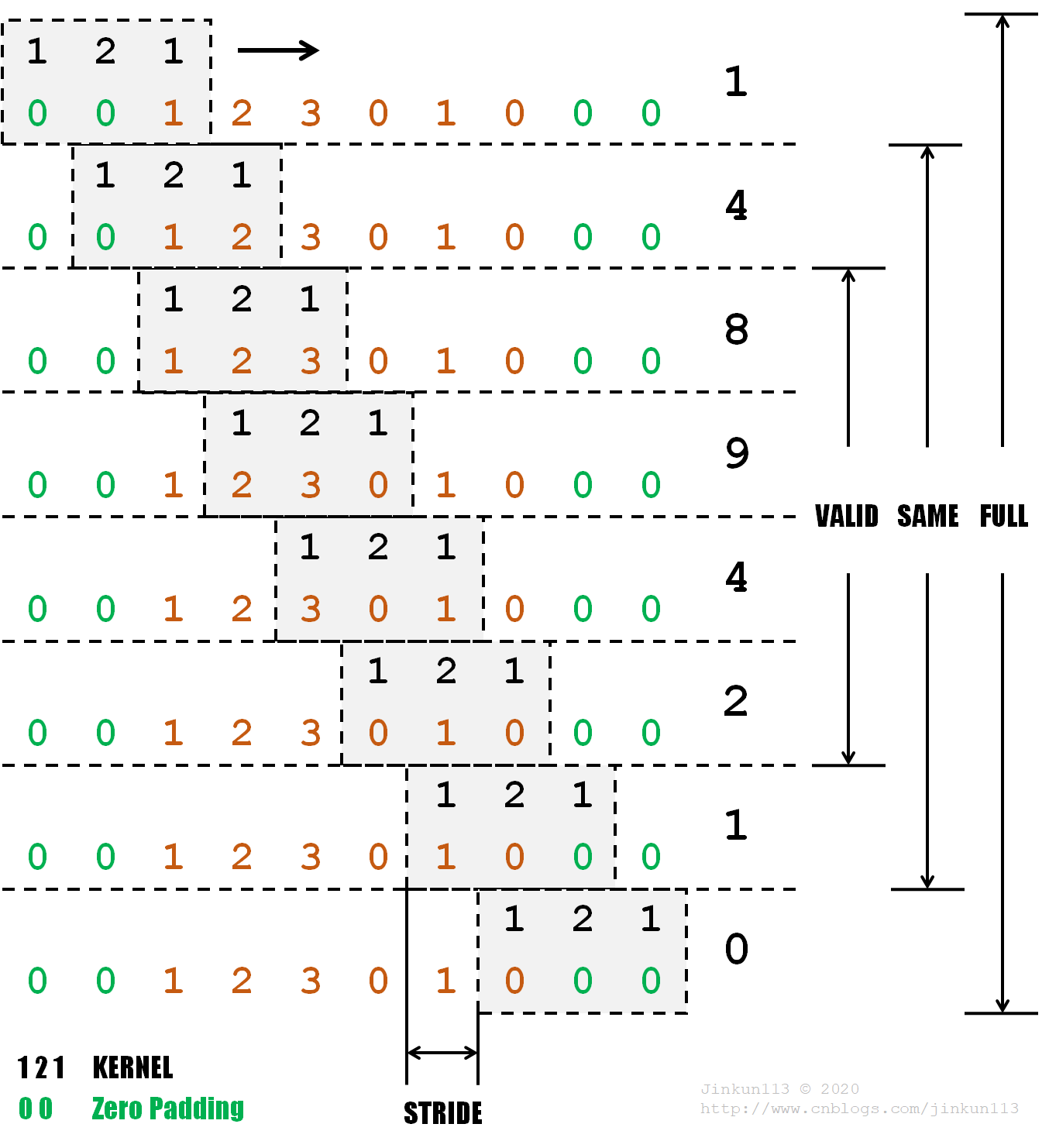
其中卷积核信号 f 为 [1, 2, 1]，倒置后仍为 [1, 2, 1]，信号 g 为 [1, 2, 3, 0, 1, 0]。

比如第一次卷积运算过程为：

1 * 0 + 2 * 0 + 1 * 1 = 1，即结果为 1。

注意到在待卷积信号 g 前后分别加上了 2 个 0，它们被称为零填充（Zero Padding），作用在下面会提到。

卷积核每次移动的距离叫做步长（Stride），本例步长为 1。

卷积有三种类型，设卷积核信号 f 长度为 n，待卷积信号 g 长度为 m，有：

① Valid

不对信号 g 进行零填充而求卷积，即卷积核起初与待卷积信号由左对齐至右对齐，卷积长度为 m - n + 1；

② Same

对信号 g 的边缘共添加 n - 1 个 0，使得卷积结果与信号 g 长度一致，即 m；

③ Full

对信号 g 的边缘再添加 n - 1 个 0，使得卷积核能够划过的位置最大，即由卷积核右边缘与待卷积信号左边缘对齐至卷积核左边缘与待卷积信号右边缘对齐，卷积长度为 m + n - 1。

二维卷积同理。

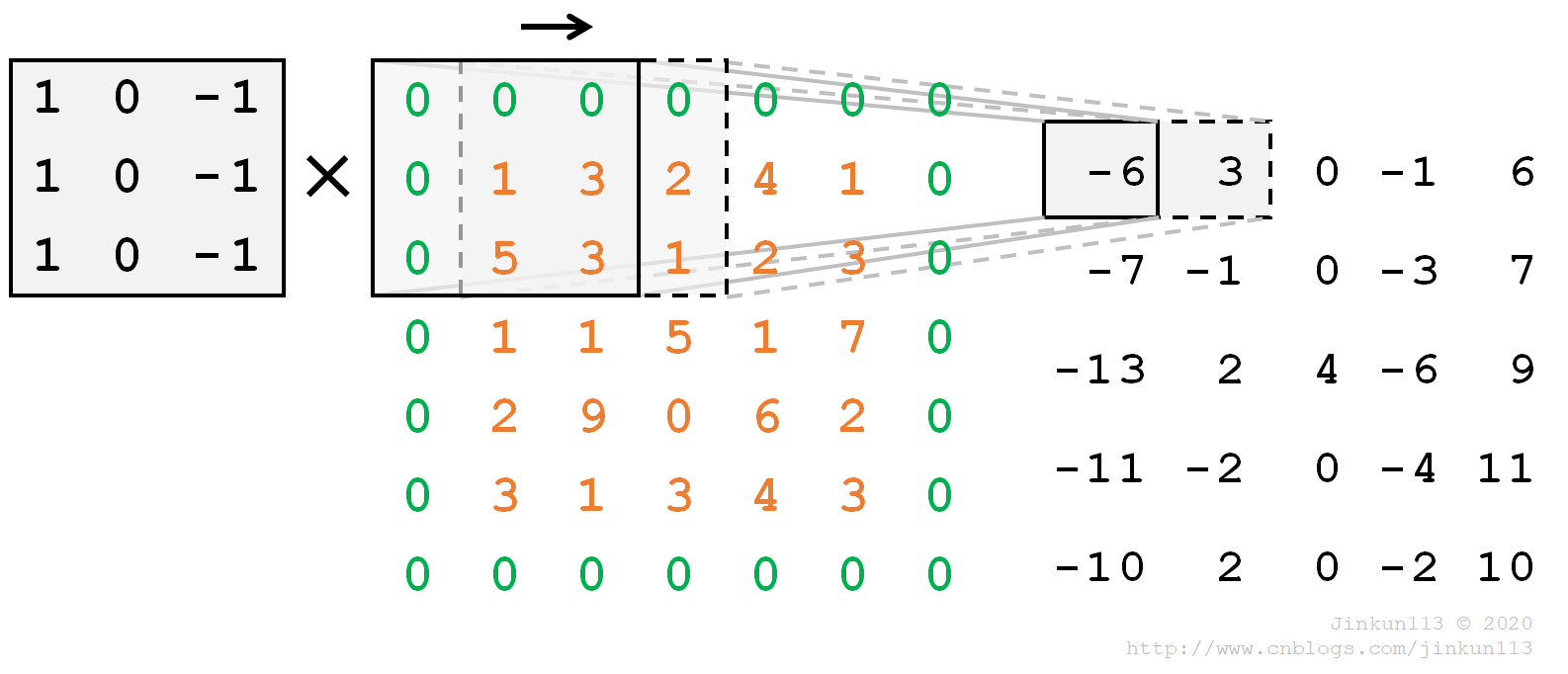计算方法

 

2. 数学优化基础

2.1. 梯度下降算法

重复 ① 与 ②：

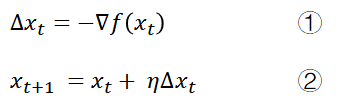
直到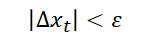

用于寻找最小值

𝜂 为一个系数，称为学习率（Learning Rate），控制更新时的步长大小。

2.2. 牛顿法

略

2.3. 超参数

超参数指在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。

2.3.1. 优化器（Optimizer）

略

2.3.2. 学习率（Learning Rate）

略

2.3.3. 激励函数（Activation Function）

激励函数的作用是让神经网络模型能够逼近非线性函数。

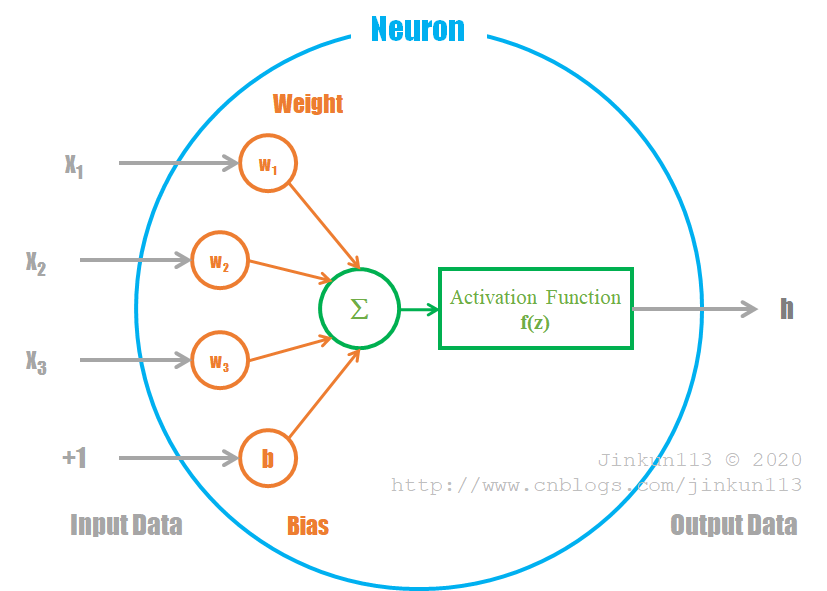
① Sigmoid 函数

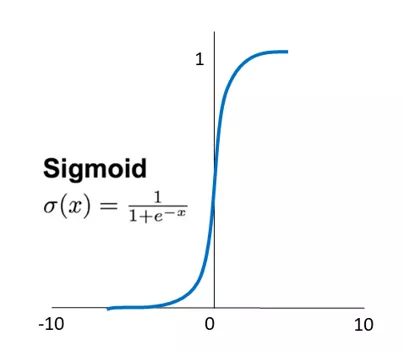
② tanh 函数

 

③ Softmax

将输出转换为概率

令 z = (wx + b) / 2，则可以化为：

f(x) = g(z) = 1 / (1 + e^-2z) = e^z / (e^z + e^-z)

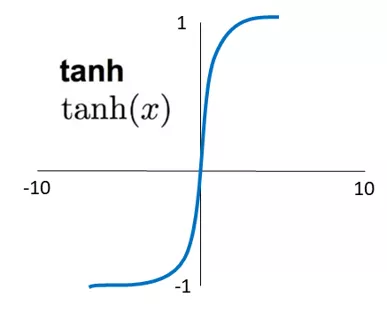
④ ReLU 线性整流函数

 

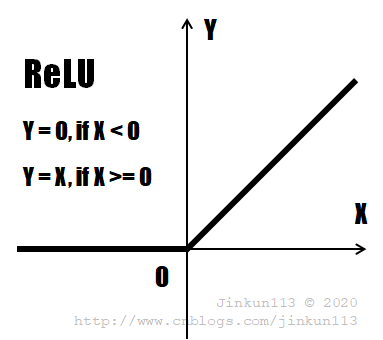
上述 Sigmoid 和 tanh 激励函数容易导致多层神经网络模型在训练过程中出现梯度消失的现象，而 ReLU 则不会出现这种问题。

线性整流函数（ReLU, Rectified Linear Units），经常被用于多层神经网络的中间层，且其计算速度更快，它只需要判断神经元的输出值是否小于 0，能够很好地帮助训练快速收敛，同时保证稀疏性。

Leaky ReLU：将 x < 0 部分改成一个斜率很小的一次函数；

Parametric ReLU（PReLU）：斜率值成为一个可优化的参数；

Softplus：平滑版 ReLU，公式为 f(x) = ln(1 + e^x)

2.3.4. 损失函数

优化问题只是一个单纯的函数值最小化问题，和机器学习关联起来，靠的是如何定义要优化的函数，从优化角度来讲这个函数叫做目标函数，或损失函数（Loss Function）。

回归任务 二分类任务 多分类任务

【待补充】

2.3.5. 其他超参数

Epoch：一代训练，即使用训练集的全部数据对模型进行的一次训练。主要看损失是否收敛在一个稳定值，如果是，则当前设置的 Epoch 值最佳。Epoch 太小可能导致欠拟合；Epoch 太大可能导致过拟合。

Batch：一批数据，即训练集的一小部分样本，使用它们对模型权重进行一次反向传播的参数更新。BatchSize 为 Batch 的大小，一般来说不能太大也不能太小。

Iteration：一次训练，即使用一个 Batch 数据对模型进行一次参数更新的过程。

 

3. 机器学习基础

【待补充】

3.1. 数据增强（Data Augmentation）

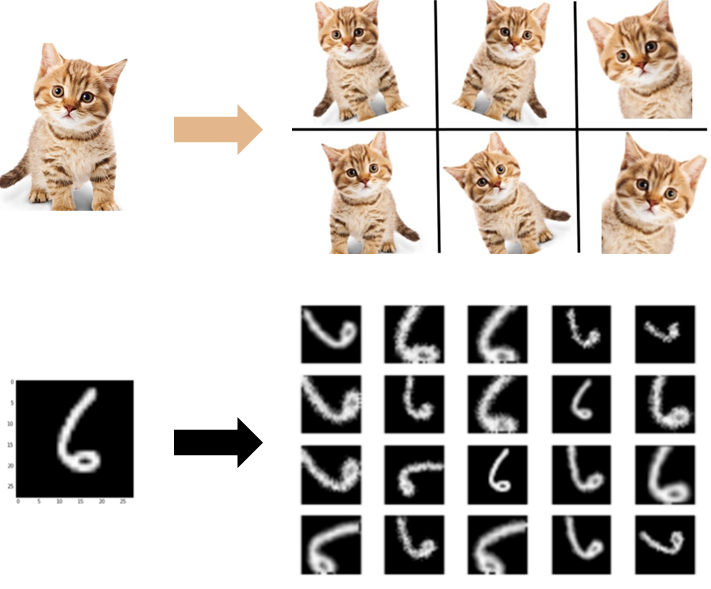
解决样本数量不均衡的问题，同时提升算法的鲁棒性。

3.2. 过拟合与欠拟合

衡量一个机器学习算法的优劣，最直接的方法是衡量算法预测与测量数据的误差。对于训练数据，损失函数是衡量标准；而对于预测数据，算法对其做出准确预测的能力称为泛化（Generalization）能力。

过拟合（Overfitting），指为了得到一致假设而使假设变得过度严格，其反义词为欠拟合（Underfitting）。如下图所示。

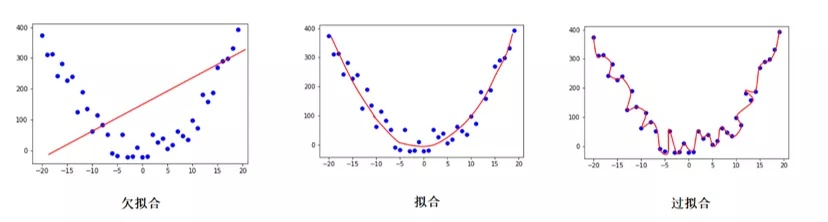
一个更贴近生活的理解是，高中生 kk 刷了一大堆理综的题目，他对那些做过的题滚瓜烂熟，但一到考试碰到类似却不同的题一脸懵逼，也可以认为是一种过拟合。

模型的拟合能力通常被称为 Capacity。对于卷积神经网络，过拟合一般指经过训练得到的超参数与训练数据集匹配度过高，而测试数据集的结果精确度远低于训练数据集，即泛化能力弱。

3.3. 正则化

在损失函数上加入一个约束项，以提高泛化能力。

① L2 正则化

L2 正则化 / 规范化（L2 Regularization），又被称为权重衰减（Weight Decay）。

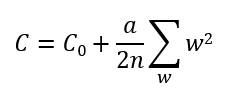
C 为当前神经网络的损失，C₀ 为之前的损失，a 为惩罚（penalty）因子。

② L1 正则化

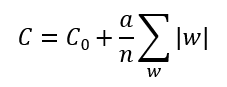
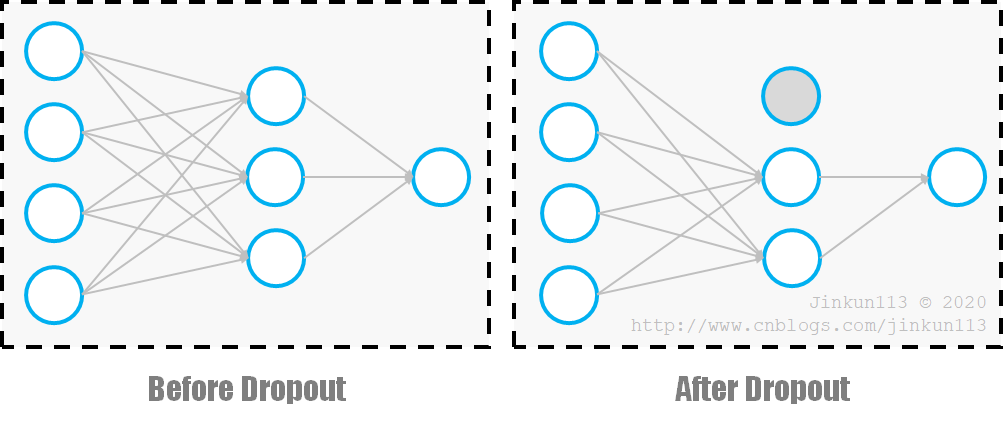
3.4. 随机失活

随机失活（Dropout），底层思想是把多个模型的结果放在一起，每次梯度迭代中使隐藏层中的每个神经元以一定概率 p 不被激活，比如：

3.5. 监督学习

① 监督学习

监督学习（Supervised Learning），指用来训练网络的数据所对应的输出是已知的，其可能是一个类别标签，可能是一个或多个值。

② 无监督学习

无监督学习（Unsupervised Learning），指数据没有被标记，即类别未知，而完全由计算机自行判断。一般适用于缺乏先验知识或进行人工标注的成本过高的情况。

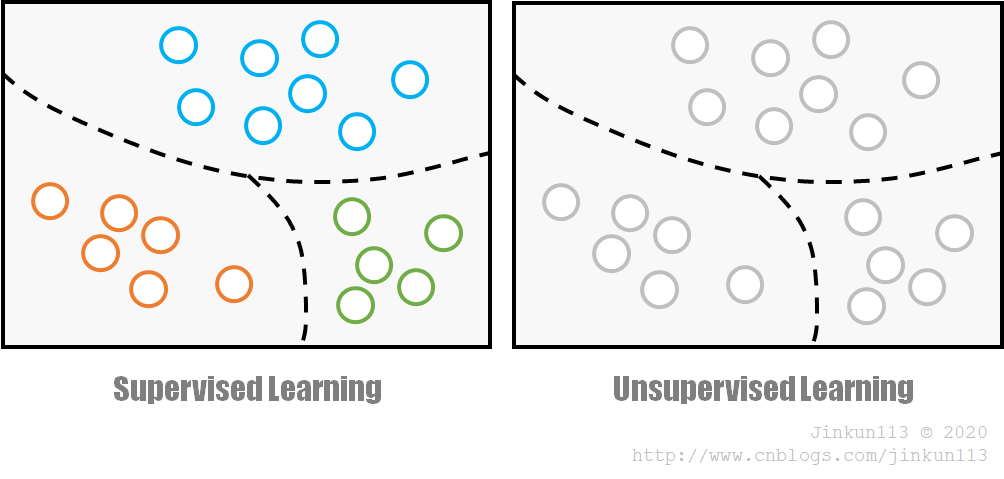
在无监督学习下对样本的划分通常被称为聚类（Clustering），常见方法有 K-means，混合高斯模型（GMM）等。

③ 半监督学习

半监督学习（Semi-Supervised Learning, SSL），是监督学习与无监督学习相结合的一种学习方法，在使用尽量少的工作从事人员的前提下，又能够带来比较高的准确性。

也有弱监督学习（Weakly Supervised Learning）的叫法。

 

 

4. 卷积神经网络

4.1. FCNN 全连接神经网络

全连接神经网络（FCNN, Fully Connected Neural Network）是最朴素的神经网络，其参数最多，计算量最大。一般可用下图表示：

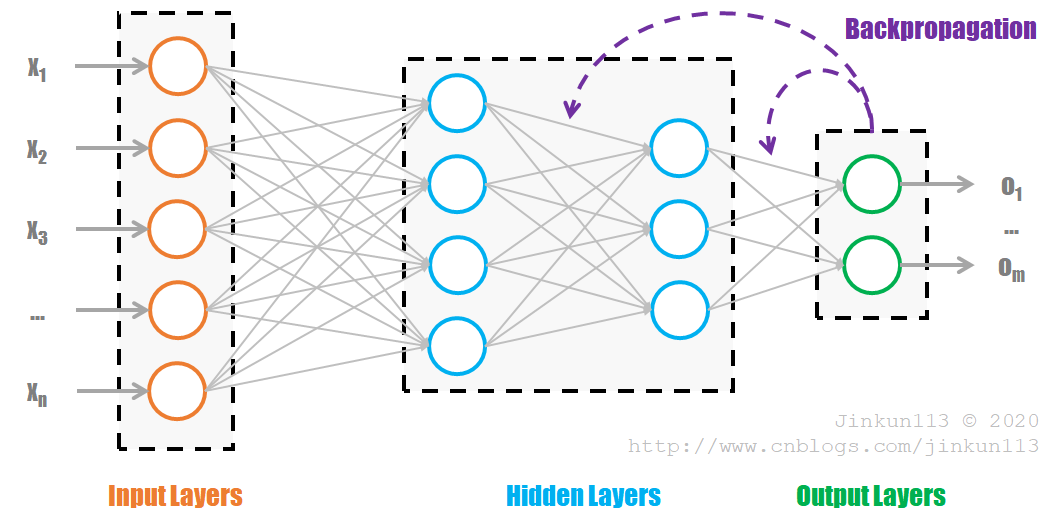
网络由若干层组成，第一层为输入层（Input Layers），最后一层为输出层（Output Layers），中间为隐藏层（Hidden Layers）。每一层都以前一层的输出作为输入，再经过计算输出到下一级。每一个圆圈为一个神经元（Neuron），内部为如下的计算组合：

① z = wx + b，最小化损失函数（前向传播）【待修改】，其中 w 为权值（Weight），b 为偏置（Bias）；

② z -> f(z)，激励函数（Activation Function），将输出值域压缩至 (0, 1)，即数据归一化（Normalization），在全连接网络中一般使用的是 Sigmoid 激励函数。

神经网络的训练是有监督的学习，对于输入值 X，有着与之对应的实际值 Y，而输出值 Y' 与实际值 Y 之间的损失 Loss 即反向传播的内容。整个网络的训练过程就是不断缩小 Loss 的过程。

4.2. CNN 卷积神经网络

FCNN 用于所有层级之间都是全部相连的，结构复杂，收敛缓慢，效率很低，会处理大量的冗余数据。而 CNN 是解决效率问题的一种办法。

卷积神经网络（CNN, Convolutional Neural Network），相比 FCNN 结构增加了卷积层（Convolutional Layers），池化层（Pooling Layers），输出层由全连接层和 Softmax 层构成。

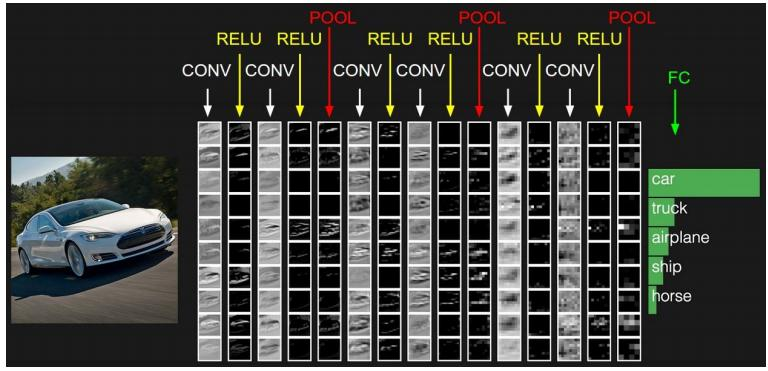
① 卷积层

卷积层至少有 1 层，之间为局部连接，且权值共享，大幅减少了 (w, b) 的数量，加快训练速度。卷积层的作用，简单来说就是通过压缩提纯，来提取特征。

对于 CNN 而言，权值 w 即卷积核。和卷积核做卷积得到的结果叫做特征图（Feature Map）。

在卷积核后再加上激励函数。

② 池化层

一般来说，卷积层后面都会加上一个池化层，它是对卷积层的进一步特征抽样，用于压缩数据与参数量，减小过拟合（Overfitting）。其具体操作与卷积层基本相同，但只取对应位置的最大值与平均值（最大池化、平均池化）。

池化过程强调特征不变性。比如在图像处理时，一张狗狗的图像被缩小一倍后我们还能看出这是一只狗狗，那么说明这种图像在压缩时保留了狗狗的特征，而移除了无关紧要的信息。

下图为一个池化的例子，卷积核大小为 2 * 2，步长为 2，采用最大池化法，得到如下结果。

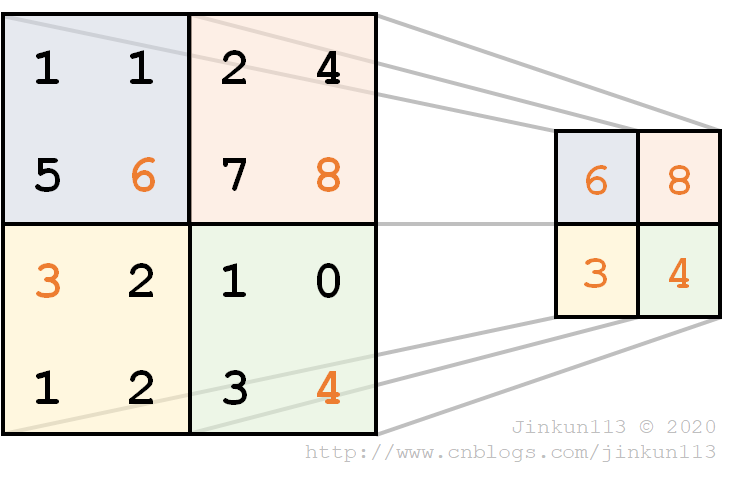
卷积层用来模拟对特定图案的响应，池化层模拟感受野（Receptive Field）。感受野的定义是卷积神经网络每一层输出的特征图上的像素点在输入图片上映射的区域大小。

（感受野这个翻译，初听感觉很奇怪，后来了解到是直接照搬的生物学术语）

③ 通道

无论是输入还是中间产生的特征图，通常并不是单一的二维图，而是多个图组成的，我们称每一张图为一个通道（Channel）。计算机的图像表示中，通道是一个非常基础的概念，比如一幅彩色图像通常由红色（R），绿色（G），蓝色（B）三个通道构成，即 RGB 图像。

4.3. 其他神经网络

 

4.4. 卷积神经网络发展

4.4.1. LeNet

LeNet 是第一个卷积神经网络。输入图片为 28 * 28 单通道灰度图。

4.4.2. AlexNet

输入图片为 256 * 256 的三通道彩色图片，数据增强手段包含随机位置裁剪，包含三张 224 * 224 的子区域，则输入维度为 3 * 224 * 224。

由于当时 GPU 不够强大，AlexNet 在卷积时采用分组的方法，以减少计算量且方便并行。

4.4.3. GoogLeNet

GoogLeNet 由 Google 发表在 CVPR2015 的《Going Deeper with Convolutions》中，其层数推进到了 22 层，跳出了 AlexNet 的基本结构，创新性地提出了构建网络的单元 Inception 模块。

Inception 结构

批处理规范（BatchNorm）

1 * 1卷积

ResNet

残差网络

4.4.4. 常用框架

① TensorFlow，Google 开发的深度学习框架

② Torch，Facebook 卷积神经网络工具包，还有专用于 Python 的 PyTorch

③ Caffe，不太了解

 

5. 目标检测算法

滑窗法（Sliding Window）

PASCAL VOC 

mAP

交并比

R-CNN

SPP ROI Pooling Fast R-CNN

RPN Fater R-CNN

YOLO SSD

 

6. 分类与检测的评价指标

6.1. P, R, F-Measure

假设图中有一只狗狗和一只猫猫，且当前关注目标为狗狗，则：

狗狗是正类（Positive）；猫猫是负类（Negative）。

将狗狗标记为狗狗，或将猫猫标记为猫猫，则预测结果正确（True）；

将狗狗标记为猫猫，或将猫猫标记为狗狗，预测结果错误（False）。

所以这四类情况可以总结为：

TP - 正类预测为正类，即将狗狗标记为狗狗

FN - 负类预测为负类，即将狗狗标记为猫猫

FP - 正类预测为负类，即将猫猫标记为狗狗

TN - 负类预测为正类，即将猫猫标记为猫猫

① Precision 精确率（查准率）

精确率 P = TP / (TP + FP)，正确预测为正类的个数占所有预测为正类的个数的比例，即所有标记为狗狗的图片中确实为狗狗的比例。

② Recall 召回率（查全率）

召回率 R = TP / (TP + FN)，正确预测为正类的个数占所有实际为正类的个数的比例，即所有狗狗中被标记为狗狗的比例。

③ F₁

Precision 体现是否找得对，Recall 体现是否找得全，两者通常相互影响，尽管理想情况下是两者均达到较高的理想值，但实际上一个越高另一个也就越低，所以一般只能根据实际的需求进行取舍。而如果在两者都有较高需求时，可以使用两者的权衡值来衡量。

F1 值是 Precision 和 Recall 的调和平均值，计算方式如下：

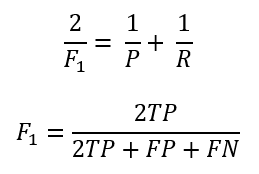
这种方法被称为 F-Measure，是检索领域很常用的评价标准。

④ F_β

F₁ 指标认为 P 和 R 是同等重要的，而当我们需要一个倾向时，可以使用 F_β。β 表示 R 的权重为 P 的 β 倍，则计算方式为：

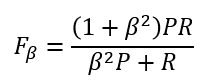
⑤ Accuracy 准确率

应该是没有一个比较统一的定义。(TP + TN) / (TP + FN + FP + TN) 算是一个定义方式，正确预测的个数占所有目标的个数的比例，即所有狗狗和猫猫分别被标记为狗狗和猫猫占所有狗狗和猫猫的比例。

上述概念推荐使用英文来表述，中文往往容易导致混淆。

6.2. mAP

上述 P, R, F-Measure 存在单点值局限性。为了更能反映全局性能，我们引入一个新的指标平均精确度均值（mAP, mean Average Precision），其规范定义如下：

 

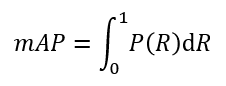
即 P - R 曲线与 x = 0, y = 1 包含的面积。

但在数据比较离散的情况下，也可以简单粗暴地把各个不同召回率上的精确率相加再求平均值，也是一种计算方式。

6.3. ROC & AUC

ROC 和 AUC 也是评价分类器的指标。还是以上述猫猫狗狗二分类，且关注狗狗为例。

观测者操作特性（ROC, Receiver Operating Characteristic），关注两个指标：

① TPR（True Positive Rate）

TPR = TP / (TP + FN)，即上述召回率，不再解释

② FPR（False Positive Rate）

FPR = FP / (FP + TN)，将负类错误预测为正类的个数占负类的个数的比例，即所有猫猫中被标记为狗狗的比例。

ROC 的分析工具 —— ROC 曲线（ROC Curve），即将 FPR 作为横坐标，TPR 作为纵坐标，它是一条经过 (0, 0), (1, 1)，且其余部分均在 y = x 上方的曲线，它与 x = 1, y = 0 包围的面积越大，说明表现越佳，这个值被称为 AUC（Area Under ROC Curve）。

6.4. MR-FPPI

漏检率曲线（MR-FPPI, Miss Rate Sgainst False Positives per Image）是目标检测中一个评估性能的指标，在 CVPR2009《Pedestrian Detection: A Benchmark, P. Dollar》中首次提出，如下图：

 

 

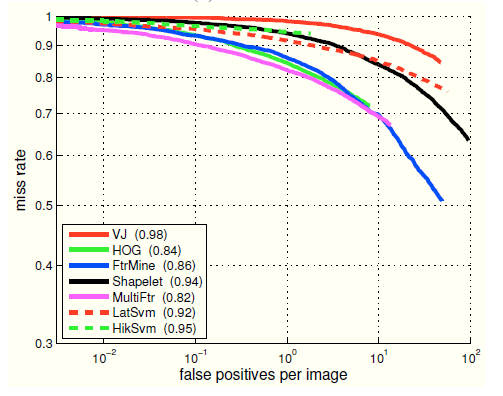
漏检率（Miss Rate, MR）与召回率是相对应的，即 Miss Rate + Recall Rate = 1，即所有狗狗中没有被标记为狗狗的比例。

MR-FPPI 适用于检测问题，而前面提到的 P-R 曲线，ROC 曲线更适用于分类问题。

6.5 IoU 系列

通常情况下，将一个目标完全正确地标记出来是不现实的。所以，我们引入一个新的参数交并比来判定。

① IoU

交并比（IoU, Intersection over Union），表示预测边框与实际边框的交集面积与并集面积的比值。如下图：

 

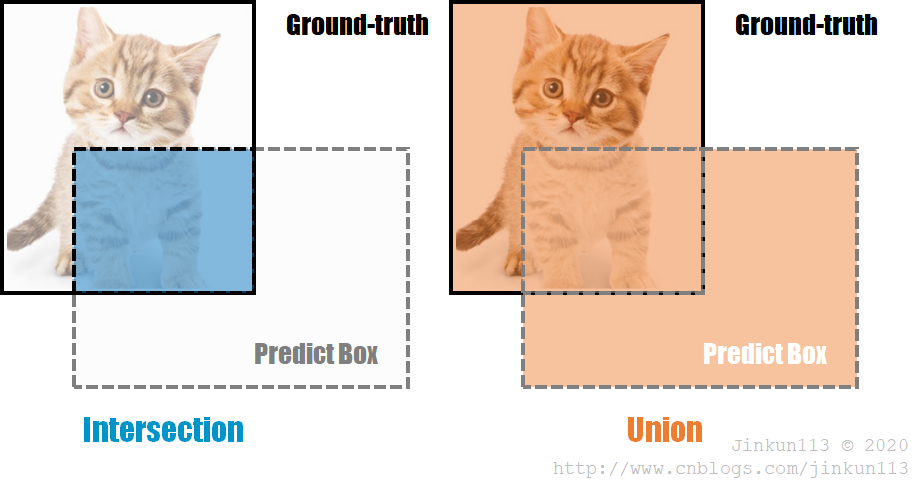
IoU 可以反映出预测框（Predict Box）与真实框（Gound-Truth）的检测效果。一个预测框被认为是正确结果（TP），一般需要满足与目标物体的真实框重合度（IoU）超过一个阈值（一般为 50%），否则为错误结果（FP）。

但它并不完美。如果将其作为损失函数，下列情况并不能很好反映出实际存在的问题：

> 如果两个框没有相交，根据定义，IoU = 0，则完全无法体现出框之间的距离。此时 Loss 值为 0，无梯度回传，无法进行学习训练；

> 无法区分对齐方式，精准反映实际重合效果。比如下列三个图像，IoU 值相等，但从左至右明显重合效果越来越差。

 

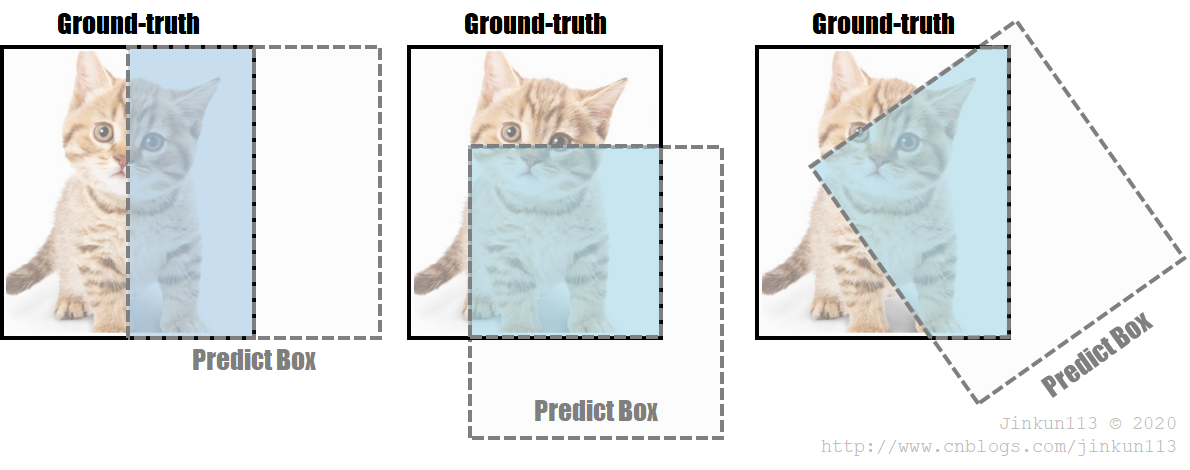
② GIoU

广义交并比（GIoU, Generalized-IoU），在 CVPR2019《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》中首次提出。论文提出直接把 IoU 设为回归的 Loss 值，计算公式如下：

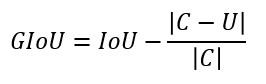
其中，C 表示两个框的最小闭包区域面积，如下图所示：

 

即等价于原 IoU 值减去图中深紫色区域。其取值范围为 [-1, 1]，是 IoU 的下界，当且仅当两个框完全重合时，IoU = GIoU = 1。

作为损失函数，L_GIoU = 1 - GIoU，满足损失函数的基本要求。

回到上面的三张图，其 IoU 和 GIoU 的值分别为：

 

③ DIoU

距离交并比（DIoU, Distance-IoU），相比 GIoU，它还考虑了框之间的距离、尺度，使得预测框回归变得更加稳定，不会出现发散问题。

 

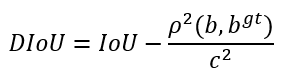
其中，b, b^gt 表示预测框与真实框的中心点，ρ 表示计算两个中心点之间的欧几里得距离；c 表示两个框的最小闭包区域的对角线距离。如下图所示：

 

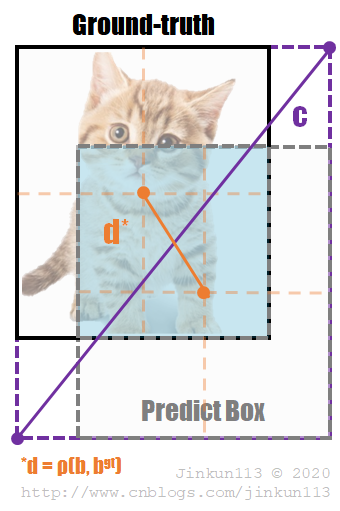
DIoU 可以直接最小化两个框的距离，因此比 GIoU 收敛快得多。对于两个框在水平或垂直方向的情况，DIoU 可以使回归非常快，而 GIoU 几乎退化为 IoU。

DIoU 还可以替换普通的 IoU 评价策略，应用于非极大值抑制（NMS, Non-Maximum Suppression）中，使得结果更加合理有效。

④ CIoU

完整交并比（CIoU, Complete-IoU），考虑到 Boundingbox 回归三要素中的长宽比还没被考虑，CIoU 在 DIoU 的基础上增加了惩罚因子。

暂略。

 

产品量化（product quantization）
修剪（pruning）
向量量化（vector quantization）
填充（padding）
乘加操作（Mult-Adds）
矩阵乘法（GEMM）
异步梯度下降（asynchronous gradient descent）
RMSprop
side heads
标签平滑（label smoothing）
叉积（cross product）
斯坦福狗狗数据集（Stanford Dogs dataset）
早停法（early-stopping）
建议框（proposal boxes）
三重损失（triplet loss）

方法：
扁平化网络（Flattened networks）
分解网络（Factorized Networks）
结构化转换网络（structured transform networks）
深度卷积网（deep fried convents）
低位网络（low bit networks）
蒸馏法（distillation）

 

双流

编码解码

注意力机制

Focus Loss

BoundingBox

Anchor

ONE / TWO STAGE

 

参考：

https://zhuanlan.zhihu.com/p/107822685

https://www.jianshu.com/p/22c50ded4cf7?from=groupmessage

https://www.cnblogs.com/skyfsm/p/6790245.html

https://blog.csdn.net/weixin_38145317/article/details/89310404

https://zhuanlan.zhihu.com/p/94799295