树状数组 & Trie树
md,我宣布线段树造福人类!!!
树状数组
需要满足结合律(交换顺序和左右分开算都是可以的)和可差分性(如果乘法的时候需要每个数都有逆元)。没有办法解决最大值(好像?)
大部分树状数组能够解决的题目都可以用线段树解决(但是老师说有些人丧心病狂会卡线段树)
结构图:
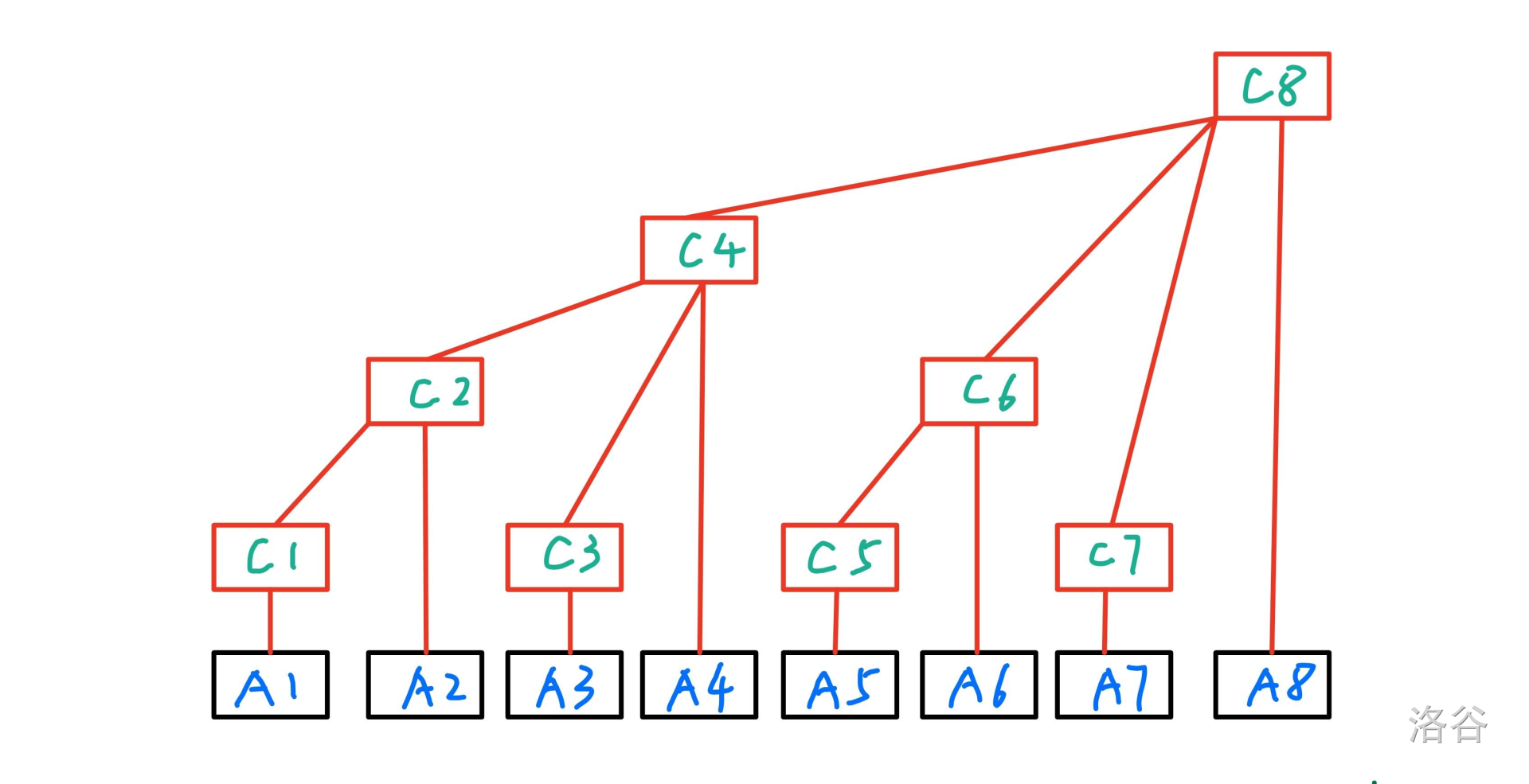
每个点管辖的区域就是最低一位 \(1\) 对应的值(二进制中的,也就是 \(lowbit\),注意,这个地方指的不是位数,而是 \(2^k\)),这个的式子就是这个样子:lowbit(x) = x & -x
然后通过这个就可以简易的计算区间和和区间修改了,复杂度应该是 \(\log n\) 吧)
性质一 :对于 \(x < y\) ,要么有 \(c[x] \in c[y]\) ,要么有 \(c[x] \cap c[y] = \varnothing\)
性质二 :\(c[x] \in c[x + lowbit(x)]\)。
性质三 :对于任意 \(x < y < x + lowbit(x)\),都有 \(c[x] \cap c[y] = \varnothing\)。
可以得出,树状数组抽象化之后其实就是 \(x\) 向 \(x + lowbit(x)\) 连边的一棵树,这棵树天然就包含了很多美好的性质(待补充):
- \(u < fa[u]\)
- \(u\) 大于任何一个它的子代,小于任何一个它的祖先
- 对于任意 \(v < u\) ,如果 \(v\) 不在 \(u\) 的子树上,则 \(c[u] \cap c[v] = \varnothing\)
单点修改的时候其实变动的就是 \(x\) 及 \(x\) 的祖先,所以就是这个样子:
void add(int x,int k){
while(x <= n){
c[x] += k;
x += lowbit(x);
}
}
建树:暴力的话是 \(n\log n\) ,但是其实可以 \(n\) 建边。(其实就是每次算出来一个儿子的值的时候累加到父亲上面去)
区间加区间和:将序列转化为差分序列,然后修改的话就直接单点修改就可以了,然后区间加的话需要推一下式子,这里需要用到两个树状数组,一个存差分数组,还有一个存 \(d_i * i\)(式子待补充)
二维树状数组
也被称为树状数组套树状数组,也就是把序列的操作改到了一个矩阵上面
二维树状数组和一维树状数组类似,在二维树状数组中,\(c[x][y]\) 记录的是右下角为 \((x,y)\),高度为 \(lowbit(x)\) ,宽度为 \(lowbit(y)\) 的区间和
通过这个我们可以推出,当固定一个维度的时候,另一个维度其实就是单纯的一维树状数组,所以修改的时候在原本的一维修改上面增加一个 \(for\)(或者 \(while\))循环就可以了。
区间修改也要推式子,不想推了,于是贴贴:

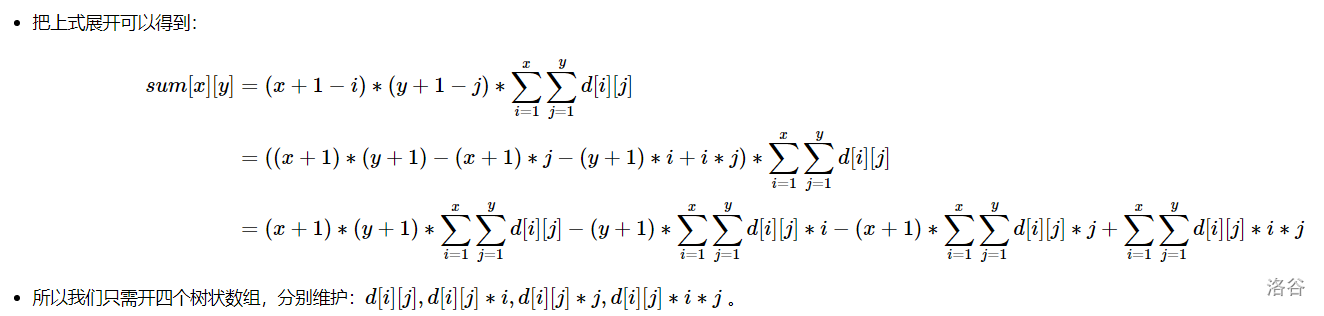
T1 4514 上帝造题的七分钟
就是上面说的二维树状数组区间修改区间查询的板子。结构体好欸。
然后这里数组存的东西和上面说的也差不多。
点击查看代码
int n,m;
struct TREE{
int c[N][N];
int lowbit(int x) {
return x & -x;
}
void add(int x,int y,int val) {
int t = y;
while (x <= n) {
y = t;
while (y <= m) {
c[x][y] += val;
y += lowbit(y);
}
x += lowbit(x);
}
}
int sum(int x,int y) {
int t = y;
int ans = 0;
while (x) {
y = t;
while (y) {
ans += c[x][y];
y -= lowbit(y);
}
x -= lowbit(x);
}
return ans;
}
}c,ci,cj,cij;
void add(int x,int y,int num) {
c.add(x,y,num);
ci.add(x,y,x * num);
cj.add(x,y,y * num);
cij.add(x,y,x * y * num);
}
int sum(int x,int y) {
int ans = 0;
ans += c.sum(x,y) * (x * y + x + y + 1);
ans -= ci.sum(x,y) * (y + 1);
ans -= cj.sum(x,y) * (x + 1);
ans += cij.sum(x,y);
return ans;
}
int main(){
n = fr(),m = fr();
string s;
int a,b,c,d,val;
while (cin >> s) {
a = fr(),b = fr();
c = fr(),d = fr();
if (s[0] == 'L') {
val = fr();
add(c + 1,d + 1,val);
add(a,d + 1,-val);
add(c + 1,b,-val);
add(a,b,val);
} else {
int ans = sum(c,d);
ans += sum(a - 1,b - 1);
ans -= sum(a - 1,d);
ans -= sum(c,b - 1);
fw(ans);
ch;
}
}
return 0;
}
T2 2163 园丁的烦恼
看这个数据范围,就知道单纯的树状数组肯定是不现实的,所以说首先我们要离散化,其次先按照 \(x\) 的坐标给所有询问和树都排一个序(这样后面计算的时候就不需要再考虑 \(x\) 坐标,只需要考虑 \(y\) 坐标了。因为既然已经遍历到了这里,那么前面加入到树状数组里面的树肯定 \(x\) 坐标是小于当前查询的区间的)
按照 \(x\) 排了序之后,把所有 \(y\) 坐标排序再去重(离散化),然后每次查询的话就是查询比当前 \(y\) 坐标小的那个区间的和。
树状数组维护的就是 \(y\) 坐标对应的离散化之后的值所对应的有多少棵树,所以这道题的树状数组是用的单点修改和区间查询,就不用上面那个公式了。
点击查看代码
struct node{
int x,y;
int pos;
bool operator < (const node &t) const{
if (x != t.x) return x < t.x;
if (y != t.y) return y < t.y;
return pos < t.pos;
}
}w[(N << 2) + N];
int n,m,idx;
int tot[N];
int x_1[N],x_2[N],y_1[N],y_2[N];
int ans[N][5];
int h[(N << 2) + N];
int c[(N << 2) + N];
int lowbit(int x) {
return x & -x;
}
void add(int x,int val) {
while (x <= idx) {
c[x] += val;
x += lowbit(x);
}
}
int query(int x) {
int ans = 0;
while (x) {
ans += c[x];
x -= lowbit(x);
}
return ans;
}
int main(){
n = fr(),m = fr();
for (int i = 1; i <= n; i ++) {
int x = fr(),y = fr();
w[++ idx] = {x,y,0};
}
for (int i = 1; i <= m; i ++) {
x_1[i] = fr(),y_1[i] = fr();
x_2[i] = fr(),y_2[i] = fr();
w[++ idx] = {x_1[i] - 1,y_1[i] - 1,i};
w[++ idx] = {x_1[i] - 1,y_2[i],i};
w[++ idx] = {x_2[i],y_1[i] - 1,i};
w[++ idx] = {x_2[i],y_2[i],i};
}
sort(w + 1,w + 1 + idx);
for (int i = 1; i <= idx; i ++)
h[i] = w[i].y;
sort(h + 1,h + 1 + idx);
n = unique(h + 1,h + 1 + idx) - (h + 1);
for (int i = 1; i <= idx; i ++) {
if (w[i].pos) {
int t = lower_bound(h + 1,h + n + 1,w[i].y) - h;
ans[w[i].pos][++ tot[w[i].pos]] = query(t);
} else {
int t = lower_bound(h + 1,h + n + 1,w[i].y) - h;
add(t,1);
}
}
for (int i = 1; i <= m; i ++) {
int res = ans[i][4] - ans[i][3] - ans[i][2] + ans[i][1];
fw(res),ch;
}
return 0;
}
权值树状数组
单点修改,查询全局第 \(k\) 大。
权值树状数组 \(c[i]\) 存储的是给定序列 \(w[i] - w[n]\) 中等于 \(i\) 的元素个数
查询的时候,用倍增代替二分。每次加上 \(2^i\) 的数看看是否超过 \(k\) ,如果是,将 \(i\) 减一,否则将当前位置加上 \(2 ^ i\) ,将 \(k\) 减去对应的个数再继续跳,直到 \(i = 0\) ,答案即为当前位置加一的数。
就感性理解一下吧,实在理解不了就老老实实去弄平衡树的的板子好了。
int kth(int x) {
int pos = 0;
for (int i = 19; i >= 0; i --) {
pos += (1 << i);
if (pos > tot || tr[pos] >= x) {
pos -= (a << i);
} else {
x -= tr[pos];
}
}
return w[pos + 1];
}
(看博客说这个可以解决平衡树解决的问题,不知道是真是假()
树状数组求逆序对
倒序处理原序列,当前数字的前一个数的前缀和即为以该数为较大数的逆序对的个数。例如 \(\{5,4,2,6,3,1\}\) ,倒序处理数字:
- 数字 \(1\) ,\(c[1] ++\),计算 \(c[1]\) 前面的前缀和 \(sum(0) = 0\) ,当前 \(ans = ans + 0 = 0\)
- 数字 \(3\) ,\(c[3] ++\),计算 \(c[3]\) 前面的前缀和 \(sum(2) = 1\) ,当前 \(ans = ans + 1 = 1\)
- 数字 \(6\) ,\(c[6] ++\),计算 \(c[6]\) 前面的前缀和 \(sum(6) = 2\) ,当前 \(ans = ans + 2 = 3\)
......
然后再以此类推求就可以了。
Trie 树
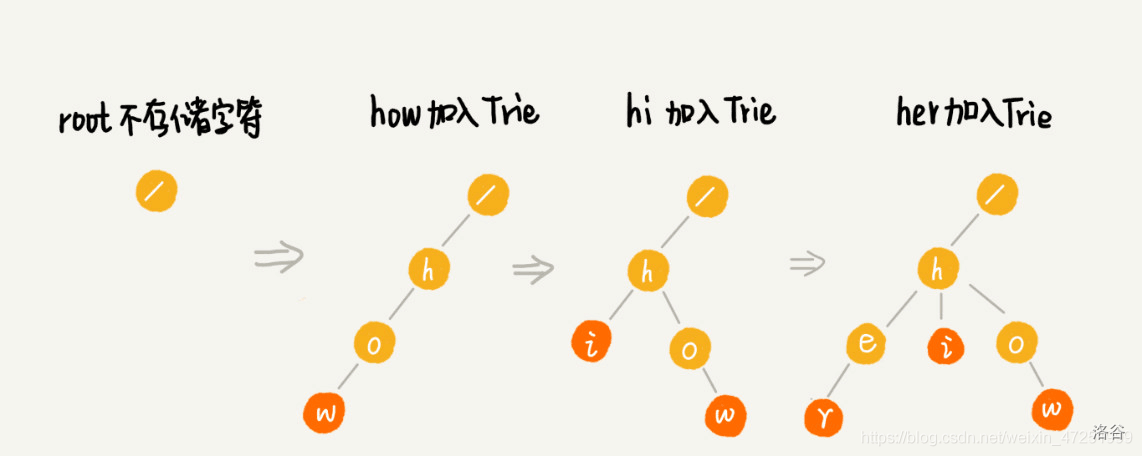
字典树,英文名是 \(Trie\)。最经典的应用就是查询这个单词有没有在之前出现过
构造的话就是这个样子(从别人博客拿的图())
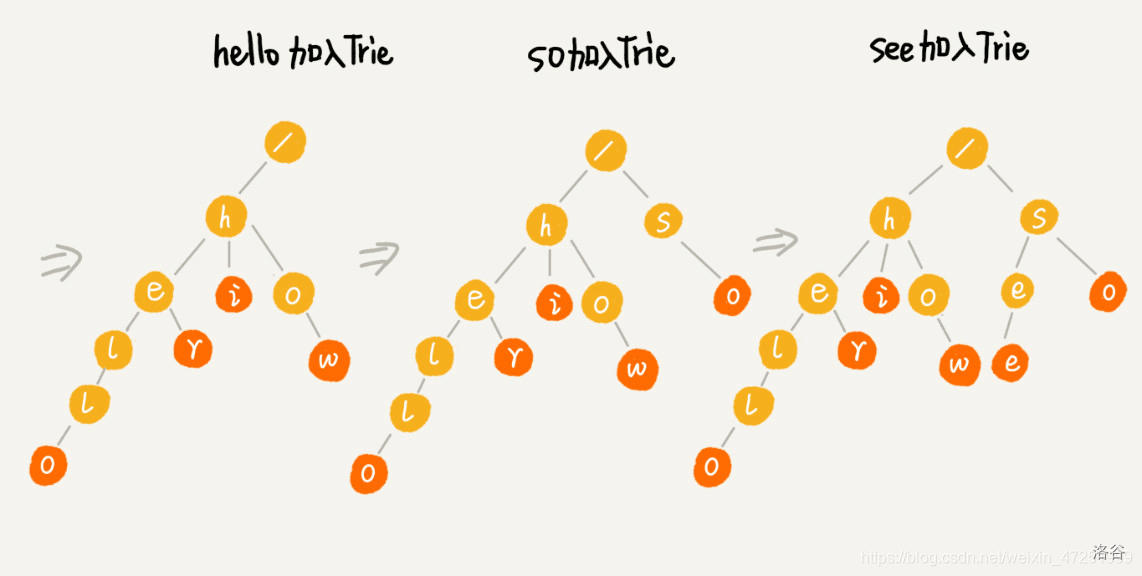
还用来维护异或极值:将数的二进制看做一个字符串,就可以构建出字符集为 \(\{0,1\}\) 的 \(Trie\) 树,求的时候就尽量往不同的位走,就是一个贪心。
练习
今天真是他妈的人麻了,这就是数据结构吗。做的我都不想说话,我的评价是:\(Trie\) 树一生之敌!
A.字典大树
一开始写了个四十分的暴力,但是他们都写的六十分,不知道怎么写的。恼
后来在洛谷上看了题解,发现这道题竟然是从黑题变成蓝题的。\(md\),它难道配不上一个紫吗??
这道题题解做法也多种多样,但是因为我先写的 \(B\) 题用的 \(AC\) 自动机,所以也找了一篇 \(AC\) 自动机的题解看。
建两棵树然后跑 \(AC\) 自动机肯定是扯蛋,所以我们考虑只建一个 \(Trie\) 树该怎么做。我们可以把所有 \(S_i\) 都复制一遍,然后中间加一个间隔符,然后每一个 \(S_i\) 就变成了 \(S_i \& S_i\) ,然后可以观察到中间那一段其实就表示的是后缀加前缀,所以我们对于每一组询问也这样处理,把 \(a_i\) 和 \(b_i\) 拼成这个样子:\(b_i \& a_i\) ,然后就可以跑 \(AC\) 自动机了!
但是这个样子显然是会超时的,那么再优化一下,题解用的是拓扑优化,我也不知道还有没有别的优化,到时候老师讲到 \(AC\) 自动机应该会说的吧。
在一开始 \(insert\) 的时候,就记录一下每个节点结束的字符串的编号,然后建一个 \(fail\) 树,再把这个记录的编号从父节点传到子节点,最后再每一个 \(s_i\) 都跑一遍加一下。
点击查看代码
int n,m,idx;
string s[N],t[N];
int ne[M][6],fail[M];
vector<int> p[M];
vector<int> e[M];
int ans[N];
int f(char c) {
if (c == 'A') return 1;
else if (c == 'U') return 2;
else if (c == 'G') return 3;
else if (c == 'C') return 4;
return 5;
}
void add(int a,int b) {
e[a].push_back(b);
}
void insert(int i) {
int len = t[i].size();
int pos = 0;
for (int j = 0; j < len; j ++) {
int u = f(t[i][j]);
if (!ne[pos][u]) ne[pos][u] = ++ idx;
pos = ne[pos][u];
}
p[pos].push_back(i);
}
void build() {
queue<int> q;
for (int i = 1; i <= 5; i ++) {
if (ne[0][i]) {
q.push(ne[0][i]);
fail[ne[0][i]] = 0;
}
}
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = 1; i <= 5; i ++) {
int pos = ne[u][i];
if (!pos) {
ne[u][i] = ne[fail[u]][i];
} else {
fail[pos] = ne[fail[u]][i];
q.push(pos);
}
}
}
}
void dfs(int u) {
for (auto v : e[u]) {
for (auto x : p[u]) {
p[v].push_back(x);
}
dfs(v);
}
}
void modify(int i) {
int len = s[i].length(),pos = 0;
for (int j = 0; j < len; j ++) {
int u = f(s[i][j]);
pos = ne[pos][u];
for (auto v : p[pos]) {
ans[v] ++;
}
}
}
int main(){
n = fr(),m = fr();
string a,b;
for (int i = 1; i <= n; i ++) {
cin >> a;
s[i] = a + '&' + a;
}
for (int i = 1; i <= m; i ++) {
cin >> a >> b;
t[i] = b + '&' + a;
insert(i);
}
build();
for (int i = 1; i <= idx; i ++)
add(fail[i],i);
dfs(0);
for (int i = 1; i <= n; i ++) {
modify(i);
}
for (int i = 1; i <= m; i ++) {
fw(ans[i]);
ch;
}
return 0;
}
B.树上差分
\(AC\) 自动机 + 树链剖分 + 树状数组。你是会杂糅的。也不长吧,也就 \(200\) 多行而已(?)。
很显然,对字符串进行 \(AC\) 自动机操作之后我们可以通过 \(fail\) 数组建成一棵树。
那么考虑插入一个字符会对哪些字符产生贡献。考虑文本串 \(P\) 匹配的过程:\(P\) 在 \(AC\) 自动机上一个字符一个字符走的过程,相当于枚举了一个前缀,任意时刻在 \(AC\) 自动机(\(Trie\) 图)上走到的节点 \(u\) 代表的字符串,即为该前缀与自动机匹配的最长后缀。那么,我们考虑在 \(u\) 节点这个位置向上跳 \(fail\) 指针,根据 \(fail\) 指针的定义,路径上经过的每一个节点代表的字符串都是 \(P\) 的子串。
注意到根节点是固定的,于是可以考虑将 \(P\) 点在 \(AC\) 自动机上走过的点按照 \(tid\) 的值排一个序(也就是 \(dfs\) 序),然后做下面的事情(假设有 \(k\) 个点):
- 对于每一个 $1 \le i \le k $ ,将 \(u_i\) 在 \(fail\) 树上到根节点上的链的所有答案加一
- 对于每一个 \(1 \le i < k\) ,将 \(LCA(u_i,u_{i + 1})\) 都减去一
这里的 \(LCA\) 可以用树链剖分来加速,然后可以发现这个样子就将问题转化成了:路径加和单点求值。然后我们就可以用树上差分将这个问题再转化为:单点加和子树求和。
这样转化之后,就可以用树状数组解决了。
点击查看代码
#define hx top[x]
#define hy top[y]
int n,Q;
int ne[M][26];
int fail[M],en[N];
int w[M];
char s[M];
int siz[M],fa[M],de[M],son[M],tid[M],rnk[M],top[M],cnt;
vector<int> e[M];
int c[M];
int idx = 1;
void insert(char *s,int id) {
int pos = 1;
int len = strlen(s + 1);
for (int i = 1; i <= len; i ++) {
int u = s[i] - 'a';
if (!ne[pos][u]) ne[pos][u] = ++ idx;
pos = ne[pos][u];
}
en[id] = pos;
}
void build() {
queue<int> q;
for (int i = 0; i < 26; i ++) {
ne[0][i] = 1;
}
q.push(1);
fail[1] = 0;
while (q.size()) {
auto t = q.front();
q.pop();
for (int i = 0; i < 26; i ++) {
int pos = ne[t][i];
if (!pos) {
ne[t][i] = ne[fail[t]][i];
} else {
fail[pos] = ne[fail[t]][i];
q.push(pos);
}
}
}
}
void add_edge(int a,int b) {
e[a].push_back(b);
}
void dfs1(int u,int father) {
de[u] = de[father] + 1;
siz[u] = 1;
fa[u] = father;
for (auto v : e[u]) {
if (v == father) continue;
dfs1(v,u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void dfs2(int u,int st) {
cnt ++;
top[u] = st;
tid[u] = cnt;
rnk[cnt] = u;
if (!son[u]) return ;
dfs2(son[u],st);
for (auto v : e[u]) {
if (v == fa[u] || v == son[u]) continue;
dfs2(v,v);
}
}
int LCA(int x,int y) {
while (hx != hy) {
if (de[hx] < de[hy]) swap(x,y);
x = fa[hx];
}
if (de[x] > de[y]) swap(x,y);
return x;
}
bool cmp(int a,int b) {
return tid[a] < tid[b];
}
int lowbit(int x) {
return x & -x;
}
void add(int x,int val) {
while (x <= idx) {
c[x] += val;
x += lowbit(x);
}
}
int sum(int x) {
int sum = 0;
while (x) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int main(){
n = fr();
for (int i = 1; i <= n; i ++) {
scanf("%s",s + 1);
insert(s,i);
}
Q = fr();
build();
for (int i = 2; i <= idx; i ++) {
add_edge(fail[i],i);
}
dfs1(1,0);
dfs2(1,1);
while (Q --) {
int type = fr();
if (type == 1) {
scanf("%s",s + 1);
int len = strlen(s + 1),pos = 1;
for (int i = 1; i <= len; i ++) {
int u = s[i] - 'a';
pos = ne[pos][u];
w[i] = pos;
}
sort(w + 1,w + 1 + len,cmp);
for (int i = 1; i <= len; i ++) {
pos = w[i];
add(tid[pos],1);
}
for (int i = 1; i < len; i ++) {
pos = w[i];
int q = w[i + 1];
add(tid[LCA(pos,q)],-1);
}
} else {
int i = fr();
int pos = en[i];
int ans = sum(tid[pos] + siz[pos] - 1) - sum(tid[pos] - 1);
fw(ans);
ch;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号