图论

5201 Shortcut G

最短路树，先跑一遍最短路，然后根据跑的最短路来建一个树，我自己写的是在 \(dijkstra\) 里面更新的时候同时更新这个点的父节点，然后最后跑完 \(dijkstra\) 之后再把所有点遍历一遍把树的边给连上。

然后因为一开始有一个点没有过，于是就从题解里面看了一个写法，是跑完最短路之后，再遍历每一条边，如果这条边的权值和 \(dis[ u ]\) 加起来是 \(dis[v]\) 的值的话，就说明当前点是最短路上面的一个点，就标记上。但是由于题解大多都是用的邻接表，所以标记边比较容易，我用vector就建个双向边。还是更喜欢自己的写法。

然后就是需要注意的一点，前面的最短路就是一个小模板，就没什么需要注意的了，但是写 $ dijkstra$ 的时候一定要注意不要一开始就把起点给标记了！！！

还有就是有一个地方我错了好几次，就是题目要求是字典序最小，所以在更新父节点的时候要加一个判断：

else if (dis[v] == dis[u] + w){
	fa[v] = min(fa[v],u);
}

最后一点就是这一题是需要开long long的，我因为懒所以就直接define int long long了，所以可能要慢一点（）

然后 核心代码

if (dis[v] > dis[u] + w){
	dis[v] = dis[u] + w;
	fa[v] = u;
	q.push({v,dis[v]});
}
else if (dis[v] == dis[u] + w){
	fa[v] = min(fa[v],u);
}

void dfs(int u){
	for(auto v:ez[u]){
		dfs(v);
		a[u] += a[v];
	}
	ans = max(ans,(dis[u] - t)*a[u]);
}

for (int u = 1; u <= n; u ++){
		ez[fa[u]].push_back(u);
	}

货车运输

是一道杂糅题吧算，可惜了没有最短路。是最大生成树（和最小生成树的写法极其类似，就是把小于号改成大于号），然后用 $ vector $ 存边，接着再跑一遍 $ LCA $ 就可以啦。

然后 $ minn $ 更新的话就和 $ fa $ 数组同时更新就可以了。最后再跑一遍 $ LCA $ ，找最近公共祖先的同时更新 $ ans $ 。

注意点

1. $ LCA $ 里面的左移和右移符号不要写反了！！！
2. 在更新 $ minn $ 的时候，要注意是当前 $ u $ 的 $ k - 1 $ 和当前 $ u $ 的 $ k - 1 $ 的父亲的 $ k - 1 $ ，不是自己和自己的 $ k - 1 $ 。
3. 在 $ LCA $ 里面更新 $ ans $ 的时候，要先更新再改变 $ x $ 和 $ y $ 的值，不然 $ ans $ 更新的就是一个错的
4. 在找到最近公共祖先的时候，普通 $ LCA $ 是返回这个点的最近父亲，而这一个是再次更新 $ ans $ 的值

核心代码

void init(int u,int p,int ww){
	de[u] = de[p] + 1;
	fa[u][0] = p;
	minn[u][0] = ww;
	for (int k = 1; (1<<k) <= de[u]; k ++){
		fa[u][k] = fa[fa[u][k - 1]][k - 1];
		minn[u][k] = min(minn[u][k-1],minn[fa[u][k - 1]][k - 1]);
	}
	for (auto &it : e[u]){
		int v = it.v,w = it.w;
		if (v == p) continue;
		init(v,u,w);
	}
}

int LCA(int x,int y){
	if (de[x] < de[y])
		swap(x,y);
	
	int ans = inf;
	int dh = de[x] - de[y];
	int kmax = log2(dh);
	for (int k = kmax; k >= 0; k --){
		if (dh & (1 << k)){
			ans = min(ans,minn[x][k]);
			x = fa[x][k];
		}
	}
	
	if (x == y) return ans;
	
	kmax = log2(de[x]);
	for (int k = kmax; k >= 0; k --){
		if (fa[y][k] != fa[x][k]){
			ans = min(ans,minn[y][k]);
			ans = min(ans,minn[x][k]);
			x = fa[x][k];
			y = fa[y][k];
		}
	}
	
	ans = min(ans,minn[x][0]);
	ans = min(ans,minn[y][0]);
	
	return ans;
}


sort(edge + 1,edge + 1 + m);
for (int i = 1; i <= m; i ++){
	int ha = find(edge[i].a);
	int hb = find(edge[i].b);
	if (ha != hb){
		a = edge[i].a,b = edge[i].b;
		h[ha] = hb;
		e[a].push_back({b,edge[i].w});
		e[b].push_back({a,edge[i].w});
	}
}

2754 飞行员配对问题

是一道网络流的题目，算是做的第一道网络流的不是模板的题目。然后网络流的 $ dinic $ 在这里。

主要是建边方法捏，这一题其实是二分图，但是学了网络流谁还用匈牙利哦。建边的话建立一个虚拟源点和虚拟汇点（算是吧），然后把所有一边的点向源点连一条边，把另一边的点向汇点连一条边（这道题的边权都是1）。后面说每一对的时候，就在这两条边之间连一条边。

然后就没什么了（），代码

S = 0,T = n + 1;
memset(h,-1,sizeof h);
for (int i = 1; i <= m; i ++) {
	add(S,i,1);
}
for (int i = m + 1; i <= n; i ++) {
	add(i,T,1);
}
int a,b;
while (1) {
	a = fr(), b = fr();
	if (a == -1) break;
	add(a,b,1);
}

int ans = dinic();
fw(ans);
ch;
for (int i = 0; i < idx; i += 2) {
	if (e[i] > m && e[i] <= n && !f[i]) {
		fw(e[i ^ 1]),kg,fw(e[i]);
		ch;
	}
}

4843 清理雪道

也是一道网络流的题，比较水，但是一开始还是调了好久，主要是 $ dinic $ 板子打错了，也不是打错了，就是在 $ bfs $ 的时候没有一开始把 $ S $ 点加进去，然后 $ h $ 一开始又没有初始化为 $ -1 $ 。

建图：

1. 首先发现这一题是上下界无源汇的最小流（？），于是想着把他转化为有源汇的，然后转成有源汇之后发现他是多源汇的，所以再建一个源点和汇点。

2. 每一个点都和 $ t $ 还有 $ s $ 连一条没有没有下界的容量上界为 $ inf $ 的边（应该就是没有上下界），然后每一个边连一条上界为 $ inf $ 下界为 $ 1 $ 的边，然后后面就是有源汇最小流的板子

S = 0,T = n + 3;
s = n + 1,t = n + 2;
for (int i = 1; i <= n; i ++) {
	m = fr();
	add(s,i,inf);
	add(i,t,inf);
	while (m --) {
		int a = fr();
		add(i,a,inf - 1);
		d[a] ++,d[i] --;
	}
}
for (int i = 1; i <= n; i ++) {
	if (d[i] > 0) add(S,i,d[i]);
	else if (d[i] < 0) add(i,T,- d[i]);
}
int ans = dinic();
add(t,s,inf);
ans = dinic();

2764 最小路径覆盖

建图：先把每个点拆成出点和入点，然后把每一个出点和虚拟源点 $ S $ 连一条边，然后每一个入点和虚拟汇点 $ T $ 连一条边。原图中的边就是出点到入点连一条边就可以了。因为题目中说了不能交叉，也就是说每一个点都只能用一次，所以说这里的容量统一设置为 $ 1 $

贴个图，这里面的黑色边是原图中的边，然后图中每一条边的边权都是 $ 1 $

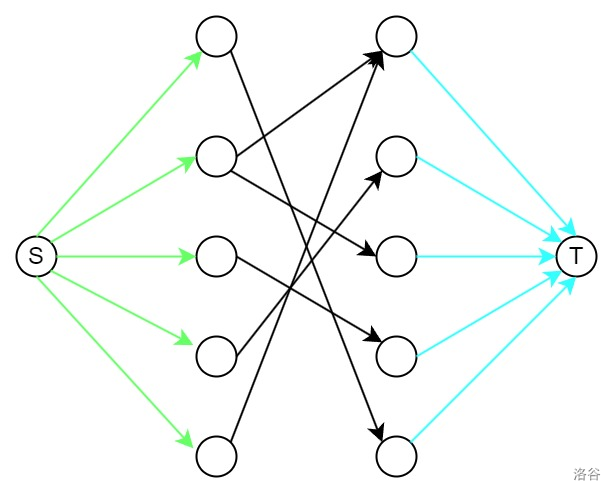
这样子建图之后跑出来的最大流就是二分图的最大匹配数（最小点覆盖）。显而易见题目要求求的最小路径覆盖就是总的点数减去最大匹配数。

然后求路径的时候，用并查集把每一条路径上面的点给存起来，然后再 $ dfs $ 跑一遍就可以了。然后因为这里拆点了，所以说要 $ -n $ 。

在 $ for $ 循环里面的条件就是说这个边的起点要是一个出点，终点要是一个入点，然后他们之间在残留网络中流量为 $ 0 $ ，也就是说这两个点是相连的。

还有要注意的是，因为这里的函数比较多，有 $ dinic $ 的 $ dfs $ ，有并查集的 $ find $ ，还有一个求路径的 $ get $ ，所以函数名不要搞混了。与之相同的还有就是不要把并查集的 $ fa[i] $ 和领接表 $ h[i] $ 的搞混了捏。

贴个路径和建边（）

void get(int u,int head) {
	fw(u),kg;
	flag[u] = true;
	for (int i = h[u]; ~ i; i = ne[i]) {
		int v = e[i] - n;
		if (!flag[v] && fa[v] == head)
			get(v,head);
	}
}

for (int i = 1; i <= n; i ++) {
	add(S,i,1);//green
	add(i + n,T,1);//blue
}
while (m --) {
	a = fr(), b = fr();
	add(a,b + n,1);//black
}
int ans = n - dinic();
for (int i = 1; i <= n; i ++) {
	fa[i] = i;
}
for (int i = 0; i < idx; i += 2) {
	a = e[i ^ 1],b = e[i];
	if (a > 0 && a <= n && b > n && b <= 2 * n && !f[i]) {
		b -= n;//******还原//
		int ha = find(a),hb = find(b);
		if (ha != hb) fa[hb] = ha;
	}
}
for (int i = 1; i <= n; i ++) {
	if (fa[i] == i) {
		get(i,i);
		ch;
	}
}