PCA与KPCA
PCA是利用特征的协方差矩阵判断变量间的方差一致性,寻找出变量之间的最佳的线性组合,来代替特征,从而达到降维的目的,但从其定义和计算方式中就可以看出,这是一种线性降维的方法,如果特征之间的关系是非线性的,用线性关系去刻画他们就会显得低效,KPCA正是应此而生,KPCA利用核化的思想,将样本的空间映射到更高维度的空间,再利用这个更高的维度空间进行线性降维。
如果样本的维度是k,样本个数是n(n>k),那么首先需要将样本投射到n维空间,这个n维空间是这样计算的:首先计算n个样本间的距离矩阵D(n*n),核函数F,则F(D)就是他的高维空间投射。
我们用几个例子来看KPCA与PCA的不同:我们用三维空间中三个同心球面来作为三类原始数据,用不同的核函数来将其降维到二维平面,当核函数是linear(线性)时,就是PCA,其他的核函数,如RBF,SIGMOID,多项式等,都是非常常用的核化函数。
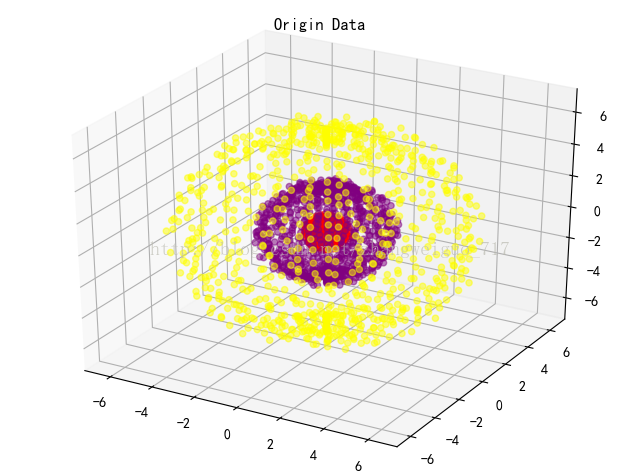
原始数据分布点如下,共2700个样本,每一类样本900个:
用KPCA各类核函数将其降维后,达到效果如下:
很明显,RBF核能将不同类别的数据分开,而PCA只是将其做了一个投影,在这里,由于三个球是相互嵌套的,很难找到合适的投影方向,将三类数据很好的分开,由此造成了非常差的表现,KPCA的优点由此可见。
作者:jsp
-------------------------------------------
个性签名:无论在哪里做什么,只要坚持服务、创新、创造价值,其它的东西自然都会来的。
如果觉得这篇文章对你有小小的帮助的话,记得在右下角点个“推荐”哦,博主在此感谢!





 浙公网安备 33010602011771号
浙公网安备 33010602011771号