密度泛函理论发展简史1

密度泛函理论发展简史（一）

现如今，理论计算物理变得越来越重要。它的发展，使得我们可以加快新材料的研发进程。在刚开始学习阶段，我也一直把它当作一种“黑箱”在使用：拿到软件后，仅进行简单的参数调整，却并不理解其内在的物理机理。经过一学期的学习，从多体系统出发，逐步简化，最终到达了我们所熟知的、可实际求解的模型——如平面波方法、原子轨道方法等。这一过程也清晰地体现了物理学中对复杂问题“不断简化、不断粗糙化”的处理思路。

多体系统

从最基本的定态薛定谔方程出发：

\[\hat{H} \Psi = E \Psi \]

其中，波函数 \(\Psi\) 同时依赖于原子核坐标 \(\mathbf{R}\) 和电子坐标 \(\mathbf{r}\)；\(E\) 为多体系统的总能量；哈密顿算符 \(\hat{H}\) 包含以下五个部分：

• 原子核动能 \(\hat{T}_n\)
• 电子动能 \(\hat{T}_e\)
• 原子核–原子核相互作用 \(\hat{U}_{nn}\)
• 电子–电子相互作用 \(\hat{U}_{ee}\)
• 原子核–电子相互作用 \(\hat{U}_{ne}\)

即：

\[\hat{H} = \hat{T}_n + \hat{T}_e + \hat{U}_{nn} + \hat{U}_{ee} + \hat{U}_{ne} \]

在原子单位制下，这五项可以明确写出：

• 原子核动能：

  \[\hat{T}_n = \sum_a -\frac{1}{2M_a} \nabla_a^2 \]

• 电子动能：

  \[\hat{T}_e = \sum_i -\frac{1}{2} \nabla_i^2 \]

• 相互作用项均为库仑作用，形式为：

  \[\hat{U}_{nn} = \sum_{a < b} \frac{Z_a Z_b}{|\mathbf{R}_a - \mathbf{R}_b|}, \quad \hat{U}_{ne} = -\sum_{a,i} \frac{Z_a}{|\mathbf{R}_a - \mathbf{r}_i|}, \quad \hat{U}_{ee} = \sum_{i < j} \frac{1}{|\mathbf{r}_i - \mathbf{r}_j|} \]

思考

我们会发现：尽管多电子体系的哈密顿量可以精确写出，但电子与原子核之间高度耦合，导致直接求解极其困难。以一个简单的水分子（H₂O）为例：包含3个原子核和10个电子。仅考虑两两相互作用项，通过排列组合即可得出多达78项。而两个水分子组成的体系，其复杂度并非简单翻倍，而是呈指数级增长。因此，我们必须对问题进行简化、再简化，才能使其在计算上可行。

---

附录：原子单位制

原子单位制（Atomic Units, a.u.）是一种在量子化学和凝聚态物理中广泛使用的自然单位系统。其核心思想是将若干基本物理常数归一化为1，从而简化公式表达。

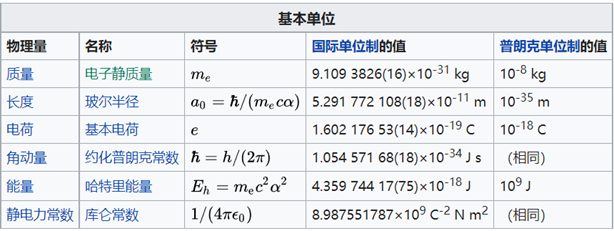
常用的六个基本量包括：

• 电子质量 \(m_e\)
• 基本电荷 \(e\)
• 约化普朗克常数 \(\hbar\)
• 库仑常数 \(\frac{1}{4\pi\varepsilon_0}\)
• 哈特里能量 \(E_h\)
• 玻尔半径 \(a_0\)

这六个量并非相互独立。实际上，只需将其中任意四个设为1，其余两个便会自动归一化。

更详细内容可参考：
中文维基百科：原子单位制
英文维基百科：Hartree atomic units