【转载】极大值与等高线

 

https://blog.csdn.net/quicmous/article/details/52527507

最优化问题

　　数学规划问题，或着说最优化问题，一般可写成下面的形式：

 

maxs.t.f(x)g(x)=c(1)(1)

maxf(x)s.t.g(x)=c

 

先看看二维的问题

　　为了简单起见，我们考虑二维情况，假设x=(x1,x2)x=(x1,x2) ，则最优化问题变成如下形式：

 

maxs.t.f(x1,x2)g(x1,x2)=c(2)(2)maxf(x1,x2)s.t.g(x1,x2)=c

 

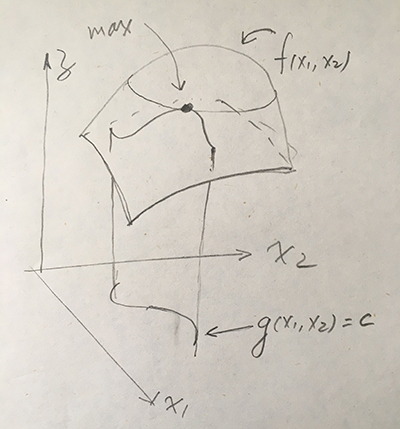
　　几何意义非常明显，要求在曲线 g(x1,x2)=cg(x1,x2)=c 上找一点，使得函数 f(x1,x2)f(x1,x2) 取得最大值。因为f(x1,x2)f(x1,x2) 是一个曲面，形象一点说，问题就是在山上寻找一条山路的最高点。

聊一聊等高线

　　求解最优规划问题的关键在于曲面的等高线。我们停下脚步，看看等高线有趣的性质。对于曲面f(x1,x2)f(x1,x2) 来说，其等高线可以表示成下面的形式，

 

f(x1,x2)=c(3)(3)f(x1,x2)=c

　　两边进行微分，得到，

 

∂f∂x1dx1+∂f∂x2dx2=0(4)(4)∂f∂x1dx1+∂f∂x2dx2=0

　　可以看出，dx1,dx2dx1,dx2 之间是有关系的。实际上，微分dx=(dx1,dx2)dx=(dx1,dx2) 与曲线f(x1,x2)=cf(x1,x2)=c 切线方向一致。如果觉得不好理解的话，可以吧x1,x2x1,x2 换成x,yx,y ，问题就变成一元函数求导，我们知道dy/dxdy/dx 表示曲线的切线斜率，当然(dx,dy)(dx,dy) 就与曲线的切线方向相同。于是，我们得到曲面等高线的切线向量，

 

dx=(dx1,dx2)(5)(5)dx=(dx1,dx2)

　　我们知道，曲面f(x1,x2)f(x1,x2) 的梯度可表示为，

 

∇f(x1,x2)=(∂f∂x1,∂f∂x2)(6)(6)∇f(x1,x2)=(∂f∂x1,∂f∂x2)

　　于是(4)式可以表示为，

 

∇f⋅dx=0(7)(7)∇f⋅dx=0

　　可以看出，曲面上任意一点，其等高线的切线方向与其梯度方向相互垂直。

 

约束条件本质上是曲面的等高线

　　约束条件g(x1,x2)=cg(x1,x2)=c ，实际上就是曲面g(x1,x2)g(x1,x2) 的一条等高线。根据前面的结论，它的切线方向与梯度方向垂直。

目标函数的等高线

　　二元函数的最优规划问题，和寻找山间小路上的最高点的思路是一样。到达山间小路最高点位置后，无论沿山间小路哪个方向走，都是下坡，都会走向较低的等高线，因此，在小路的最高点位置，小路必须与山坡的等高线相切。
　　同样，我们沿着曲线 g(x1,x2)=cg(x1,x2)=c 到达最曲面f(x1,x2)f(x1,x2) 最高点，这条小路一定与曲面 f(x1,x2)f(x1,x2) 在此位置的等高线相切，也就是曲线 g(x1,x2)=cg(x1,x2)=c 与曲线 f(x1,x2)=c′f(x1,x2)=c′ 在最大值位置相切。或者从梯度的角度来看，曲面f(x1,x2),g(x1,x2)f(x1,x2),g(x1,x2) 在最大值位置梯度方向是相同的。
　　换句话讲，如果规划问题在(x1,x2)(x1,x2) 处取得最大值，一定存在常数 λλ 使得，

 

∇f(x1,x2)=λ∇g(x1,x2)(8)(8)∇f(x1,x2)=λ∇g(x1,x2)

　　看到这里怎么有些懵圈呢？最优解和常数 cc 怎么就没关系了呢？不是说好的 g(x1,x2)=cg(x1,x2)=c 吗？实际上， λλ 是待定参数， cc 的值可以用来确定 λλ 的值。下面我们牛刀小试，看一个具体的例子。

 

一个具体例子

　　例1 求下面规划，

 

maxs.t.10−(x1−1)2+(x2−2)22x1+x2=1(9)(9)max10−(x1−1)2+(x2−2)2s.t.2x1+x2=1

　　解：

 

f(x1,x2)g(x1,x2)==10−(x1−1)2+(x2−2)22x1+x2f(x1,x2)=10−(x1−1)2+(x2−2)2g(x1,x2)=2x1+x2

　　由于，

 

∇f(x1,x2)=λ∇g(x1,x2)∇f(x1,x2)=λ∇g(x1,x2)

　　于是，

 

(−2x1+2,−2x2+4)=λ(2,1)(−2x1+2,−2x2+4)=λ(2,1)

　　即，

 

{−2x1+2−2x2+4==2λλ{−2x1+2=2λ−2x2+4=λ

　　所以，

 

x1=−λ+1,x2=−12λ+2(10)(10)x1=−λ+1,x2=−12λ+2

　　代入(9)，

 

2x1+x2=12x1+x2=1

　　即，

 

λ=65λ=65

　　代入(10)，得，

 

x1=−15,x2=75x1=−15,x2=75

　　此时，

 

f(x1,x2)===10−(x1−1)2+(x2−2)210−(−15−1)2+(75−2)2......f(x1,x2)=10−(x1−1)2+(x2−2)2=10−(−15−1)2+(75−2)2=.