链接:https://www.zhihu.com/question/36714044/answer/78680948
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
稍微系统的讲讲 Logistic 方程在生态学上的出现背景,意义和应用场景。
1.来源
1798年的时候一个叫 Malthus 的英国牧师在查看当地的人口出生记录的时候发现人口的变化率是和人口的数目成正比的,当然你也可以认为这个正比的关系是生态学上的一个基本假设。
如果用这个函数来表示
时刻某个地区的人口总数(或者是牛羊的数目或者是细菌的数目)的话我们得到的应该是下面这个方程:
其中是常数,表示
的变化率。(注意这里为了方便我直接写了连续极限下的方程并且忽略掉了一些随机效应的影响,理论上讲只有系统尺寸趋于无穷大的情况下这个描述才是准确的,但这样写并不影响我们理解问题的本质。下面用了同样的处理。)
这个微分方程可以直接积分解出:
其中是积分常数,不过这里可以理解为系统的初值即
。如果考虑
的情况下显然
会随着时间指数增长(如下图),如果自然界确实是按照这个规律工作的那么地球早该被各种生物塞的满满的。另一方面如果
那么
就会指数衰减,这部分就不细说了,后面主要还是关注种群增长的问题。
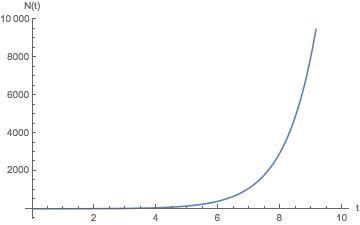
图1:随时间指数增长
为了克服数目无限增长的问题,模型必须做出修改才行,这个修改最早由 Pierre-François Verhulst 在1838年提出:
这就是所谓的 Logistic 方程了。能看出是在原有模型的基础上增加了这一项。
也是个常数,用来表示系统的容量(capacity),这里认为不管是什么物种生存环境总是有限制的,这个限制可以体现在空间或者资源上。
多了这一项最直接的结果就是系统不能无限制的增长了:随着随时间的增长并不断接近系统的容量
,
的增长率是逐渐减小的。后面我们会更详细的考察这个方程的性质,这里先直观的看看模型设计成这样的意义。
Logistic 方程描述的系统中人口的增长率除了和当时的人口数目成正比以外还要受到系统容量的限制;或者你可以理解为人口的增长速度除了和当时的人口数目成正比以外还和系统中的空位成正比。
为了下面讨论方便,我们先把 Logistic 方程重新标度一下,令:
并在方程两边同时除以,方程变为:
这是 Logistic 方程更一般的形式,这里表示人口在容量确定的系统中所占的比例。
2. Logistic 方程的性质
实际上 Logistic 方程是可以直接解出的:
为了更直观的考察方程的性质,现在我们假设初始时刻的取值是多种多样的,我们关心的是随着时间的流逝,
是如何变化的,看图:
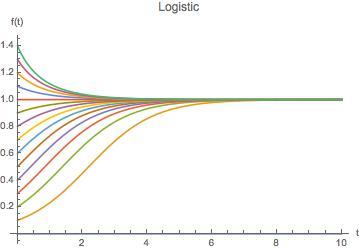
图2:分别取
区间上一些不同的值的情况下
随时间的变化情况
从图中可以看到很多有意思的东西:
最明显的,不管初值如何取,最终都会变到
!无限制增长的问题被解决了。
细心的朋友应该发现图中有些是大于1的,如果要求一个萝卜一个坑的话这当然是不可能的,但如果系统容量的限制没有那么强允许大家都挤一挤的话这种情况还是可以理解的。有意思的尽管初值大于
,
还是很快就变到1了,完全符合逻辑。这么一看 Logistic 方程虽然简单但实在很巧妙。
另外图中还有一条的线因为和横轴重叠了所以看不清,这条线也好理解,如果一开始
那么
就永远等于
。
下面这段话只作为辅助理解。 有朋友应该已经意识到了对 Logistic 方程来说,和
是两个很特殊的点,当
取到这两个点的时候方程的右边为0也即
的变化率为0。我们称这两个点为不动点。但这两个点又不一样,其中1是稳定不动点,0是不稳定的,形象一点的理解的话0点在山的最高峰,1在最谷底,如果你恰巧落在了0点,那么可以保持不动,除此之外落在其他的任何
上的地方都会最终跑到1处去。因为现实世界并非是确定性的,所以不太容易见到系统保持在0这样的不稳定不动点上,相比之下1因为其稳定性要常见的多。 这里并没有讨论
的情况,因为在生态学上这是没有意义的,不过感兴趣的朋友可以自己分析一下会是个什么情况。
3.应用
3.1 生态学上的应用
因为 Logistic 方程形式简单但内涵丰富所以本身就是个很好的模型,到现在也常常被拿出来说明问题。
有时也在其基础上做一些改动来描述更加复杂的情况。比如下面这个方程:
多出来的这个也是个常数,叫做 Allee 阈值,比较有趣的是
的情况,看图:
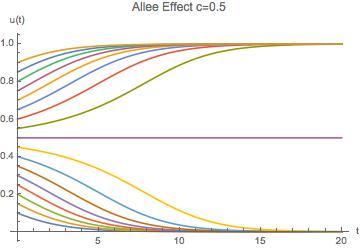
图3: 的情况下不同初值随时间变化的情况
多了这一项以后方程的不动点变成三个,稳定性也有所变化。直接从图上看的话就是如果
,
最后会趋于1;如果
,
最后会趋于0。
这描述了这样一个情景:如果在一个新的环境下群体的数目不是足够多到超过了某个阈值,那么这个群体会最终消亡;如果达到了这个阈值,则可以兴盛繁荣。这个作用被称为 Allee 效应,体现了群体里面个体之间相互依存的关系。
3.2 在化学上的应用
考虑下面这个化学反应:
速率为
速率为
假设系统中总的粒子数是确定的用分别表示两种物质的浓度,并考虑
会得到下面的方程:
得到的也是个类 Logistic 形式的方程。这至少说明 Logistic 方程的形式有很强的普遍性。
其他方面的应用可以参考其他的答案,我不太懂就不多说了。
4.彩蛋
Logistic 方程其实远不是表面上看起来的这么简单。考虑它的分立形式:
这就是大名鼎鼎的 Logistic 映射了,迭代这个映射会出现混沌!

图4: Logistic 映射的分岔图
5.参考文献
对系统生物学感兴趣的朋友可以看看这本:《Mathematical Biology (豆瓣)》 对数学要求会高一点。
Logistic 方程是个简单的非线性动力系统,简单的分析可以参考《常微分方程 (豆瓣)》
如果你还对混沌感兴趣的话那么看这本:《Differential Equations, Dynamical Systems, and an Introduction to Chaos, Third Edition (豆瓣)》才发现这书已经出到第三版了



 浙公网安备 33010602011771号
浙公网安备 33010602011771号