前缀和与差分
前缀和与差分
1. 一维前缀和
在学习前缀和之前,我们先来看一个题目,了解前缀和的用处。
链接: 题目链接
题目描述
给定一个数组a,有q次询问,对于每次询问:给定两个数 l,r。求第l个数到第r个数的和。
输入描述
第一行一个整数表示样例个数T,1<=T<=10 。
对于每组样例:
第一行两个整数n,q, 分别表示数组长度和询问次数。1<=n,q<=1e5.
第二行n个整数,表示数组a,-1e9<=ai<=1e9.
接下来q行,每行两个整数l,r 表示询问的区间。
输出描述
对于每组样例,一行一个整数表示答案。
输入样例
2
5 3
1 2 3 4 5
1 2
2 5
3 4
7 2
-1 9 -10 8 2 6 11
1 5
2 7
输出样例
3
14
7
8
26
暴力解法:
对于每一次询问,遍历区间进行求和,时间复杂度为O(T* n*q),最大为1e11,所以暴力必然超时。
改变思路,用前缀和,对于每一次询问都可以通过O(1)的复杂度实现。
实现方法:再开一个数组pre,用来保存a数组的前 i 项和。
即:pre[i]=pre[i-1]+a[i];
要求 l - r 区间的和即求 : pre[r]-pre[l-1];

话不多说,上代码
一维前缀和
//2024 jin
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N], pre[N];//记得开ll ,int会爆
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
{
int n, q;
cin >> n >> q;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
//前缀和
pre[i] = pre[i - 1] + a[i];
}
while (q--)
{
int l, r;
cin >> l >> r;
cout << pre[r] - pre[l - 1] << '\n';
}
}
return 0;
}
2.一维差分
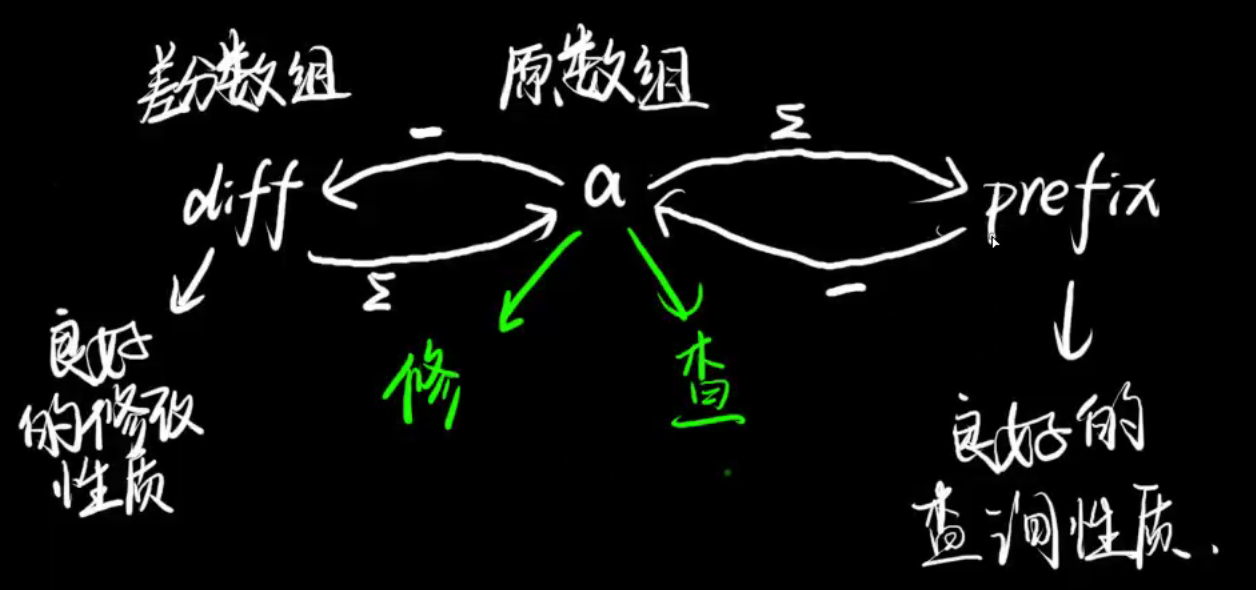
首先来介绍一下差分数组(diff),diff[i]=a[i]-a[i-1],差分与前缀和的区别就是一个是减,一个是加。
由上面一维前缀和我们了解到前缀和可以快速求出一个区间的和。接下来我们看看差分有哪些妙用。
1.还原成a[i]:对差分数组进行前缀和能还原出a[i]。
2.区间修改:差分数组能够快速的对区间进行修改,时间复杂度为O(1)。


接下来看一个题目
链接: 题目链接
题目描述
给定一个长度为n的数组a,和两个整数p,q。
先进行p次区间加操作:将区间[l,r]的数字都加上x。
再进行q次区间查询操作:求出[l,r]的数字之和。
对于每次区间查询操作,输出结果。
输入描述
第一行三个整数𝑛,𝑝,𝑞(1≤𝑛≤1e5,0≤𝑝≤1e5,0≤q≤1e5)(1≤n≤1e5)
第二行𝑛个整数表示数组𝑎。(−1e9≤𝑎𝑖≤1e9)
接下来𝑝行,每行三个整数𝑙,𝑟,𝑥。(1≤𝑙≤𝑟≤𝑛,−1e9≤𝑥≤1e9)
接下来𝑞行,每行两个整数𝑙,𝑟。(1≤𝑙≤𝑟≤𝑛)
输出描述
对于每次区间查询操作,输出结果。
输入样例
5 1 2
1 1 1 2 2
1 4 2
1 3
1 5
输出样例
9
15
结合前面的分析,我们先通过差分数组完成p次对区间的修改,在对其进行前缀和处理还原 a 数组,再对 a 数组进行前缀和,即可完成 q 次区间和的询问。
OK,思路没问题,上代码。
一维差分。
//2024 jin
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N], pre[N], diff[N];//开ll ,int会爆
void solve()
{
int n, p, q;
cin >> n >> p >> q;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
//差分
diff[i] = a[i] - a[i - 1];
}
while (p--)
{
int l, r, x;
cin >> l >> r >> x;
//区间修改
diff[l] += x;
diff[r + 1] -= x;
}
for (int i = 1; i <= n; i++)
{
//前缀和还原a数组
a[i] = a[i - 1] + diff[i];
//对a进行前缀和
pre[i] = a[i] + pre[i - 1];
}
while (q--)
{
int l, r;
cin >> l >> r;
cout << pre[r] - pre[l - 1] << '\n';
}
return;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}
3.二维前缀和
我们直接来介绍二维前缀和吧。
在二维前缀和中,pre[i][j]表示从[ 1,1 ]到[ i , j ] 的矩形中所有元素的和。

那我们要怎么计算这个前缀和数组呢?

辅助理解
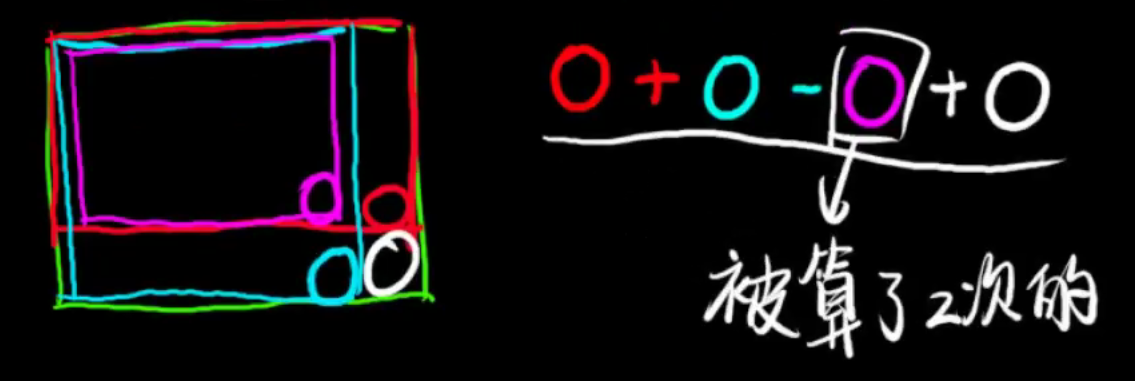
好了我们再来看一个例题
链接: 题目链接
题目描述
给定一个𝑛行𝑚m列的整数矩阵。
有𝑞个询问,每个询问格式为:𝑥1,𝑦1,𝑥2,𝑦2 ,表示一个子矩阵的左上角和右下角的坐标。
对于每个询问,请回答子矩阵的所有数之和。
输入描述
第一行包括三个整数𝑛,𝑚,𝑞(1≤𝑛,𝑚≤1e3,1≤𝑞≤1e5)
接下来𝑛行,每行包括𝑚个整数,表示整数矩阵(每个整数的取值范围为[1,1e5])。
接下来𝑞行,每行包括四个整数𝑥1,𝑦1,𝑥2,𝑦2 (1≤𝑥1≤𝑥2≤𝑛,1≤𝑦1≤𝑦2≤𝑚),表示一个询问的左上角、右下角坐标。
输出描述
共𝑞行,第𝑖(1≤𝑖≤𝑞)行输出第𝑖个询问的结果。
输入样例
7 3 2
3 5 1
6 2 4
7 9 10
4 3 6
3 9 9
6 10 1
9 10 4
2 2 7 3
2 1 4 2
输出样例
77
31
这里我就不说暴力做法了,肯定会超时的。
直接上我们的二维前缀和。
前面已经讲了如何来计算二维前缀和数组了,接下来就是如何通过二维前缀和数组来查询 [x1,y1] 到 [x2,y2] 的区间和了。
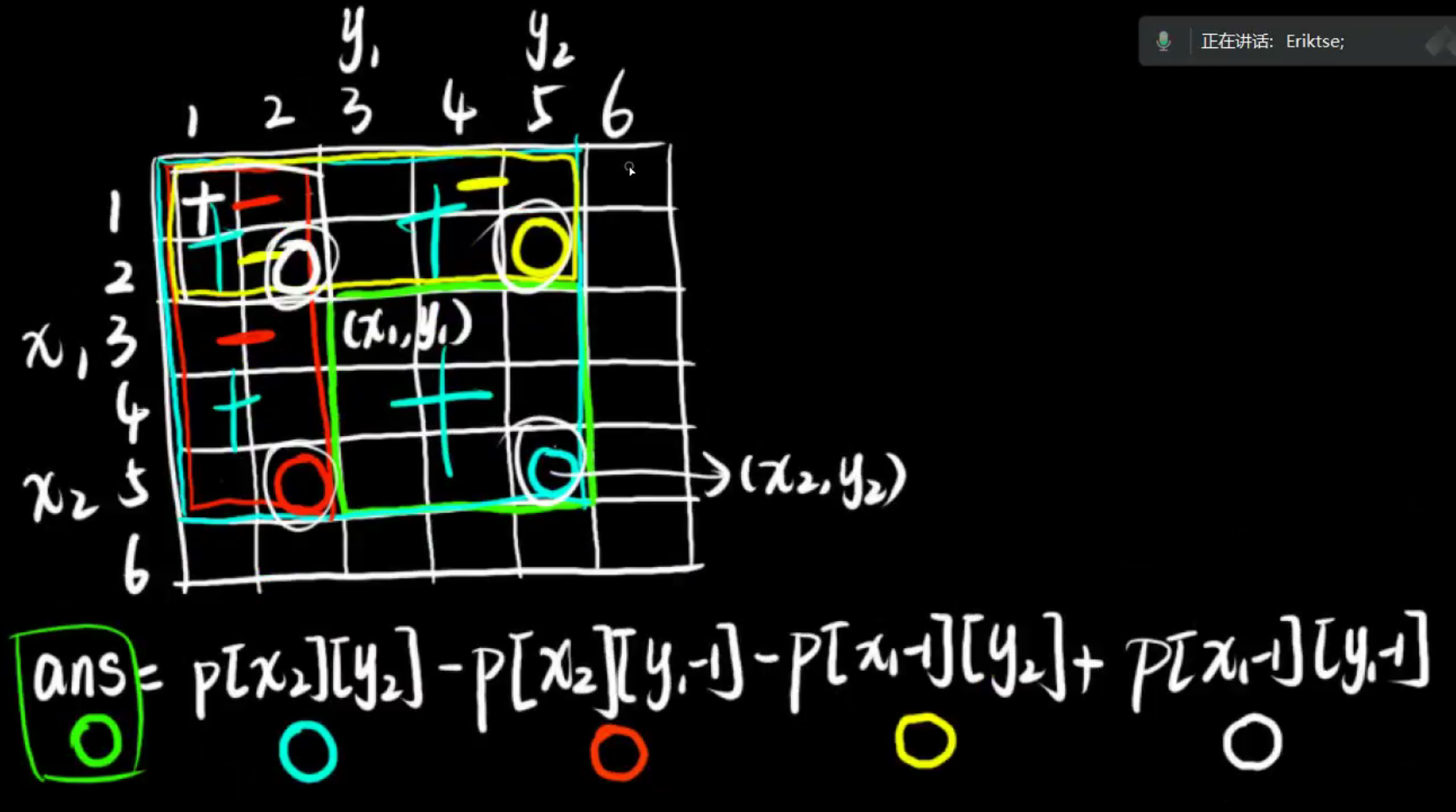
一切准备就绪,上代码
二维前缀和
//2024 jin
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 9;
ll a[N][N], pre[N][N];//开ll
void solve()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
//计算二维前缀和
pre[i][j] = pre[i][j - 1] + pre[i - 1][j] - pre[i - 1][j - 1] + a[i][j];
}
}
while (q--)
{
int x1, x2, y1, y2;
cin >> x1 >> y1 >> x2 >> y2;
//查询操作
ll ans = pre[x2][y2] - pre[x1 - 1][y2] - pre[x2][y1 - 1] + pre[x1 - 1][y1 - 1];
cout << ans << '\n';
}
return;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}
4.二维差分
二维差分这个稍微难一点。
首先我们来看一下二维差分数组是什么样的
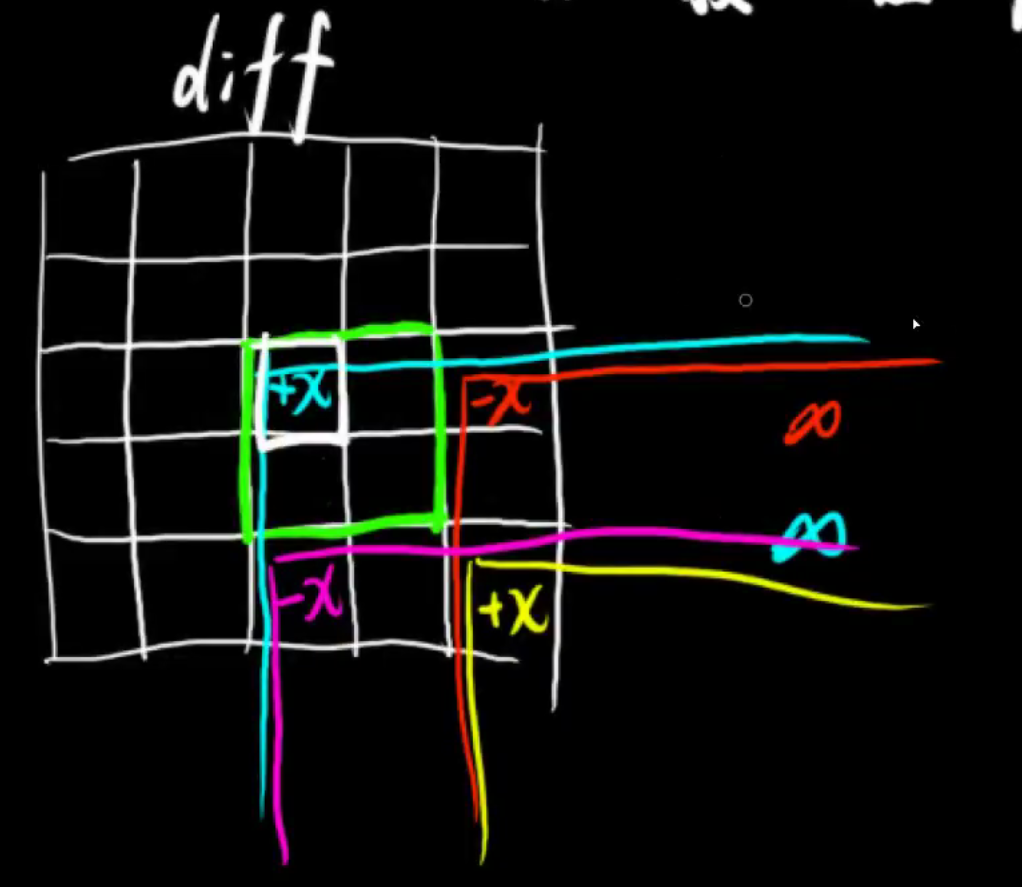
二维差分数组的计算与一维差分的有所不同。
一维差分数组我们是通过a数组直接计算出来的。
二维差分数组我们是在一个全为0的差分数组上,对每一个大小为1x1的矩形进行修改,将他修改为a[ i ][ j ]的值。
OK,来看题吧。
链接: 题目链接
题目描述
给定一个𝑛行𝑚列的整数矩阵。
有𝑞个操作,每个操作格式为:𝑥1,𝑦1,𝑥2,𝑦2,𝑐
其中(𝑥1,𝑦1)(𝑥2,𝑦2)
分别表示一个子矩阵的左上角和右下角的坐标,每个操作将对应的子矩阵的每个元素加上𝑐。
请输出进行完所有操作后的矩阵。
输入描述
第一行包括三个整数𝑛,𝑚,𝑞(1≤𝑛,𝑚≤1e3,1≤𝑞≤1e5)
输出描述
共𝑛行,每行包括𝑚个整数,表示进行完所有操作后的矩阵。
输入样例
4 3 3
1 5 1
3 3 2
5 3 4
4 4 2
1 2 1 2 2
2 1 2 3 2
4 2 4 3 1
输出样例
1 7 1
5 5 4
5 3 4
4 5 3
有一个问题,我们如何通过差分数组,对区间进行修改。
结合上面的图我们可以知道
diff[x1][y1] += c;
diff[x2 + 1][y1] -= c;
diff[x1][y2 + 1] -= c;
diff[x2 + 1][y2 + 1] += c;
即可实现对 [x1,y1] 到 [x2,y2] 区间的所有数字都加上一个 c 。
然后我们可以通过下面这个式子还原 a 数组。
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + diff[i][j];
好了,可以写代码了。
二维差分
//2024 jin
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 9;
ll a[N][N], pre[N][N], diff[N][N];//开ll
void solve()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
//将a的数据存入diff数组中
diff[i][j] += a[i][j];
diff[i + 1][j] -= a[i][j];
diff[i][j + 1] -= a[i][j];
diff[i + 1][j + 1] += a[i][j];
}
}
while (q--)
{
int x1, x2, y1, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
//对[x1,y1]到[x2,y2] 的区间进行修改。
diff[x1][y1] += c;
diff[x2 + 1][y1] -= c;
diff[x1][y2 + 1] -= c;
diff[x2 + 1][y2 + 1] += c;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
//还原成a数组
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + diff[i][j];
cout << a[i][j] << ' ';
}
cout << '\n';
}
return;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}
感谢你能看到这里。
第一次写博客,如有错误,还望各位不吝赐教。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号