感知机
目录
- 感知机模型
- 感知机模型的对偶形式
- 感知机算法实现
感知机模型
感知机是二分类的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯度下降法对损失函数进行最优化(最优化)。感知机的学习算法具有简单而易于实现的优点,分为原始形式 和 对偶形式。感知机预测是用学习得到的感知机模型对新的实例进行预测的,因此属于判别模型。感知机是一种线性分类模型,只适应于线性可分的数据,对于线性不可分的数据模型训练是不会收敛的。
定义(感知机): 假设输入空间(特征向量)是 $\chi\subseteq{R^n}$,输出空间为$Y=\{+1,-1\}$,输入$x\subseteq\chi$表示实例的特征向量,对应于输入空间的点;输出 $y\subseteq{Y}$表示实例的类别,则由输入空间到输出空间的表达形式为:
$$f(x)=sign(w*x+b)$$
称为感知机,其中$w$叫作权值,$b$叫作偏置。$sign$是符号函数,即:
$$sign(x)= \begin{cases} -1& {x<0}\\ 1& {x\geq 0} \end{cases}$$
感知机的几何解释:
线性方程$w \cdot x + b = 0$对应特征空间$R^n$中的一个超平面$S$,其中$w$是超平面的法向量,$b$是超平面的截距,这个超平面将特征空间划分为两个部分,位于两部分的点(特征向量)分别被分为正、负两类,因此,超平面$S$称为分离超平面。
数据集的线性可分性:
给定一个数据集$T={(x_1, y_1), (x_2, y_2),…,(x_N, y_N)}$,其中$x_i \in R^n$,$y_i \in \lbrace+1, -1 \rbrace$,$i=1,2,3,\dots,N$,若存在超平面$S$:$w \cdot x + b = 0$将数据集的正实例点和负实例点完全正确地划分到$S$的两侧,则称数据集$T$为线性可分数据集。
损失函数
假设训练数据线性可分,为了找到这个平面需要确定一个学习策略,即定义(经验)损失函数并将损失函数极小化,
为此,我们首先计算任意一点$x_0$到超平面$S$的距离:
$$d=\frac{|w \cdot x_0 + b |}{||w||}$$
这里,$||w||$是$w$的$L_2$范数。
其次,对于误分类数据来说,
$$ y_i(w \cdot x_0 + b )>0$$
损失函数是所有误分类点的集合:
$$L(w, b) = -\sum_{x_i \in M}y_i(w \cdot x_i + b)$$
感知机的优化方法
感知机学习算法是对以下最优化问题的算法。给定一个数据集:
$$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$$
使其为以下损失函数 极小化 问题的解:
$$L(w, b) = -\sum_{x_i \in M}y_i(w \cdot x_i + b)$$
感知机学习算法是误分类驱动的,具体采用随机梯度下降法(stochastic gradient descent)。首先任意选取一个超平面$w_0$,$b_0$,然后用梯度下降法不断地极小化目标函数.感知机模型选择的是采用随机梯度下降,这意味着我们每次仅仅需要使用一个误分类的点来更新梯度.
$$\nabla_wL(w, b) = -\sum_{x_i \in M}y_ix_i $$
$$\nabla_bL(w, b) = -\sum_{x_i \in M}y_i$$
原始形式
输入:训练数据集$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$
其中,$x_i \in \chi = R^{\ n}, \ y_i \in \gamma = \{+1, -1\}, \ i = 1, 2, ..., N$,学习率$\eta(0 < \eta \leq 1)$
输出:$w$,$b$,感知机模型$f(x)=sign(w*x+b)$
1.选出初值$w_0$,$b_0$
2.在训练集中选取数据$(x_i,y_i)$
3.如果$y_i(w\cdot x_i + b) \leq0$
$$w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i$$
4.转至 (2),直到训练集中没有误分类点。
感知机模型的对偶形式
对偶形式的想法是,将$w$ 和$b$ 表示为实例 $x_i$ 和标记 $y_i$的线性组合的形式,通过求解其系数而求得 $w$ 和$b$ 。不失一般性,可假设原始形式中初始值 $w_0$均$b_0$为 0。对误分类点$(x_i,y_i)$ 通过
$$w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i$$
逐步修改w 和$b$,设修改$n$ 次,则 关于 $(x_i,y_i)$ 的增量分别是 $\alpha_iy_ix_i 和 $\alpha_iy_i$和$\alpha_iy_ix_i $和 $\alpha_iy_i$,这里 $\alpha_i = n_i\eta$。最后得到的$w$ 和$b$, 可以分别表示为
$$w = \sum_{i = 1}^N\alpha_iy_ix_i \\ b = \sum_{i = 1}^N\alpha_iy_i$$
这里,$\alpha_i \geq 0, i = 1, 2, ..., N$
训练过程
输入:训练数据集$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$
其中,$x_i \in \chi = R^{\ n}, \ y_i \in \gamma = \{+1, -1\}, \ i = 1, 2, ..., N$,学习率$\eta(0 < \eta \leq 1)$
输出:$w$,$b$,感知机模型$f(x) = sign(\sum_{j = 1}^N\alpha_jy_jx_j \cdot x + b)$,其中$\alpha = (\alpha_1, \alpha_2, ..., \alpha_N)^T$
1. $\alpha \leftarrow 0, b \leftarrow 0$
2.在训练集中选取数据$(x_i,y_i)$
3.如果$y_i(\sum_{j = 1}^N\alpha_jy_jx_j \cdot x_i + b) \leq 0$,
$$\alpha_j \leftarrow \alpha_j + \eta \\b\leftarrow b + \eta y_i$$
4.转至 2,直到训练集中没有误分类点。
对偶形式中,可以预处理训练集中实例间的内积并以矩阵存储,该矩阵即 Gram 矩阵(Gram matrix)
$$G = [x_i \cdot x_j]_{N \times N}$$
感知机算法实现
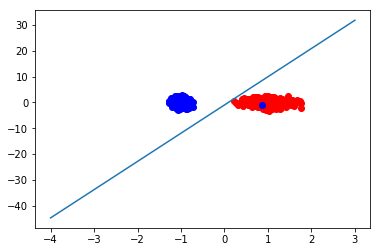
from sklearn.datasets import make_classification from sklearn.linear_model import Perceptron from sklearn.model_selection import train_test_split from matplotlib import pyplot as plt import numpy as np #利用算法进行创建数据集 def creatdata(): x,y = make_classification(n_samples=1000, n_features=2,n_redundant=0,n_informative=1,n_clusters_per_class=1) ''' #n_samples:生成样本的数量 #n_features=2:生成样本的特征数,特征数=n_informative() + n_redundant + n_repeated #n_informative:多信息特征的个数 #n_redundant:冗余信息,informative特征的随机线性组合 #n_clusters_per_class :某一个类别是由几个cluster构成的 make_calssification默认生成二分类的样本,上面的代码中,x代表生成的样本空间(特征空间) y代表了生成的样本类别,使用1和0分别表示正例和反例 y=[0 0 0 1 0 1 1 1... 1 0 0 1 1 0] ''' return x,y if __name__ == '__main__': x,y=creatdata() #将生成的样本分为训练数据和测试数据,并将其中的正例和反例分开 x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=0) #正例和反例 positive_x1=[x[i,0]for i in range(len(y)) if y[i]==1] positive_x2=[x[i,1]for i in range(len(y)) if y[i]==1] negetive_x1=[x[i,0]for i in range(len(y)) if y[i]==0] negetive_x2=[x[i,1]for i in range(len(y)) if y[i]==0] #定义感知机 clf=Perceptron(fit_intercept=True,n_iter=50,shuffle=False) # 使用训练数据进行训练 clf.fit(x_train,y_train) #得到训练结果,权重矩阵 weights=clf.coef_ #得到截距 bias=clf.intercept_ #到此时,我们已经得到了训练出的感知机模型参数,下面用测试数据对其进行验证 acc=clf.score(x_test,y_test)#Returns the mean accuracy on the given test data and labels. print('平均精确度为:%.2f'%(acc*100.0)) #最后,我们将结果用图像显示出来,直观的看一下感知机的结果 #画出正例和反例的散点图 plt.scatter(positive_x1,positive_x2,c='red') plt.scatter(negetive_x1,negetive_x2,c='blue') #画出超平面(在本例中即是一条直线) line_x=np.arange(-4,4) line_y=line_x*(-weights[0][0]/weights[0][1])-bias plt.plot(line_x,line_y) plt.show()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号