优化算法与参数调节

1. 模型与风险

 

 

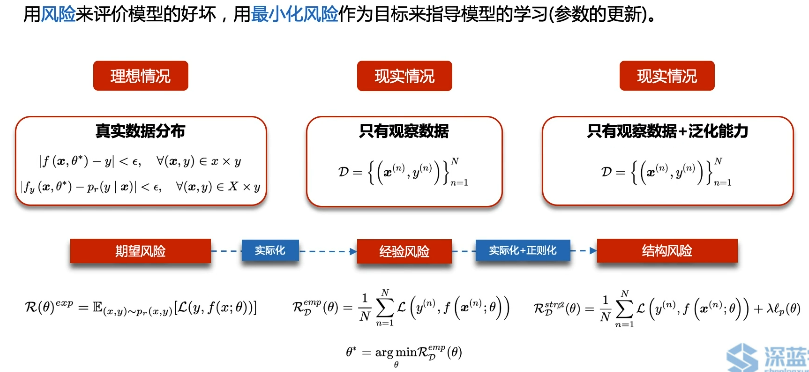
2. 损失函数

　　

3. 偏差与方差

　　偏差小，模型与最幽默型之间的差距就越小，即model拟合能力强

　　方差大，代表模型对不同数据集的分布学习的越好（过拟合），导致不同数据集训练出来的模型与模型的平均期望差距越大

　　通过正则项系数λ来控制偏差与方差之间的平衡

4. 评价指标

　　数据集划分：

　　训练集：用于训练模型

　　测试集：用于评估模型的最终能力，在整个训练过程中并没有用这一部分数据

　　验证集：用于调整和选择模型

　　传统的机器学习模型：倾向于使用K折交叉来完成模型选择与超参数的选取

　　神经网络模型：由于采用梯度下降方法，会随机从数据集D中划分训练集和测试集。并使用不同batch_size的数据集合进行训练，类似第二种数据集划分方法。

　　评价指标：

　　准确率、错误率：是在所有类别上整体的性能平均，由于数据类别的分布不平衡性，例如正负比例为9:1，那么模型只需要将所有样本全部分类为正例，也能获得90%的准确率。

　　精确率、召回率：对每个类别都进行性能的评估，真正例（TP），假正例（FP），假负例（FN），真负例（TN），精确率，所有预测为c的样本中预测正确的比例，召回率，所有真实标签为c的样本中预测正确的比例。

　　F值：综合指标，为精确率和召回率的调和平均（F1， belta = 1）

　　宏平均、微平均：计算分类算法在所有类别上的总体精确率、召回率和F1值，经常使用两种平均方法，即宏平均（每一类的性能指标的算术平均值）和微平均（每个样本的性能指标的算术平均值）

　　AUC、 ROC、 PR

5. 网络优化

　　梯度下降法：依据更新参数时使用的数据量大小，权衡时间和精度之后，有三种不同的梯度下降算法实现

 　   　　　　　　Batch Gradient Descent ,  Stochastic Gradient Descent,  Mini-batch Gradient Descent

　　1）BGD: 使用整个训练集合的所有样本点，优点：更新朝着正确的方向进行，保证收敛于极值，凸函数收敛于全局极值点； 缺点：学习时间长、消耗大量内存

　　2）SGD：对每个训练样本进行参数更新，优点：运行速度快，允许在线更新模型、会跳出局部极小值到另一个更好的局部极小值点； 缺点：每次更新可能不按照正确的方向进行、以较大的方差频繁更新，目标函数剧烈波动

　　3）MBGD：对使用的与样本量进行了权衡，即每次用多个样本组成的数据集来更新。优点：降低了参数更新的方差，获得更加稳定的收敛、可以使用矩阵优化； 缺点：学习率选择 困难、会陷入无限次的局部极小值或鞍点

　　几个概念：

　　Epoch：使用训练集全部数据对模型进行一次完整的训练，“一代训练”

　　Batch:使用一部分样本利用MBGD更新一次参数，“一批数据”

　　Iteration：使用一个Batch的数据对模型进行一次参数更新的过程，“一次训练”

 　　影响小批量梯度下降法的主要因素有：

　　　　　　批量大小-----批量大小越大，方差越小，噪声越小，训练越稳定，可以设置较大的学习率。----线性缩放原则（批量大小比较小时使用）

　　　　　　学习率-----过大，模型不收敛；过小，收敛太慢-----衰减（分段常数衰减、逆时衰减、指数衰减、自然指数衰减、余弦衰减），预热（最初几轮设置小一点，稳定性），周期性（逃离鞍点，局部极小值，循环学习率），自适应（根据不同参数的收敛情况分别设置学习率，AdaGrad, RMSprop, AdaDelta）等方法

　　　　　　梯度估计----考虑历史时刻平均梯度（Momentum,  Nesterov, Adam, 梯度截断法--梯度爆炸）