递归
1. 引子:汉诺塔
1.1 汉诺塔题目
古代某寺庙中有一个梵塔,塔内有3个座A、B和C,座A上放着64个大小不等的盘,其中大盘在下,小盘在上。有一个和尚想把这64 个盘从座A搬到座B,但一次只能搬一个盘,搬动的盘只允许放在其他两个座上,且大盘不能压在小盘上。现要求用程序模拟该过程,输入一个正整数n,代表盘子的个数,编写函数 void hanoi(int n,char a,char b,char c)
其中,n为盘子个数,从a座到b座,c座作为中间过渡,该函数的功能是输出搬盘子的路径。
输入格式:输入在一行中给出1个正整数n。
输出格式:输出搬动盘子路径。
#include<stdio.h>
void hanoi(int n, char a, char b, char c);
int main()
{
char a = 'a', b = 'b', c = 'c';
int n;
scanf("%d", &n);
hanoi(n, a, b, c);
}
void hanoi(int n, char a, char b, char c)
{
if (n == 1)
{
printf("%c-->%c", a, b);
}
else
{
hanoi(n - 1, a, c, b);
printf("\n%c-->%c\n", a, b);
hanoi(n - 1, c, b, a);
}
}
2. 思考
汉诺塔的问题看了答案才知道怎么做,到底应该怎么思考,解题逻辑是什么?
|
关键点1: |
如何把64个盘子简化成63个盘子。 |
|
(太难的题目,不应思考如何从1到2到3,而是明白此时n和n-1本质是一样的,不是企图从123的规律里得到答案,而是通过整体思想将n与(1到n-1)剥离,将n视为与n-1无差别,而后n→n-1→ …… →3→2→出口) |
|
|
关键点2: |
思考通式。 |
|
式1:n-1号盘子从a到c 式2:n号盘子a到b 式3:n-1号盘子c到b |
|
|
关键点三: |
出口/边界 |
3.发展:关于递归
3.1递归定义:
递归算法:一种直接或者间接调用自身函数或者方法的算法。
3.2 简单的举例(Fibonacci数列):
本题要求编写程序,利用数组计算菲波那契(Fibonacci)数列的前N项,每行输出5个,题目保证计算结果在长整型范围内。Fibonacci数列就是满足任一项数字是前两项的和(最开始两项均定义为1)的数列,例如::1,1,2,3,5,8,13,...。
输入格式:
输入在一行中给出一个整数N(1≤N≤46)。
输出格式:
输出前N个Fibonacci数,每个数占11位,每行输出5个。如果最后一行输出的个数不到5个,也需要换行。
如果输入的N不在有效范围内,则输出"Invalid."。
普通方法(循环):
#include<stdio.h>
int main()
{
int i,n;
scanf("%d", &n);
if (n < 1 || n>46)
{
printf("Invalid.");
}
else
{
int a = 1, b = 1;
int t;
for (i = 1; i <= n; i++)
{
if (i == 1)
{
printf("%11d", 1);
}
else
{
printf("%11d", b);
t = a;
a = b;
b = t + b;
if (i % 5 == 0)
{
printf("\n");
}
}
}
if (n % 5 != 0)
{
printf("\n");
}
}
}
递归方法:
#include<stdio.h>
int fibonacci(int n);
int main()
{
int i, n;
scanf("%d", &n);
if (n < 1 || n>46)
{
printf("Invalid.");
}
else
{
for (i = 1; i <= n; i++)
{
printf("%11d", fibonacci(i));
if (i % 5 == 0)
{
printf("\n");
}
}
if (n % 5 != 0)
{
printf("\n");
}
}
}
int fibonacci(int n)
{
if (n == 1 || n == 2)
{
return 1;
}
else
{
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
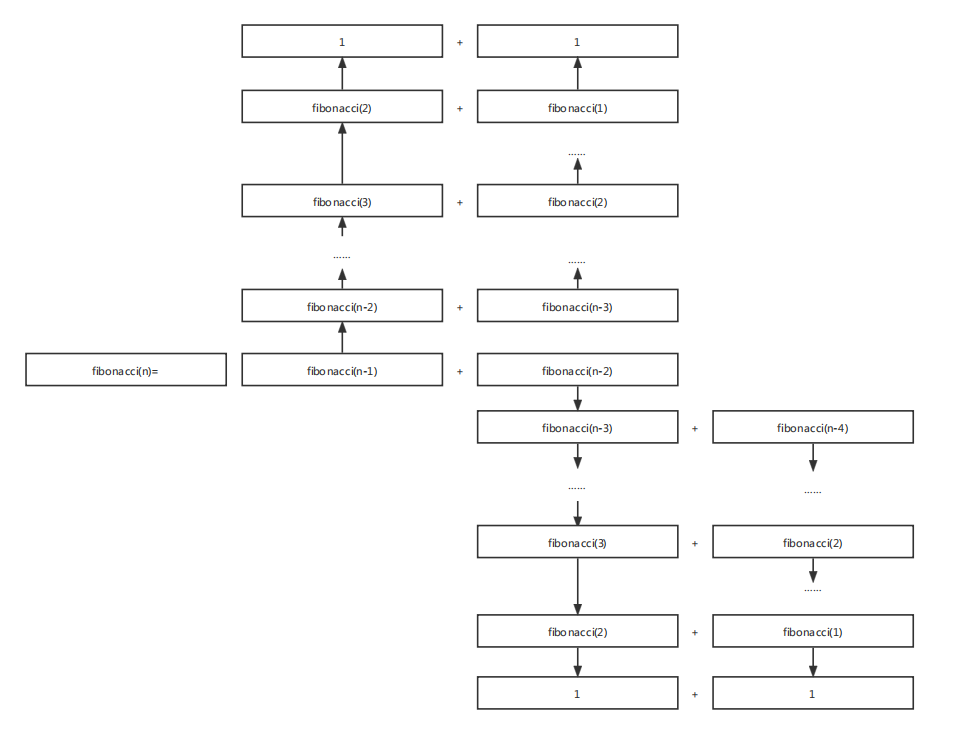
递归图解:
2.3 递归名声一直不好,why?
1. 时间和空间的消耗大。
每一个线程都会有一个私有的栈。每一次方法的调用都涉及到一个桢栈的入栈到出栈。同时,会涉及到分配内存空间,保存参数,返回地址和临时变量,而且往栈里压入数据和弹出都需要时间。
2. 递归会出现重复计算。
递归的本质是把一个问题分解为多个问题,如果多个问题存在重复计算,有时候这个情况会随着n成指数增长。比如斐波那契的递归就是一个例子。
比如上面递归:当n=50,时间为244.449s
3. 栈溢出的问题。
4.高潮:改进方法
动态递归:
将原问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。需要注意的是,动态递归会将每个求解过的子问题的解记录下来,这样当下一次遇到同样的子问题时,就可以直接使用之前记录的结果,而不是重复计算。
根据动态规划的特点,可以一解递归燃眉之急。
测试:n=50 用时:0.325s
#include<stdio.h>
#define ll long long
ll fibonacci(ll n);
ll str[100] = { 0 };
ll main()
{
ll i;
ll n;
scanf("%lld", &n);
printf("%lld", fibonacci(n));
}
ll fibonacci(ll n)
{
str[1] = 1; str[2] = 1;
if (n == 1 || n == 2)
{
return 1;
}
if (str[n] == 0)
{
str[n] = fibonacci(n - 1) + fibonacci(n - 2);
return str[n];
}
else
{
return str[n];
}
}
即函数调用出现在调用者函数的尾部, 所以根本没有必要去保存任何局部变量,直接让被调用的函数返回时越过调用者, 返回到调用者的调用者去。精髓:尾递归就是把当前的运算结果(或路径)放在参数里传给下层函数。
好处:函数的堆栈耗用难以估量,尾递归省去了保存中间函数堆栈的麻烦。
测试:n=50 用时:1.647
#include<stdio.h>
#define ll long long
ll fibonacci(ll n, ll a, ll b);
ll a = 1, b = 1;
int main()
{
ll n;
scanf("%lld", &n);
printf("%lld", fibonacci(n, a, b));
}
ll fibonacci(ll n, ll a, ll b)
{
if (n == 1)
{
return a;
}
else
{
return fibonacci(n - 1, b, a + b);
}
}
|
尾递归图解: Fibonacci ( n, a, b ); 初始值:n=5,a=1,b=1 |
||
|
Fibonacci(5,1,1) |
= |
Fibonacci(4,1,2) |
|
Fibonacci(4,1,2) |
= |
Fibonacci(3,2,3) |
|
Fibonacci(3,2,3) |
= |
Fibonacci(2,3,5) |
|
Fibonacci(2,3,5) |
= |
Fibonacci(1,5,8) |
|
Fibonacci(1,5,8) |
→ |
result=5 |
5.拓展:广度优先搜索
广度优先搜索本质也是迭代
5.1 步骤
- 输入数据
- dfs(根节点,带有根节点的v数组),定义result数组
- 在根节点的孩子节点中挑选a,dfs(a,带有根节点与子节点的v数组)
- 每次将v数组与result进行对比,如果v更长,则将result替换为当前v
- 当当前节点无孩子节点,则这一条搜索完毕。
- 当所有的路都搜索完毕,result数组则为所求。
5.2 例子(病毒溯源)
病毒容易发生变异。某种病毒可以通过突变产生若干变异的毒株,而这些变异的病毒又可能被诱发突变产生第二代变异,如此继续不断变化。
现给定一些病毒之间的变异关系,要求你找出其中最长的一条变异链。
在此假设给出的变异都是由突变引起的,不考虑复杂的基因重组变异问题 —— 即每一种病毒都是由唯一的一种病毒突变而来,并且不存在循环变异的情况。
输入格式:
输入在第一行中给出一个正整数 N(≤10^4),即病毒种类的总数。于是我们将所有病毒从 0 到 N−1 进行编号。
随后 N 行,每行按以下格式描述一种病毒的变异情况:
k 变异株1 …… 变异株k
其中 k 是该病毒产生的变异毒株的种类数,后面跟着每种变异株的编号。第 i 行对应编号为 i 的病毒(0≤i<N)。题目保证病毒源头有且仅有一个。
输出格式:
首先输出从源头开始最长变异链的长度。
在第二行中输出从源头开始最长的一条变异链,编号间以 1 个空格分隔,行首尾不得有多余空格。如果最长链不唯一,则输出最小序列。
注:我们称序列 { a1,⋯,an } 比序列 { b1,⋯,bn } "小",如果存在 1≤k≤n 满足 ai=bi 对所有 i<k 成立,且 ak<bk。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int>v[10001];
vector<int>result;
void Dfs(int now, vector<int>& p);
int main() {
int n;
int i, j, temp;
int root[10001] = { 0 };
cin >> n;
for (i = 0; i < n; i++) {
int m;
cin >> m;
for (j = 0; j < m; j++)
{
cin >> temp;
root[temp] = 1;
v[i].push_back(temp);
}
if (m)
{
sort(v[i].begin(), v[i].end());
}
}
for (i = 0; i < n; i++)
{
if (!root[i])
{
break;
}
}
vector<int> p;
p.push_back(i);
Dfs(i, p);
cout << result.size() << endl;
for (int i = 0; i < result.size(); i++) {
if (i) cout << " ";
cout << result[i];
}
}
void Dfs(int now, vector<int>& p)
{
if (p.size() > result.size())
{
result.clear();
result = p;
}
for (int i = 0; i < v[now].size(); i++) {
p.push_back(v[now][i]);
Dfs(v[now][i], p);
p.pop_back();
}
}
5.3 例题解析:
- 用两个循环输入数据到v中
- 因为题目要求"如果最长链不唯一,则输出最小序列",所以每次内循环完毕排个序
- root数组是为了寻根,数据中没有出现过的数据即为根节点,根节点推入p
- dfs(根节点,p)
- dfs中:
- 每次将v与result进行对比,若v长,则将result替换为v。
- 将当前节点替换为当前节点的孩子节点a,将a推入p,并进行递归dfs(节点a,p)
- 输入result数组
参考:
https://blog.csdn.net/weixin_45962741/article/details/116227551
https://blog.csdn.net/bolite/article/details/117405368


 浙公网安备 33010602011771号
浙公网安备 33010602011771号