RAG中的Re-Ranking[我们为什么要用Re-Ranking?]详解NSW、HNSW原理
引用原文:
一文彻底搞懂大模型 - RAG(检索、增强、生成)
Rerank——RAG中百尺竿头更进一步的神器,从原理到解决方案
深入浅出:理解RAG中的Re-Ranking机制
RAG之大模型常用向量数据库对比
HNSW算法的基本原理及使用
HNSW-分层可导航小世界 算法学习
RAG简介
RAG是什么
RAG(Retrieval-Augmented Generation,检索增强生成)是一种结合了信息检索、文本增强和文本生成的自然语言处理(NLP)的技术,其目的是通过从外部知识库检索相关信息来辅助大语言模型生成更准确、更丰富的文本内容。
RAG三大模块
-
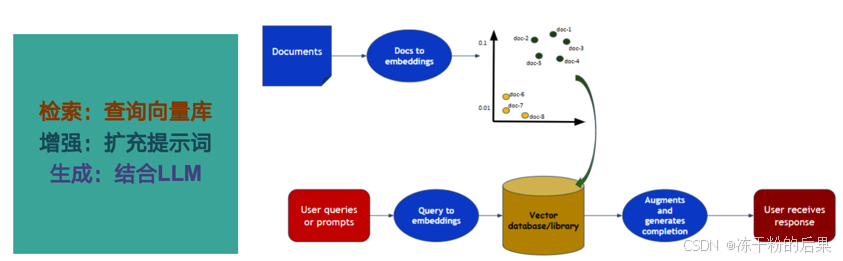
检索:检索是RAG流程的第一步,从预先建立的知识库中检索与问题相关的信息。这一步的目的是为后续的生成过程提供有用的上下文信息和知识支撑。
-
增强:RAG中增强是将检索到的信息用作生成模型(即大语言模型)的上下文输入,以增强模型对特定问题的理解和回答能力。这一步的目的是将外部知识融入生成过程中,使生成的文本内容更加丰富、准确和符合用户需求。通过增强步骤,LLM模型能够充分利用外部知识库中的信息。
-
生成:生成是RAG流程的最后一步。这一步的目的是结合LLM生成符合用户需求的回答。生成器会利用检索到的信息作为上下文输入,并结合大语言模型来生成文本内容。
![image]()
RAG构建步骤
1. 数据准备与知识库构建
-
收集数据: 首先,需要收集与问答系统相关的各种数据,这些数据可以来自文档、网页、数据库等多种来源。
-
数据清洗: 对收集到的数据进行清洗,去除噪声、重复项和无关信息,确保数据的质量和准确性。
-
知识库构建: 将清洗后的数据构建成知识库。这通常包括将文本分割成较小的片段(chunks),使用文本嵌入模型(如GLM)将这些片段转换成向量,并将这些向量存储在向量数据库中。
2. 检索模块设计
-
问题向量化: 当用户输入查询问题时,使用相同的文本嵌入模型将问题转换成向量。
-
相似度检索: 在向量数据库中检索与问题向量最相似的知识库片段(chunks)。这通常通过计算向量之间的相似度(如余弦相似度)来实现。
-
结果排序: 根据相似度得分对检索到的结果进行排序,选择最相关的片段作为后续生成的输入。
3. 生成模块设计
-
上下文融合:将检索到的相关片段与原始问题合并,形成更丰富的上下文信息。
-
大语言模型生成:使用大语言模型(如GLM)基于上述上下文信息生成回答。大语言模型会学习如何根据检索到的信息来生成准确、有用的回答。
RAG补充知识
RAG常用的向量数据库
Faiss:高效、灵活
-
关键词:高效性、灵活性、Facebook支持
-
功能特性:轻松将向量检索功能嵌入到深度学习,适合需要高效相似度搜索和丰富社区支持的大型应用
Milvus:大规模数据、云原生
-
关键词:大规模数据、云原生、高可用性
-
功能特性:大规模内容检索、图像和视频搜索,适合需要处理超大规模数据的云端应用
Chroma:轻量级、易用
-
关键词: 轻量级、易用性、开源
-
功能特性:快速搭建小型语义搜索,适合初学者和小型项目,专注于提供高效的近似最近邻搜索(ANN)
ANN
我们想象这么一个场景:你昨天刚在其他地方看到过一本新书,你想在图书馆找到类似的书。K-最近邻(KNN)算法的逻辑是浏览书架上的每一本书,并将它们从最相似到最不相似的顺序排列,以确定最相似的书(最有可能是你昨天看过的那本)。这也就是我们常说的暴力搜索,你有耐心做这么麻烦的工作吗?相反,如果我们对图书馆中的图书进行预排序和索引,要找到与你昨天看过的新书相似的书,你所需要做的就是去正确的楼层,正确的区域,正确的通道找到相似的书。
此外,你通常不需要对前10本相似的书进行精确排名,比如100%、99%或95%的匹配度,而是通通先拿回来。这就是近似近邻(ANN)的思想。你应该注意到了,这里已经出现了一些随机性——不做匹配分数的排名。但是这些准确度上的损失是为了让检索效率更快,为了显著降低计算成本,它牺牲了找到绝对最近邻的保证,这算是在计算效率和准确性之间取得平衡。
ANN算法目前主要有三种:
- 基于图的算法创建数据的图表示,最主要的就是分层可导航小世界图算法(HNSW)。
- 基于哈希的算法:流行的算法包括:位置敏感哈希(LSH)、多索引哈希(MIH);
- 基于树的算法:流行的是kd树、球树和随机投影树(RP树)。对于低维空间(≤10),基于树的算法是非常有效的。
ElasticSearch
- ES是一个开源的高扩展的分布式全文检索引擎,它可以近乎实时的存储、检索数据。主要功能就是搜索,如果在某个网站上需要用到搜索功能基本上都是用的ElasticSearch
- 我们可以使用ElasticSearch来实现RAG的向量搜索
- ElasticSearch的相似度算法用的就是HNSW
HNSW: 分层的最小世界导航算法(Navigable Small World Graphs)
概率跳表(Probability Skip List)
HNSW借鉴了跳表(Skip List)的思路。跳表是一种数据结构,用于维护一组已排序的元素,并允许进行高效的搜索、插入和删除操作。下图显示了数字[3、6、7、9、12、17、19、21、25、26]的排序链表。假设我们想找到目标19。当值小于目标时,我们向右移动,如果是传统的方式,需要6步才能找到它。

但是我们在每个节点增加向后的指向指针,比如列表中每三个其他节点都有一个指向后面三个节点的指针,如图所示,那么只需要3步就可以到达19

跳表每三个节点就设置一个多指向指针节点,可以让搜索速度明显加快,如果我们再增加这个指针节点数量呢?
这就是small world的底层思路
Small-World Networks(小世界网络)
小世界网络的概念由Duncan Watts和Steven Strogatz在1998年提出,他们的研究指出,许多现实世界的网络(如社交网络、神经网络、航空网络等)既不是完全随机的,也不是完全有序的,而是介于两者之间。这种网络模型可以解释现实生活中,某些网络虽然规模庞大,但个体之间的联系却可以通过少数几个中间人实现快速传播。这就是所谓的六度分隔理论(Six Degrees of Separation),即全球任何两个人之间都可以通过六个中间人联系在一起。
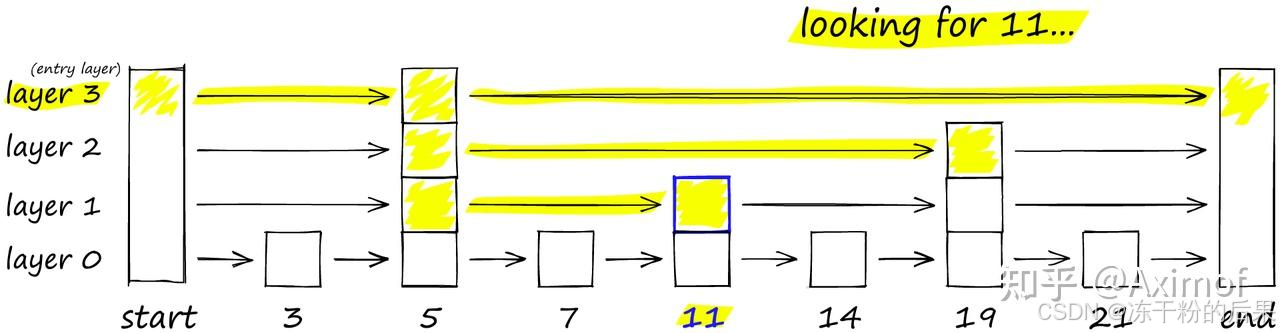
要搜索跳表,我们从具有最长跳跃的最高层开始,沿着边向右移动(如下图所示)。如果我们发现当前节点的 “键” 大于我们要搜索的键,就说明我们超过了目标,因此我们向下移动到下一层中的前一个节点。例如,图中搜索‘11’时,先从最高层layer3开始向右移动,一直到end节点没有查询到目标值,所以返回到‘5’键值的节点并向下移动到layer2开始搜寻;当在layer2移动到‘19’键值的节点时,发现超过了目标,因此返回到前一节点的leyer1层开始寻找,直到最终搜索到‘11’。
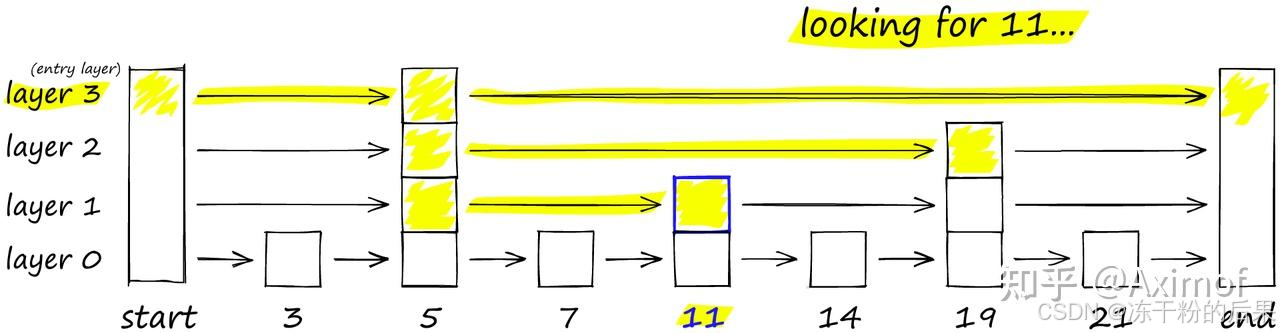
在概率跳表结构中,我们从顶层开始。如果我们当前的键大于我们要搜索的键(或者到达了末尾),我们就跳到下一层。
HNSW 继承了相同的分层格式,最高层的边长最长(用于快速搜索),而较低层的边长较短(用于准确搜索)。
NSW:可导航小世界图(Navigable Small World Graphs)
使用NSW图进行向量搜索的想法是:如果我们构建一个接近图,使其既具有长距离链接又具有短距离链接,那么搜索时间将降低到(poly/)对数复杂度。
图中的每个顶点连接到其他几个顶点。我们将这些连接的顶点称为vertices friends,并且每个顶点都保留一个verticesfriends列表,从而创建了我们的图。
在搜索 NSW 图时,我们从预定义的入口点开始。这个入口点连接到附近的几个顶点。我们确定其中与我们的查询向量最接近的顶点,并移动到该顶点。
通过贪婪地遍历每个vertices friends列表中的最近邻顶点,我们重复执行greedy-routing搜索过程,从顶点移动到顶点。最终,我们将找不到比当前顶点更近的顶点 - 这是一个局部最小值,也是我们的停止条件。
NSW->HNSW
HNSW 是 NSW 的自然演化,它从 Pugh 的概率跳表结构中汲取了灵感,添加了层级的概念。
向 NSW 中添加层级会产生一个图,其中的链接在不同的层之间分离。在顶层,我们拥有最长的链接,在底层,我们拥有最短的链接。
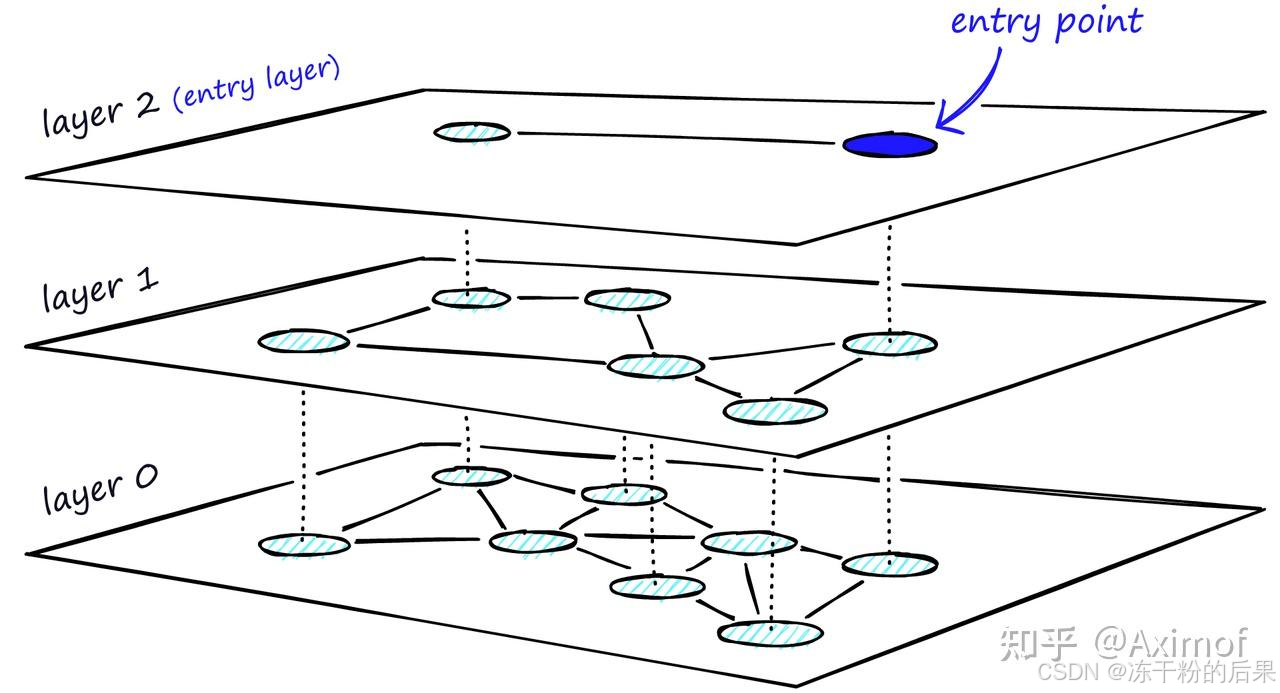
在搜索过程中,我们进入顶层,找到最长的链接。这些顶点往往是高度顶点(具有在多个层之间分离的链接),这意味着我们默认情况下会从 NSW 中的缩小阶段开始。
我们沿着每个层的边缘遍历,就像我们在 NSW 中所做的那样,贪婪地移动到最近的顶点,直到找到一个局部最小值。与 NSW 不同的是,此时我们转移到较低层中的当前顶点,并开始再次搜索。我们重复这个过程,直到找到底层(层 0)的局部最小值。
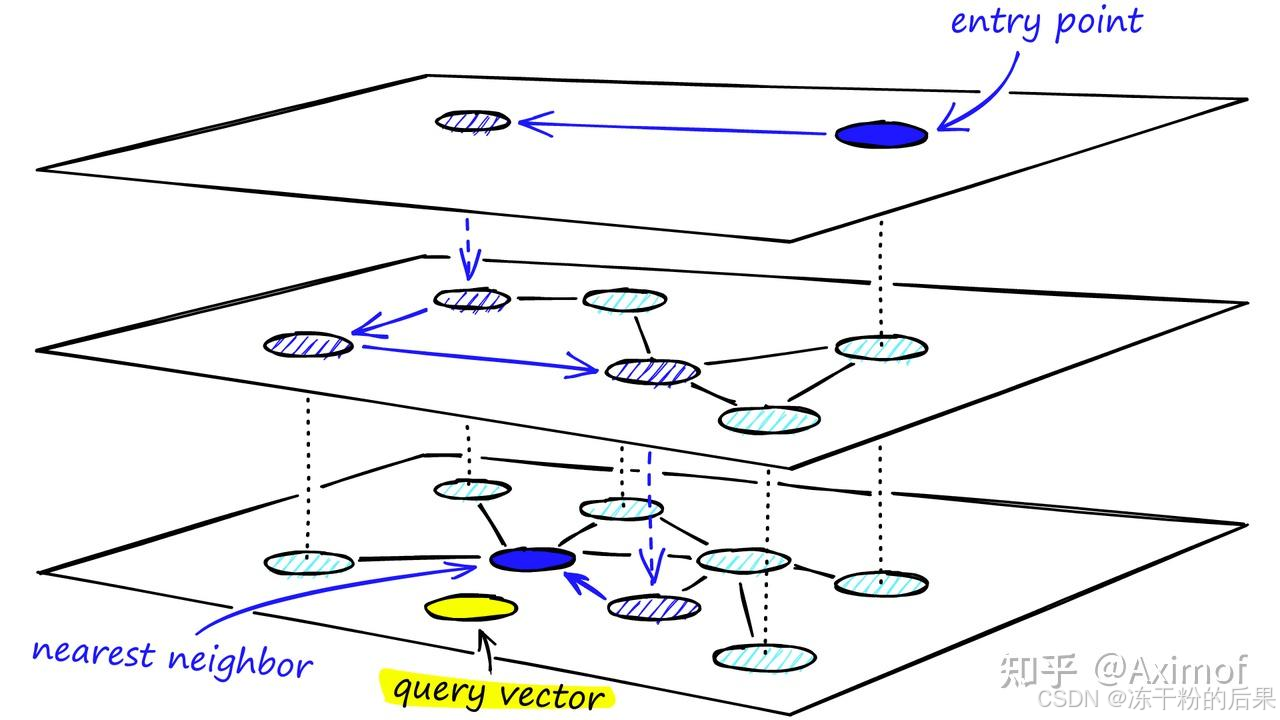
HNSW总结
HNSW是在NSW的基础上进行优化的结果,其引入了层级的概念,总体思想如下:
- 在Layer = 0层中,包含了连通图中所有的节点。
- 随着层数的增加,每一层的节点数逐渐减少并且遵循指数衰减定律。
- 图节点的最大层数,由随机指数概率衰减函数决定。
- 从某个点所在的最高层往下的所有层中均存在该节点。
- 在对HNSW进行查询的时候,从最高层开始检索。
“HNSW通过一个随机函数,将所有的点划分到不同层次”
为了检索的快速,HNSW算法会存在一些随机性,反映在实际召回结果中,最大的影响就是返回结果中top_K并不是我们最想要的,至少这K个文件的排名并不是我们认为的从高分到低分排序的。到这里,我们终于迎来了本文的主角——Re-Ranking。
因为在搜索的时候存在随机性,这应该就是我们在RAG中第一次召回的结果往往不太满意的原因。但是这也没办法,如果你的索引有数百万甚至千万的级别,那你只能牺牲一些精确度,换回时间。这时候我们可以做的就是增加top_k的大小,比如从原来的10个,增加到30个。然后再使用更精确的算法来做rerank,使用一一计算打分的方式,做好排序。比如30次的遍历相似度计算的时间,我们还是可以接受的。
Re-Ranking
Re-Ranking的定义和目的
Re-Ranking是指在RAG模型中对检索器返回的文档进行再排序的过程。其目的是通过重新排列候选文档,使得生成器更好地利用相关信息,并生成与输入问题更加相关和准确的结果。
在RAG中,Re-Ranking的关键目标是提高生成结果的相关性和质量。通过对检索器返回的文档进行再排序,Re-Ranking可以将与输入问题更加相关的文档排在前面,从而使得生成器在生成结果时能够更加准确地捕捉到输入问题的语境和要求,进而生成更加合适的答案或文本。
Re-Ranking评测步骤
Re-Ranking的过程可以分为以下几个步骤:
-
检索文档: 首先,RAG模型通过检索器从大规模语料库中检索相关文档,这些文档被认为可能包含了与输入问题相关的信息。
-
特征提取: 对检索到的文档进行特征提取,通常会使用各种特征,如语义相关性、词频、TF-IDF值等。这些特征能够帮助模型评估文档与输入问题的相关性。
-
排序文档: 根据提取的特征,对检索到的文档进行排序,将与输入问题最相关的文档排在前面,以便后续生成器使用。
-
重新生成: 排序完成后,生成器将重新使用排在前面的文档进行文本生成,以生成最终的输出结果。
评测方法
在RAG中,有多种方法可以实现Re-Ranking,包括但不限于:
-
基于特征的Re-Ranking: 根据检索到的文档提取特征,并利用这些特征对文档进行排序,以提高与输入问题相关的文档在排序中的优先级。
-
学习型Re-Ranking: 使用机器学习算法,如支持向量机(SVM)、神经网络等,根据历史数据和标注样本,学习文档与输入问题之间的相关性,并利用学习到的模型对文档进行再排序。
-
混合方法: 将基于特征的方法和学习型方法结合起来,以充分利用特征提取和机器学习的优势,从而更好地实现Re-Ranking的目标。
下面举一个Rerank——RAG中百尺竿头更进一步的神器,从原理到解决方案中的例子
为了衡量我们的检索系统的有效性,我们主要依赖于两个被广泛接受的指标:命中率和平均倒数排名(MRR)。让我们深入研究这些指标,了解它们的重要性以及它们是如何运作的。我们来解释一下这两个指标:
- 命中率:Hit rate计算在前k个检索文档中找到正确答案的查询比例。简单来说,它是关于我们的系统在前几次猜测中正确的频率。
- 平均倒数排名(MRR):对于每个查询,MRR通过查看排名最高的相关文档的排名来评估系统的准确性。具体来说,它是所有查询中这些秩的倒数的平均值。因此,如果第一个相关文档是顶部结果,则倒数排名为1;如果是第二个,倒数是1/2,以此类推。
常见re-ranking模型
- CohereAI
- bge-reranker-base
- bge-reranker-large
posted on 2025-06-30 16:33 Luminous_0601 阅读(445) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号