Manacher算法

1.1 概述

Manacher用于求解最长回文子串。一般情况下我们可能会想到时间复杂度为on3的暴力枚举，也很容易想到时间复杂度为on2的中心扩展法。Manacher算法是一种能在on的时间复杂度中求得最长回文子串的算法，Manacher就是优化后的中心检测法,和KMP算法类似,Manacher的思想也是避免"匹配"失败后的下标回退

1.2 详解

首先，我们得知道回文半径

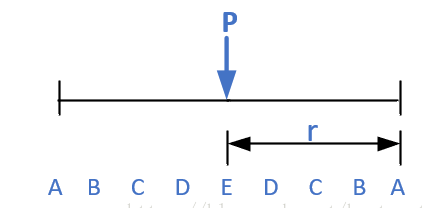
中心扩展法是依次枚举每一个点的回文半径,取所有回文半径的最大值.当当前字符满足回文条件的时候,检测下一个字符,否则返回当前半径长度,然后回文半径长度回退为1开始检测下一点。刚才我们说过Manacher算法其实是优化后的中心扩展法，也就是避免回退。那么如何避免回退呢？我们可以参考kmp算法建造一个数组来记录回退的最佳位置。len[i]表示以i为中心的回文串长度为len[i].
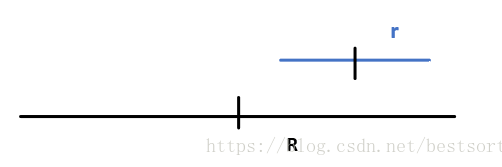
先设之前已经匹配好了left的最大回文半径长为R,然后设当前点right的回文半径为r,其中,r的起点一定大于R的起点(因为处理r的时候R已经处理好了)
那么R和r的关系一定有如下3种情况：

1. right+r <= left+R && right-r >=left (以right为中心的回文串在区间left~left+R之间)
   
   我们这里先给出r段关于R中心点所对称的线段r1
   
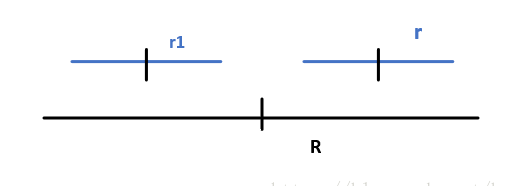
   len[r] = len[r1] = len[2*R-r]

2. right+r < left+R && right-r < keft
   
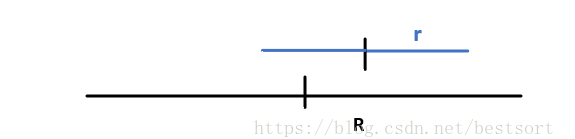
   还是和1一样，我们先画出关于R中心点对称的r1
   
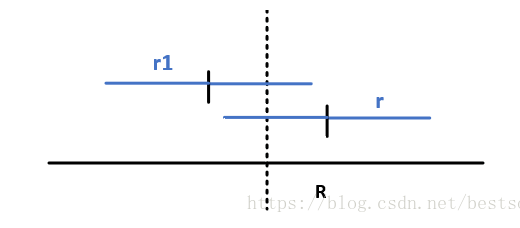
   len[r] = len[r1] = len[2*R-r]
   ​

3. right+r >left+R
   
   同样做对称
   
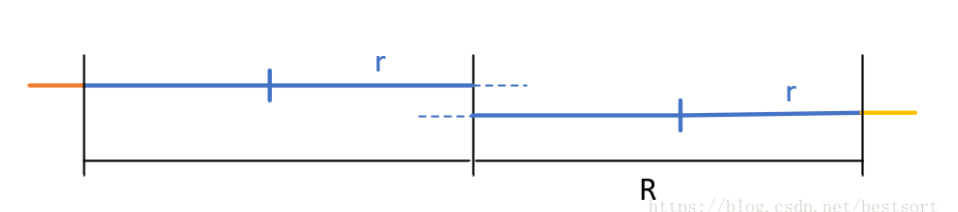
   有了上面的基础，我们现在唯一需要查询的就是黄线部分了，这里将回文半径由R继续扩大就好

到这里算法还有局限性，只能计算奇数串，所以我们还需要将原字符串处理一下。相邻字符间插入一个不在该字符串的字符集中的字符，比如$。原串长度为s，则转换后的串长度为2*s+1，所以必然为奇数。

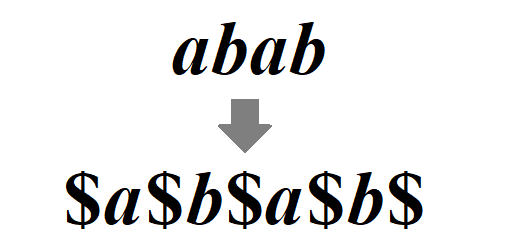
那么算出来的len和原字符串len的关系呢？len[i]-1就是以i为中心的最大回文长度。
在以i点为中点的回文长度为（2len[i]-1），半径为len[i]。设在其中的“#”有x个，其他字符有y个，则：
x + y = 2len[i] - 1
由于在每个字符前后都有一个“#”，显而易见“#”要比其他的字符多一个，则：
x-y=1
解以上两个方程得:
y= P[i] - 1

1.3代码

这里只是求出了len[]，然后根据自己的需要使用。

package manacherstring;

/**
 * JavaTest
 *
 * @author : xgj
 * @description : manacher算法
 * @date : 2020-08-19 12:56
 **/
public class ManacherString {
    public static char[] stringToCharArray(String s) {
        char[] chars = s.toCharArray();
        char[] res = new char[chars.length * 2 + 1];
        int index = 0;
        for (int i = 0; i < res.length; ++i) {
            res[i] = (i & 1) == 0 ? '#' : chars[index++];
        }
        return res;
    }

    public static int[] manacherArray(String str) {
        char[] charArr = stringToCharArray(str);
        int[] pArr = new int[charArr.length];
        int index = -1;
        int pR = -1;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < charArr.length; ++i) {

            pArr[i] = i < pR ? Math.min(pArr[2 * index - i], pR - i) : 1;

            while ((i + pArr[i] < charArr.length) && (i - pArr[i])>=0) {

                if (charArr[i + pArr[i]] == charArr[i - pArr[i]]) {
                    pArr[i]++;
                } else {
                    break;
                }
            }
            //更新回文右边界以及回文中心；
            if (i + pArr[i] > pR) {
                pR = i + pArr[i];
                index = i;
            }
            max = Math.max(max, pArr[i]);
        }
        return pArr;
    }
}