树状数组

引入问题：

给出一个长度为n的数组，完成以下两种操作。

• 将第x个数加上k
• 输出区间[x,y]内每个数的和

朴素算法O(n^2)：单点修改O(1),区间查询O(n)

树状数组处理O(nlog2^n): 单点修改（Olog2^n） 区间查询 O(log2^n)

 

lowbit()运算：

非负整数n在二进制表示下最低位1以及后面的0构成的数值

eg lowbit(44)=lowbit(101100)=(100)=4

 

思想与实现

• 将第x个数加上k
• 输出区间[x,y]内每个数的和

 

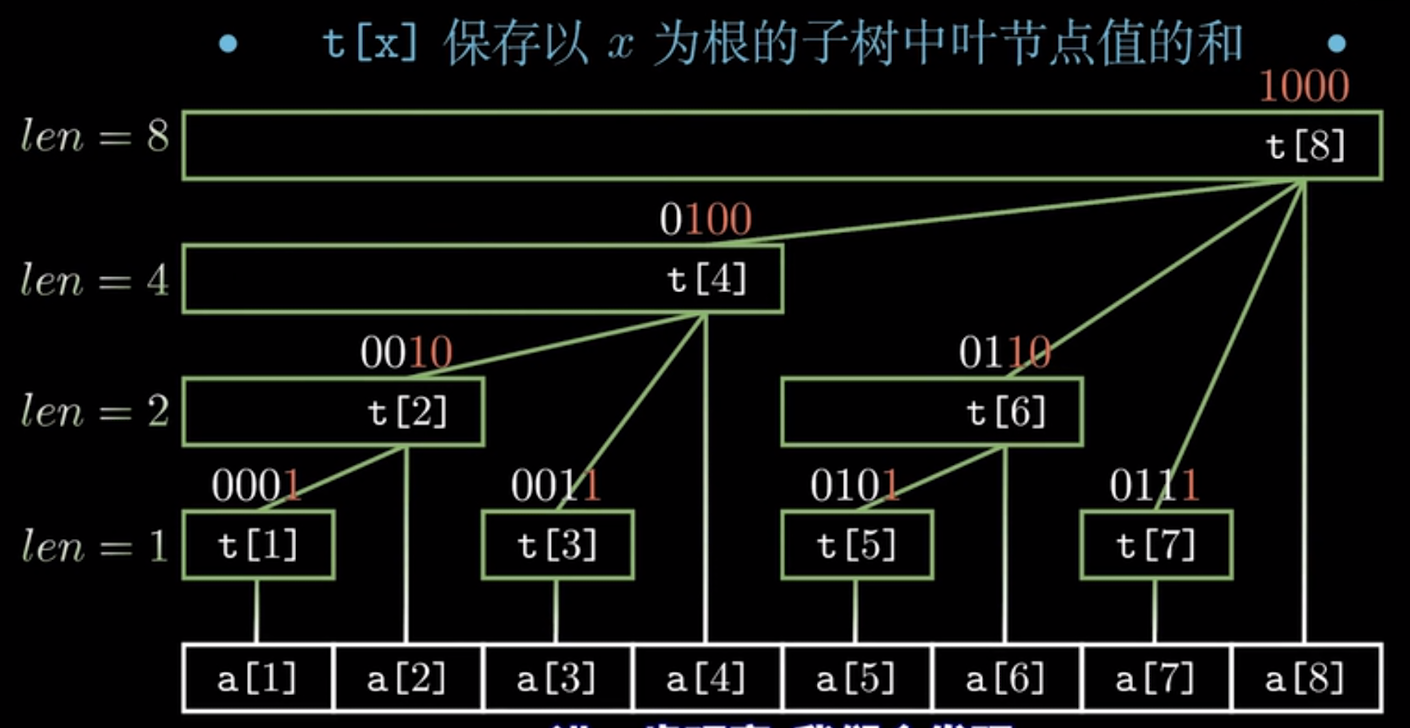
 进一步观察我们可以发现

• t[x]节点覆盖的长度就是lowbit(x)
• t[x]节点的父节点为t[x+lowbit[x]]
• 整颗树的深度为log2^n+1

add(x,k)操作

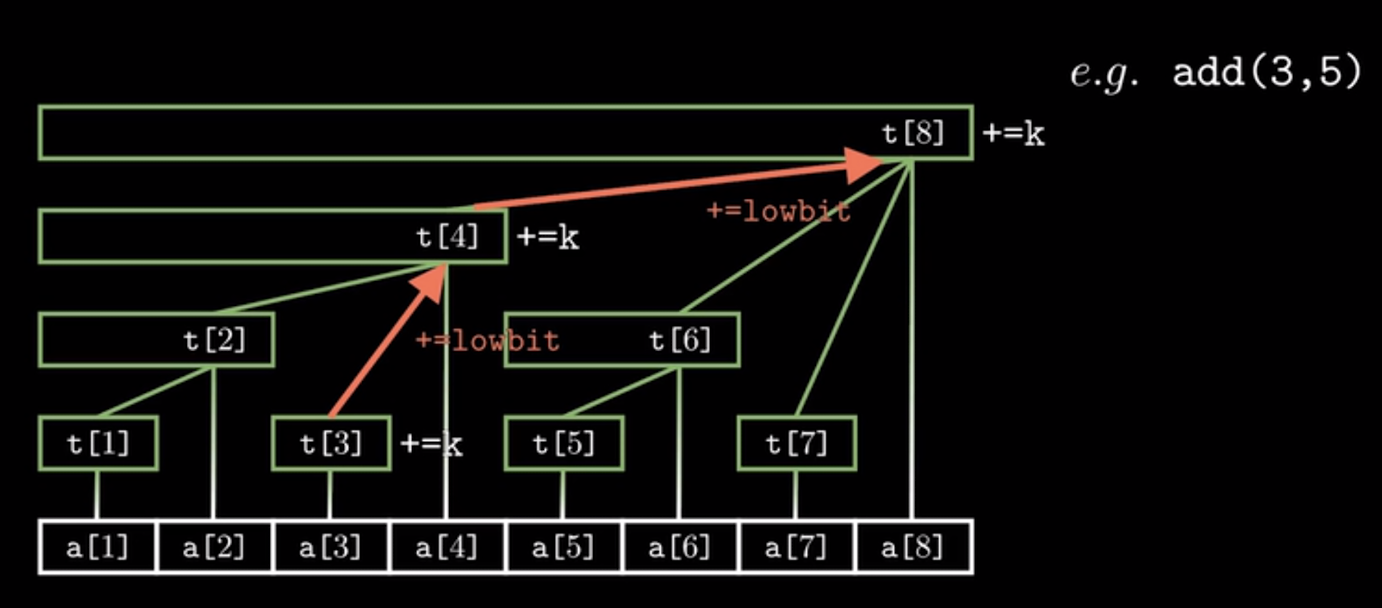
void add(int x,int k){
    for(;x<=n;x+=lowbit(x)) t[x]+=k;
}

 

ask(x)操作

 

 

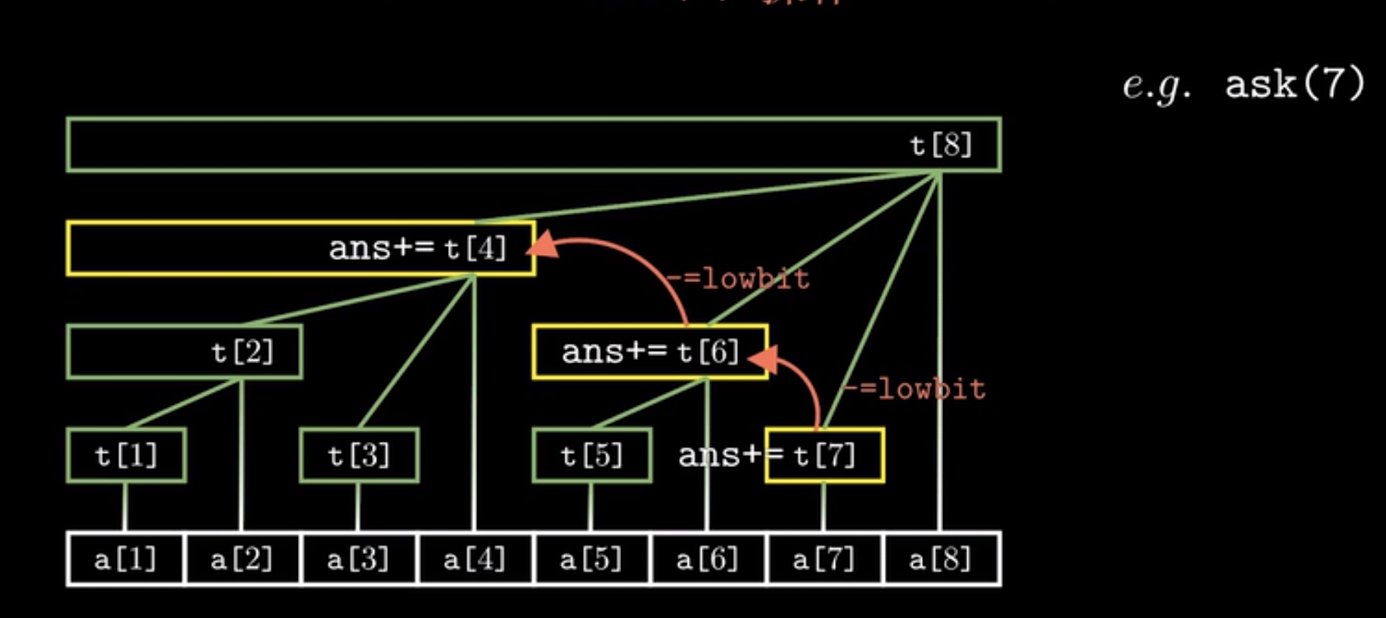
int ask(int x){
    int ans=0;
    for(;x;x-=lowbit(x)) ans+=t[x];
    return x;                  
}