跳表学习笔记
跳表概述
为啥会有跳表
跳表也是为了快速查找而提出的一种数据结构。细想我在此前学到的关于查找的知识。
- 有序数组用二分法,复杂度o(lgn)
- 对于树性结构,有BST, 平衡树, 平衡树又演化出很多结构,如B树, B+树,红黑树,AVL树。最好的时间复杂度是O(lgn)。
但是对于链表结构,却没有一种帮助我们快速查找的数据,链表时间复杂度是O(n), 跳表就产生了。它本质上是一种多级链表,通过增加数据的冗余来换取查找的时间复杂度,属于空间换时间的思想。不过呢,其实空间也不会消耗太多,因为冗余的只是节点指针。
优点分析
- 相比红黑树来说,跳表实现简单,你面试的时候是可以手写出来的,而且插入和删除的操作也不难。红黑树里面大量的自旋操作常常让人迷惑。
- 数据是自排序的,这点和MYSQL里面的B+树很像,默认是从小到大排序的。利用这一点就是快速进行范围查找,而不用真正地排序。
技术细节
结构
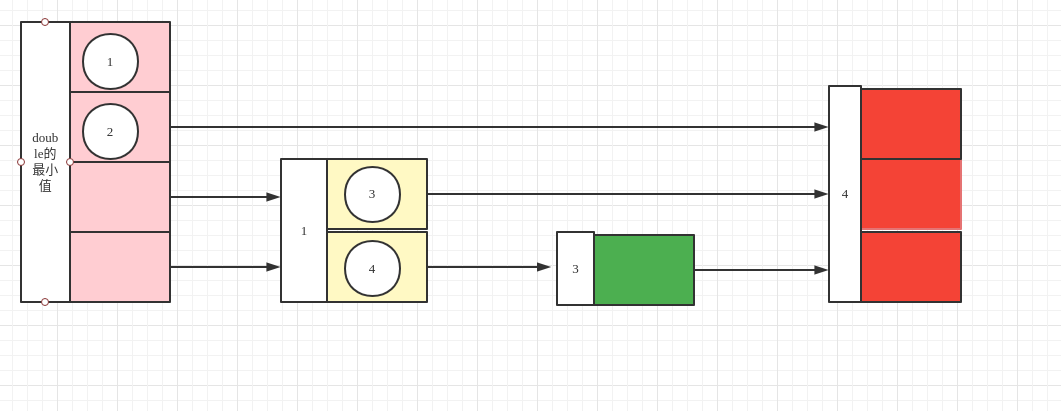
- 第一个粉色的位置是头节点,引入这个的作用是为了屏蔽一些插入和删除时的差异化。
- 最左侧表示节点的值, 可以看出,节点的值是从小到大排序的。
查找过程
例子:
我们以查找3的为例:
- 从头节点的最高层开始,也就是从节点1(图中用圆圈表示)开始,寻找第最后一个小于3的节点,找到了节点1。
- 节点1下移动一层,从节点2开始,寻找最后一个小于3的节点, 找到了节点3。
- 节点3下移动一层,从节点4开始, 寻找第一个小于3的节点开始,找到了节点4。
- 此时层数是0了,看节点4的下一个节点的值是否是3, 发现是的,就找到了,反之就找不到。
算法的优化: 可以在查找过程中,判断下一个节点是不是3, 如果是直接返回了,不必再深入了。
插入过程
我们以插入2为例子
插入2首先得生成一个随机高度,这个高度不得高于头节点的高度。这里可以用Java的random来实现。
- 首先进行一次查找,将小于2的节点都记录下来。 查找结束后,我们将节点1, 2, 3, 4 记录下来。
- 生成新的节点,同时设定新的节点的高度,这个可以通过随机生成,但是高度不得大于头节点的高度。
- 修改前后指针,主要改两个地方,新节点的下一个节点指针,新节点前面的节点指针。
- 节点4 的下一个节点改为节点4的下一个节点,节点4的下一个节点改为新节点。
- 节点6的下一个节点改为节点3的下一个节点,节点3的下一个节点改为新节点。
- 节点7 的下一个节点改为节点2的下一个节点,节点2的下一个节点改为新节点。
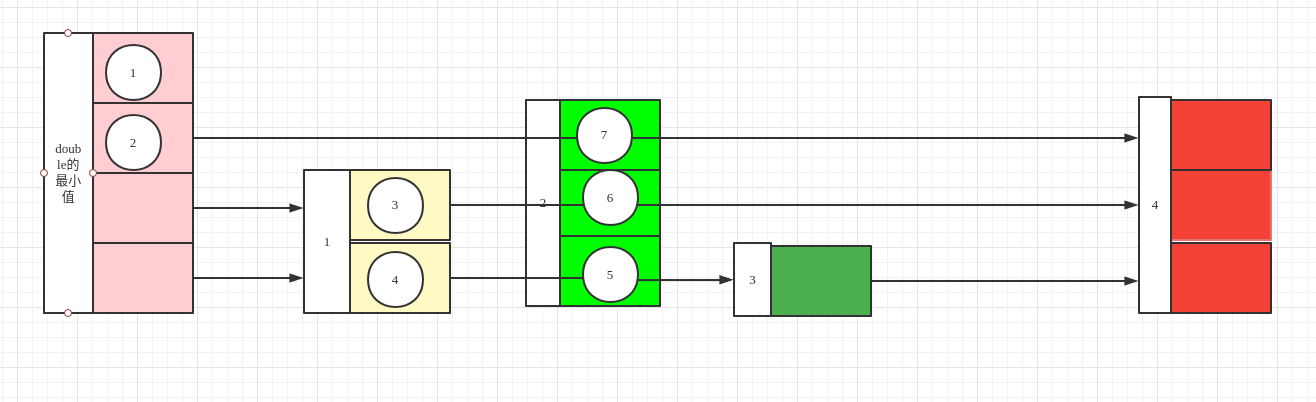
删除操作
删除操作和插入类似,也是现有一个查找的过程,只不过首先要看看在没在,如果不存在要删除的元素,则删除是失败的。在的话,更改节点指针。还是以下图为例子,我们要删除2。
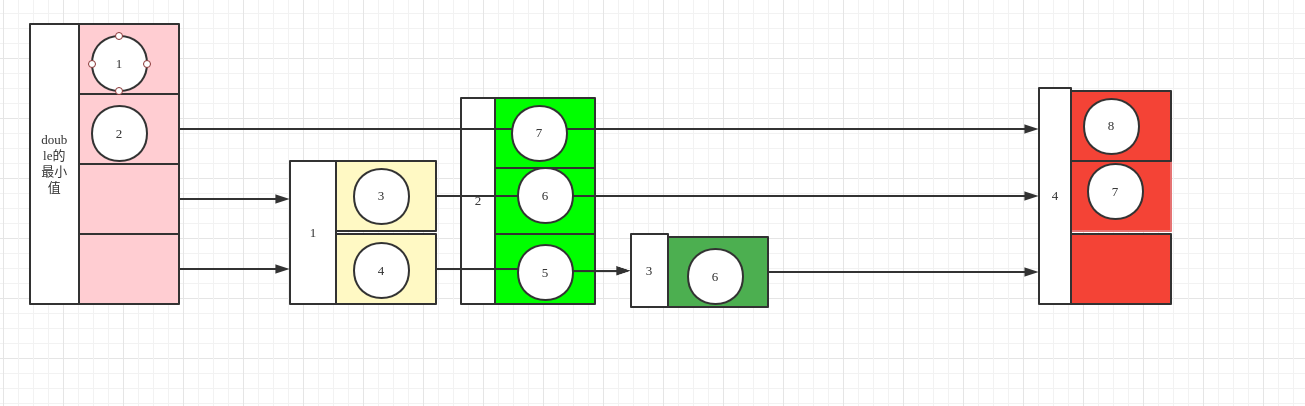
- 首先查找每一层比2小的节点,并记录下来。此时,我们将节点1, 2,3,4 记录下来
- 要删除的节点为值为2的这个节点,此时,我们修改这个节点的前置节点指针即可。
- 修改节点4的下一个节点为节点4的下一个节点的下一个节点,也就是节点6。
- 修改节点3的下一个节点为节点4的下一个节点的下一个节点。也就是节点7。
- 修改节点2的下一个节点为节点4的下一个节点的下一个节点。也就是节点8。
更新操作
更新一个值,如果我们直接更新以后,会导致跳表的调整,这个操作也比较复杂。比较好的一种思路,就是先删除再插入。这样就避免的调整操作,这个思路可以在编码时学习。
代码
最末尾
应用场景
redis 里面的zset就是采用了跳表的思想,只不过它不是真正的条表,而是跳表和hash的结合。
zset的要满足的功能主要有两个
- 要根据value 快速索引到score
- 可以根据score进行查找或者排序
这里,根据value快速索引到score是靠hash实现的,而根据score进行排序或者查找是通过跳表实现了。这个跳表底层是双向链表,其它层是单向的。这个层数默认是64层官方是做了优化的,可以保证跳表比较扁平化,使得上层的节点少一点,提高查询速度。
缺点与改进
- 这个缺点就是给每个节点分配层数的时候,可能都分配一些高度,导致链表出现每一层节点个数一样,这样时间复杂度就是普通链表差不多了。
/**
* @Author Fizz Pu
* @Date 2021/7/28 下午3:07
* @Version 1.0
* 失之毫厘,缪之千里!
*/
import java.lang.reflect.Array;
import java.util.*;
import java.util.concurrent.ThreadLocalRandom;
public class SkipListDemo {
// 最大高度
int MAX_LEVEL= 8;
public SkipListDemo(int maxLevel) {
this.MAX_LEVEL = maxLevel;
}
public SkipListDemo() {
}
private ThreadLocalRandom random = ThreadLocalRandom.current();
public static void main(String[] args) {
SkipListDemo skipList = new SkipListDemo();
// System.out.println(skipList.random.nextInt(0, 1));
skipList.insert(1);
skipList.insert(2);
skipList.insert(3);
System.out.println(skipList.find(1));
System.out.println(skipList.find(2));
System.out.println(skipList.find(3));
System.out.println(skipList.find(0));
System.out.println(skipList.delete(1));
System.out.println(skipList.delete(0));
System.out.println(skipList.delete(1));
System.out.println(skipList.find(1));
}
private Node head = Node.getHeadNode(MAX_LEVEL);
boolean find(int val) {
Node curNode = head;
Node nextNode;
int level = curNode.getLevel();
boolean isSkip; // 表示每一层链表是否有移动过
// 从头节点的最高层开始查找
while (level >= 1) {
isSkip = false;
// 寻找最后一个小于val的节点, 等价成链表操作
// 下一个节点存在并且小于val,才移动
while ((nextNode = curNode.next.get(level - 1)) != null && nextNode.val < val) {
curNode = nextNode;
isSkip = true;
}
nextNode = curNode.next.get(level-1);
if (nextNode != null && nextNode.val == val) {
return true;
}
// 更新level, 并下移
// 链表没有移动, 不用更新level, 直接减1
if (isSkip) {
level = curNode.getLevel();
}
level--;
}
nextNode = curNode.next.get(0);
if (nextNode == null) {
return false;
}
return nextNode.val == val;
}
int insert(int val) {
// 查找
int level = head.getLevel();
Node curNode = head;
Node nextNode;
boolean isSkip;
List<Node> nodes = new ArrayList<>();
while (level - 1 >= 0) {
isSkip = false;
while ((nextNode = curNode.next.get(level-1)) != null && nextNode.val < val) {
isSkip = true;
curNode = nextNode;
}
nodes.add(curNode);
if (isSkip) {
level = curNode.getLevel();
}
level--;
}
// 生成新的节点
int newNodeLevel = getLevel();
Node newNode = new Node(val);
// 修改后面和前面的节点
int counts = Math.min(newNodeLevel, nodes.size());
int nodesLen = nodes.size();
int end = nodesLen - counts;
int curLevel = 0;
Node tmp;
for (int i = nodesLen - 1; i >= end; i--) {
tmp = nodes.get(i);
newNode.next.add(tmp.next.get(curLevel));
tmp.next.set(curLevel, newNode);
curLevel++;
}
return 1;
}
int delete(int val) {
// 查找
int level = head.getLevel();
Node curNode = head;
Node nextNode;
boolean isSkip;
List<Node> nodes = new ArrayList<>();
while (level - 1 >= 0) {
isSkip = false;
while ((nextNode = curNode.next.get(level-1)) != null && nextNode.val < val) {
isSkip = true;
curNode = nextNode;
}
nodes.add(curNode);
if (isSkip) {
level = curNode.getLevel();
}
level--;
}
nextNode = curNode.next.get(0);
// 节点不存在
if (nextNode == null || nextNode.val != val) {
return 0;
}
// 开始删除
// 修改指针即可
int nextNodeLevel = nextNode.getLevel();
int counts = Math.min(nextNodeLevel, nodes.size());
int nodesLen = nodes.size();
int end = nodesLen - counts;
int curLevel = 0;
Node tmp;
for (int i = nodesLen - 1; i >= end; i--) {
tmp = nodes.get(i);
tmp.next.set(curLevel, nextNode.next.get(curLevel));
curLevel++;
}
nextNode = null; // help GC
return 1;
}
// 随机获得层数,但是不得大于MAX_LEVEL
protected int getLevel() {
if (MAX_LEVEL == 1) {
return 1;
}
return random.nextInt(1, MAX_LEVEL);
}
}
// 1 -> 2 -> 3 -> 4
class Node {
int val;
List<Node> next;
public static Node getHeadNode(int maxLevel) {
Node head = new Node(Integer.MIN_VALUE);
{
for (int i = 0; i < maxLevel ; i++) {
head.next.add(null);
}
}
return head;
}
public int getLevel() {
return next.size();
}
public Node(int val) {
this.val = val;
this.next = new ArrayList<>();
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号