可视化图解算法63：单词搜索

LeetCode 79. 单词搜索

1. 题目

描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

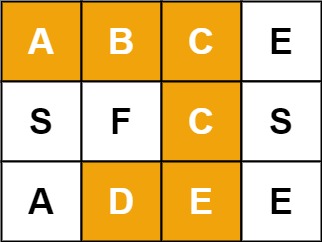
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

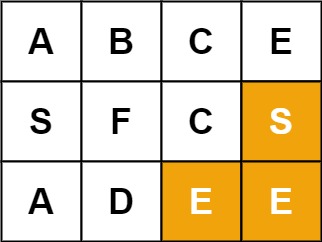
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

2. 解题思路

通过回溯实现单词的搜索。

如果文字描述的不太清楚，你可以参考视频的详细讲解。

• Python版本：https://www.bilibili.com/cheese/play/ep1374923
• Java版本：https://www.bilibili.com/cheese/play/ep1368187
• Golang版本：https://www.bilibili.com/cheese/play/ep1365129

3. 编码实现

核心代码如下：

var (
	row, column int
	visited     [][]bool
)

func exist(board [][]byte, word string) bool {
	row = len(board)
	column = len(board[0])
	visited = make([][]bool, row)
	for i := 0; i < row; i++ {
		visited[i] = make([]bool, column)
	}
	// 遍历二维网格的每一个点，作为搜索的起点
	for i := 0; i < row; i++ {
		for j := 0; j < column; j++ {
			if backtracking(board, word, i, j, 0) {
				return true
			}
		}
	}
	return false
}
func backtracking(board [][]byte, word string, i int, j int, index int) bool {
	//字符不相等，直接返回
	if !isValid(i, j) || board[i][j] != word[index] {
		return false
	}

	//3. 剪枝：如果字符已访问，直接返回
	if visited[i][j] {
		return false
	}

	//2.递归终止条件： 如果当前字符是字符串的最后一个字符，则找到了匹配项
	if index == len(word)-1 {
		return true
	}

	//1.选择：在本层集合中遍历元素
	//1.1 处理节点（ 标记当前位置为已访问）
	visited[i][j] = true
	// 1.2 递归（ 递归地在四个方向搜索）
	//向左
	if backtracking(board, word, i-1, j, index+1) {
		return true
	}
	//向右
	if backtracking(board, word, i+1, j, index+1) {
		return true
	}
	//向上
	if backtracking(board, word, i, j-1, index+1) {
		return true
	}
	//向下
	if backtracking(board, word, i, j+1, index+1) {
		return true
	}
	//1.3 回溯，撤销选择（将当前位置标记为未访问）
	visited[i][j] = false

	return false
}

func isValid(i int, j int) bool {
	return (i >= 0 && i < row) && (j >= 0 && j < column)
}

具体完整代码你可以参考下面视频的详细讲解。

• Python版本：https://www.bilibili.com/cheese/play/ep1374923
• Java版本：https://www.bilibili.com/cheese/play/ep1368187
• Golang版本：https://www.bilibili.com/cheese/play/ep1365129

4.小结

通过回溯实现单词搜索。步骤：二维网格的每一个点作为搜索的起点，搜索的时候采用回溯方法。1）将当前网格点设置为已访问过；2）到当前点的上、下、左、右四个方向递归尝试；3）回溯，撤销选择，即将当前网格点设置为未访问。

《数据结构与算法》深度精讲课程正式上线啦！7 大核心算法模块全解析：

  ✅   链表

  ✅   二叉树

  ✅   二分查找、排序

  ✅   堆、栈、队列

  ✅   回溯算法

  ✅   哈希算法

  ✅   动态规划

无论你是备战笔试面试、提升代码效率，还是突破技术瓶颈，这套课程都将为你构建扎实的算法思维底座。🔥立即加入学习打卡，与千名开发者共同进阶！

• Python编码实现：https://www.bilibili.com/cheese/play/ss897667807
• Java编码实现：https://www.bilibili.com/cheese/play/ss161443488
• Golang编码实现：https://www.bilibili.com/cheese/play/ss63997

对于LeetCode数据结构与算法，我们总结了一套【可视化+图解】方法，依据此方法来解决相关问题，算法变得易于理解，写出来的代码可读性高也不容易出错。具体也可以参考视频详细讲解。

今日佳句：老骥伏枥，志在千里；烈士暮年，壮心不已。