可视化图解算法39： 输出二叉树的右视图

1. 题目

描述

请根据二叉树的前序遍历，中序遍历恢复二叉树，并打印出二叉树的右视图

数据范围： 0≤n≤10000
要求： 空间复杂度 O(n)，时间复杂度 O(n)

如输入[1,2,4,5,3],[4,2,5,1,3]时，通过前序遍历的结果[1,2,4,5,3]和中序遍历的结果[4,2,5,1,3]可重建出以下二叉树：

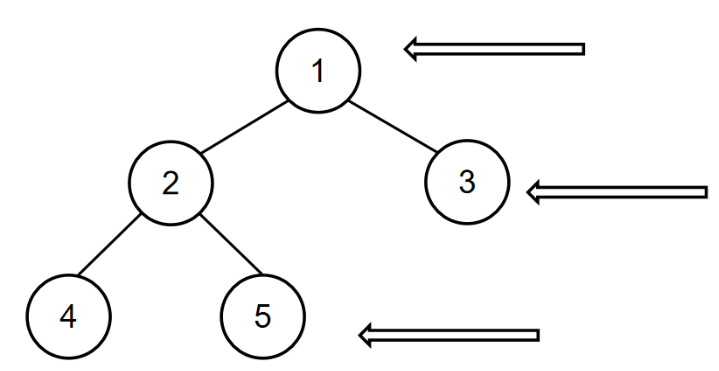
所以对应的输出为[1,3,5]。

示例1

输入：

[1,2,4,5,3],[4,2,5,1,3]

返回值：

[1,3,5]

2. 解题思路

本题其实包括两部分，即先根据前序遍历，中序遍历恢复二叉树，再并打印出二叉树的右视图。对于二叉树的回复可以参考上一篇文章《可视化图解算法38：重建二叉树》，本篇重点讲解如何打印出二叉树的右视图。

对于二叉树的右视图，可以先将二叉树进行层序遍历，对于层序遍历的结果，输出每一行的最后一个元素即可。二叉树的层序遍历可以参考《可视化图解算法23：二叉树的层序遍历》。

具体思路如下：

如果文字描述的不太清楚，你可以参考视频的详细讲解。

3. 编码实现

核心代码如下：

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 求二叉树的右视图
 * @param preOrder int整型一维数组 先序遍历
 * @param inOrder int整型一维数组 中序遍历
 * @return int整型一维数组
 */
func solve(preOrder []int, inOrder []int) []int {
	// write code here
	//构建二叉树
	tree := buildTree(preOrder, inOrder)
	//二叉树输出右视图
	return rightSideView(tree)
}

func rightSideView(root *TreeNode) []int {
	res := make([]int, 0)
	// 1. 定义一个队列，保存每一层的所有节点；先将根节点放入队列
	queue := []*TreeNode{root}
	//2. 执行出队列操作：出队列的左右子树再重新入队列
	for len(queue) > 0 {
		count := len(queue) //获取一层中的节点数量，并进行遍历
		//如果当前层有节点，将节点数据添加到数组中，左、右子树添加到队列中
		for i := 0; i < count; i++ {
			node := queue[0]  //获取队列的顶部元素
			queue = queue[1:] //删除队列的顶部元素
			if i == count-1 {
				res = append(res, node.Val) //存入右视图的元素：一行中的最后一个
			}
			//若是左右子节点存在，则存入左右节点作为下一个层次
			if node.Left != nil {
				queue = append(queue, node.Left)
			}
			if node.Right != nil {
				queue = append(queue, node.Right)
			}
		}
	}
	return res
}

func buildTree(pre []int, vin []int) *TreeNode {
	// 2. 递归终止条件（pre、vin长度一样，只需要判断一个即可）
	if len(pre) == 0 {
		return nil
	}
	// 1. 问题分解（递推公式）
	// 1.1 根节点（前序遍历的第一个值）
	root := &TreeNode{Val: pre[0]}
	// 1.2 根节点在中序遍历中的位置
	index := getIndex(vin, pre[0])
	// 1.3 以根节点索引为分割线，将数组pre、vin分为左右两部分
	root.Left = buildTree(pre[1:index+1], vin[:index])   //左部分构成左子树（切片截取：左闭右开）
	root.Right = buildTree(pre[index+1:], vin[index+1:]) //右部分构成右子树
	return root
}

func getIndex(vin []int, data int) int {
	for index, d := range vin {
		if d == data {
			return index //pre 和 vin 均无重复元素
		}
	}
	return 0
}

具体完整代码你可以参考下面视频的详细讲解。

4.小结

对于二叉树的右视图：①即先根据前序遍历，中序遍历恢复二叉树；②通过层序遍历再并打印出二叉树的右视图。

《数据结构与算法》深度精讲课程正式上线啦！七大核心算法模块全解析：

  ✅   链表

  ✅   二叉树

  ✅   二分查找、排序

  ✅   堆、栈、队列

  ✅   回溯算法

  ✅   哈希算法

  ✅   动态规划

无论你是备战笔试面试、提升代码效率，还是突破技术瓶颈，这套课程都将为你构建扎实的算法思维底座。🔥立即加入学习打卡，与千名开发者共同进阶！

对于二叉树的相关算法，我们总结了一套【可视化+图解】方法，依据此方法来解决相关问题，算法变得易于理解，写出来的代码可读性高也不容易出错。具体也可以参考视频详细讲解。

今日佳句：两岸猿声啼不住，轻舟已过万重山。

posted @ 2025-05-14 16:26  好易学数据结构  阅读(18)  评论(0)    收藏  举报