可视化图解算法33：判断是不是平衡二叉树

1. 题目

描述

输入一棵节点数为 n 的二叉树，判断该二叉树是否是平衡二叉树。

在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树

平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

样例解释：

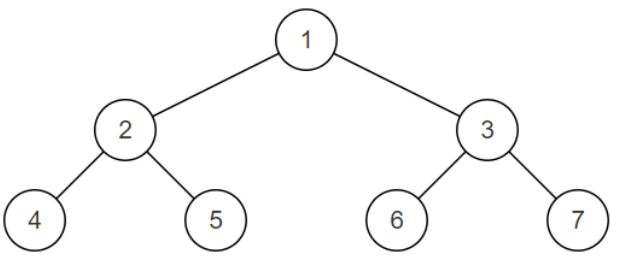
样例二叉树如图，为一颗平衡二叉树

注：我们约定空树是平衡二叉树。

数据范围：n≤100,树上节点的val值满足 0 ≤n≤1000

要求：空间复杂度O(1)，时间复杂度 O(n)

输入描述：

输入一棵二叉树的根节点

返回值描述：

输出一个布尔类型的值

示例1

输入：

{1,2,3,4,5,6,7}

返回值：

true

示例2

输入：

{}

返回值：

true

2. 解题思路

先来看平衡二叉树的性质：

平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

因此可以借助二叉树的高度来判断是否为平衡二叉树。整体思路为：先计算左右子树的高度，再比较左右子树的高度差（如果高度差大于1，则不是平衡二叉树）。

①对每一个节点的左右子树进行比较；②如果左子树不是平衡二叉树，就没有必要对右子树进行是否平衡的判断；③采用递归的方式对左右子树进行判断。

由于要采用递归来实现平衡二叉树的判断，因此需要验证是否满足递归的两个条件：

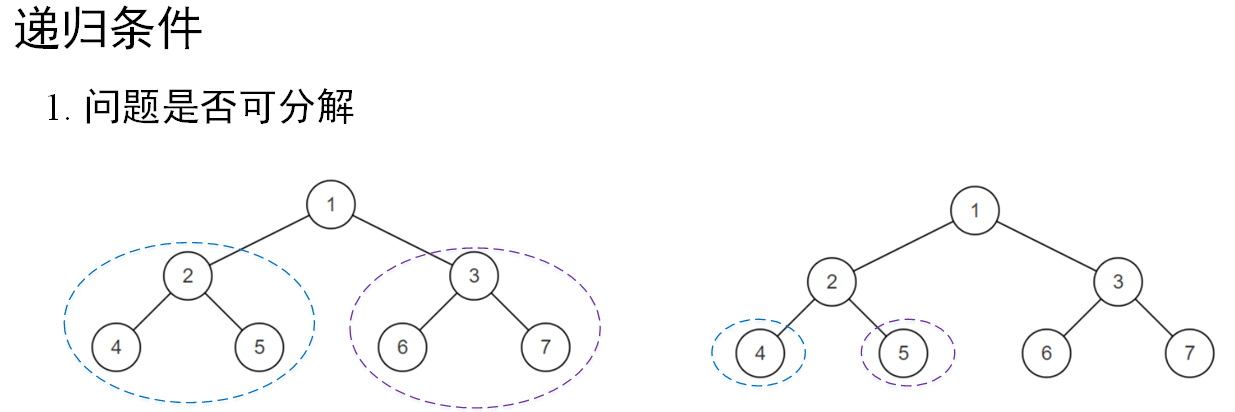
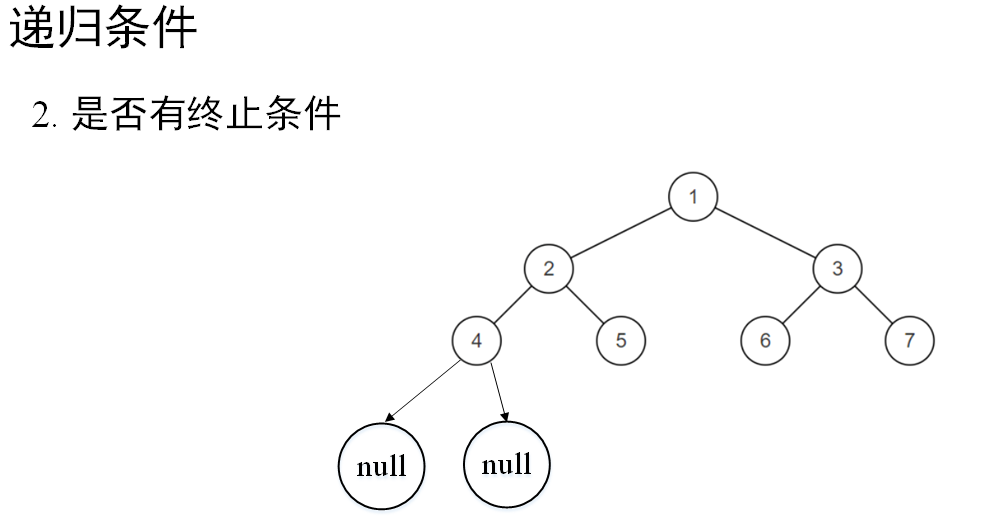
可以看出，求解二叉树平衡性的判断满足递归的两个条件，因此可以采用递归的方法来求解。由于平衡性的判断依赖于二叉树的高度，二叉树的高度求解参考前序文章《可视化图解算法25：二叉树的最大深度（高度）》，二叉树高度求解对应的递推公式如下：

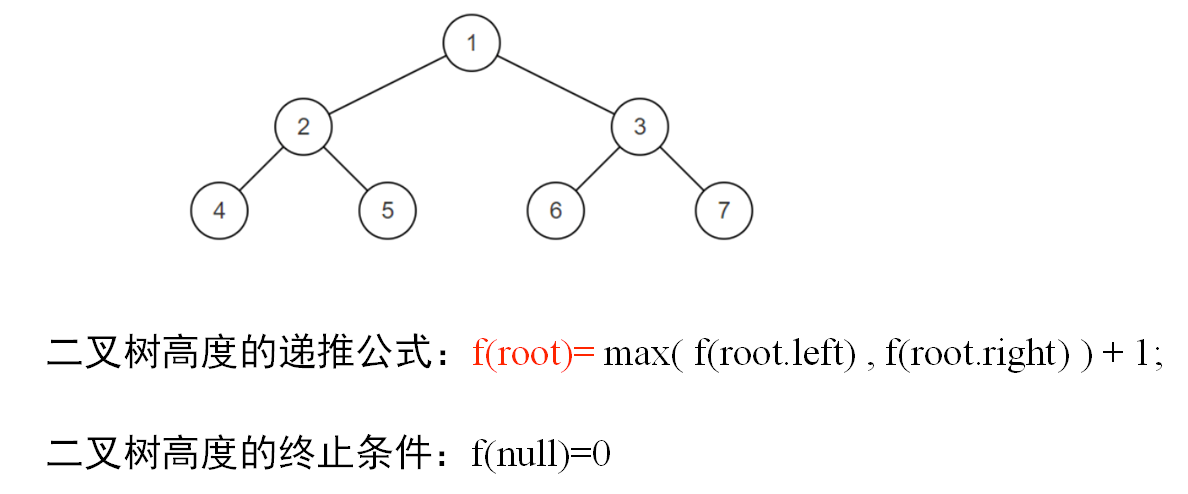
接下来就可以依据二叉树的高度进行平衡性的判断，先求解二叉树的左右子树的高度，再判断左右子树高度差是否超过1，如果超过1则不是平衡二叉树。

如果文字描述的不太清楚，你可以参考视频的详细讲解。

3. 编码实现

核心代码如下：

/**
* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
 * @return bool布尔型
*/
func IsBalanced_Solution(pRoot *TreeNode) bool {
	// write code here
	treeDepth(pRoot)
	return isBalanced
}

var isBalanced = true

func treeDepth(root *TreeNode) int {
	// 2. 递归终止条件
	if root == nil {
		return 0
	}

	// 1. 问题分解
	// 1.1 求解左子树的高度
	l := treeDepth(root.Left)
	// 1.2 求解右子树的高度
	r := treeDepth(root.Right)

	if math.Abs(float64(l-r)) > 1 {
		isBalanced = false // 不是平衡树,更改全局变量
		return -1          // 加一个标记-1，已经不可能是平衡树了（减少递归计算次数）,直接返回
	}
	// 1.3 求解当前树的高度
	dep := math.Max(float64(l), float64(r)) + 1
	return int(dep)
}

具体完整代码你可以参考下面视频的详细讲解。

4.小结

二叉树平衡性的判断，可以通过二叉树的高度来完成，即先求解二叉树的左右子树的高度，再判断左右子树高度差是否超过1，如果超过1则不是平衡二叉树。

《数据结构与算法》深度精讲课程正式上线啦！七大核心算法模块全解析：

  ✅   链表

  ✅   二叉树

  ✅   二分查找、排序

  ✅   堆、栈、队列

  ✅   回溯算法

  ✅   哈希算法

  ✅   动态规划

无论你是备战笔试面试、提升代码效率，还是突破技术瓶颈，这套课程都将为你构建扎实的算法思维底座。🔥立即加入学习打卡，与千名开发者共同进阶！

对于二叉树的相关算法，我们总结了一套【可视化+图解】方法，依据此方法来解决相关问题，算法变得易于理解，写出来的代码可读性高也不容易出错。具体也可以参考视频详细讲解。

今日佳句：长风破浪会有时，直挂云帆济沧海。

posted @ 2025-05-06 15:41  好易学数据结构  阅读(73)  评论(0)    收藏  举报