可视化图解算法31： 判断是不是二叉搜索树（验证二叉搜索树）

1. 题目

描述

给定一个二叉树根节点，请你判断这棵树是不是二叉搜索树。

二叉搜索树满足每个节点的左子树上的所有节点的值均严格小于当前节点的值；并且右子树上的所有节点的值均严格大于当前节点的值。

数据范围：节点数量满足 1≤n≤104 ，节点上的值满足 -231 ≤val≤231−1

示例1

输入：

{1,2,3}

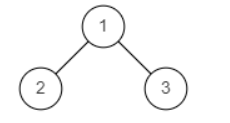
返回值：

false

示例2

输入：

{2,1,3}

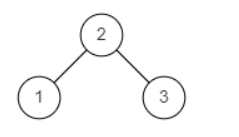
返回值：

true

2. 解题思路

先来看二叉搜索树的性质：

二叉搜索树（Binary Search Tree，简称BST）是一种特殊的二叉树，其每个节点的值都大于其左子树中所有节点的值并且小于其右子树中所有节点的值。二叉搜索树允许快速查询、插入和删除操作，多数操作（插入、删除和查找）的时间复杂度都是O(log n)。

以下是二叉搜索树的一些基本特性：

1.左子树的所有节点的值都小于其父节点。

2.右子树的所有节点的值都大于其父节点。

3.左、右子树也必须是二叉搜索树。

4.每个节点只有一个父节点（除了根节点）和最多两个子节点（左子节点和右子节点）。

判断一颗二叉树是否为二叉搜索树依赖于树的左右子树。可以采用递归的方法。

先来看看是否满足递归的两个条件：

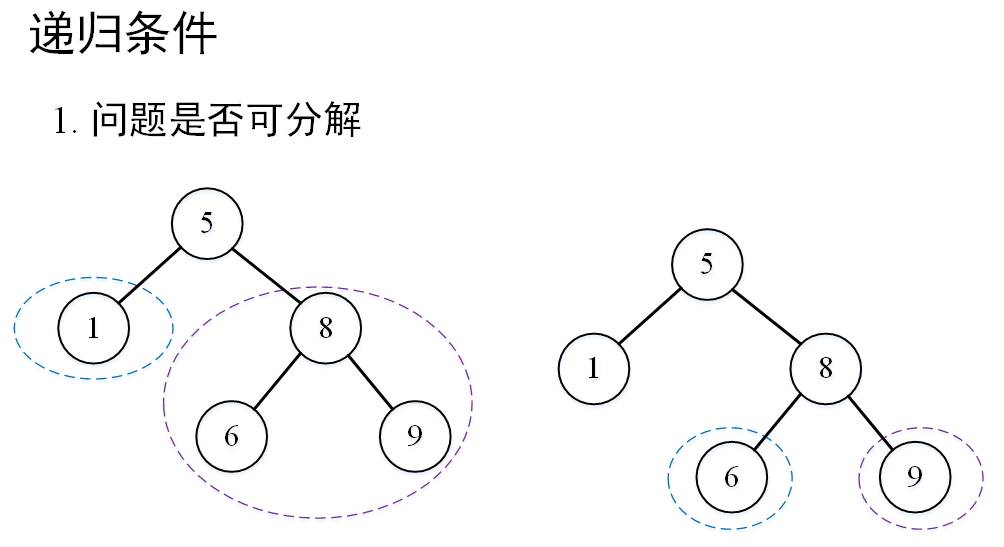
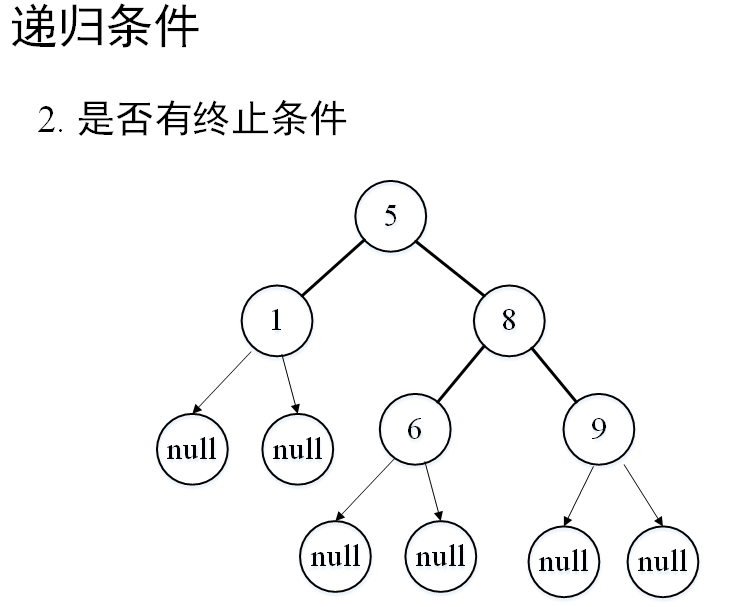
可以看出，判断二叉树是否为二叉搜索树的求解满足递归的两个条件，因此可以采用递归的方法进行求解。

一颗二叉树是否为二叉搜索树依赖于节点的左右子树。对于左子树，取值范围为：（-∞，root.val]；对于右子树，取值范围为： [root.val,+∞)。因此对应的递推公式如下：

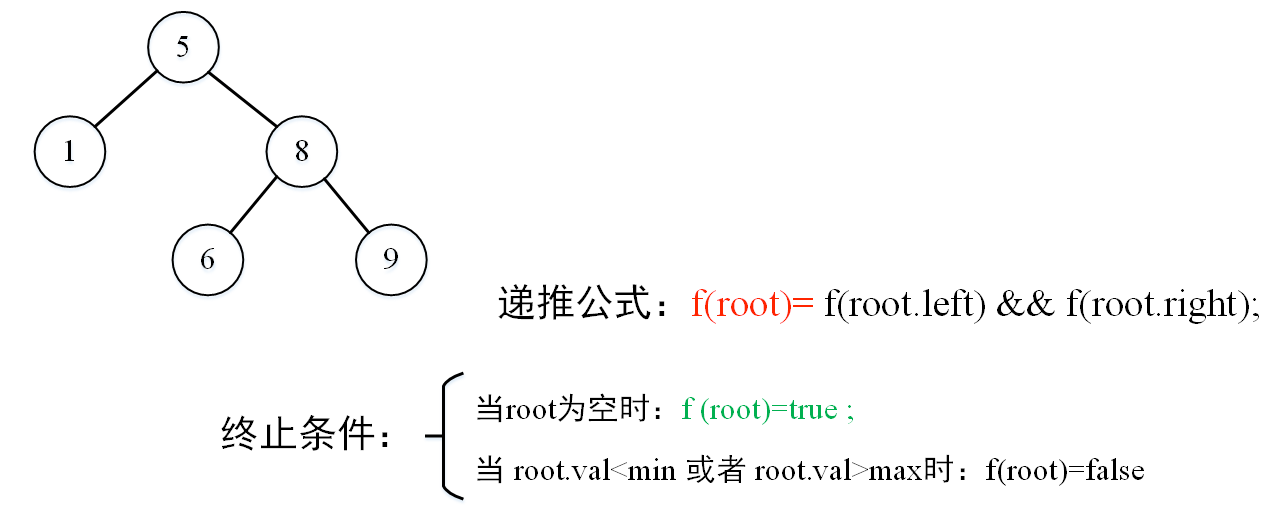
有了递推公式，就可以很方便的写出对应的代码。

如果文字描述的不太清楚，你可以参考视频的详细讲解。

3. 编码实现

核心代码如下：

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param root TreeNode类
 * @return bool布尔型
 */
func isValidBST(root *TreeNode) bool {
	// write code here

	return recursion(root, math.MinInt32, math.MaxInt32) //对于二叉树来说，取值范围为：(-∞,+∞)
}

func recursion(root *TreeNode, min int, max int) bool {
	// 2. 递归终止条件:
	// 2.2 如果二叉树为空，是搜索二叉树
	if root == nil {
		return true
	}
	// 2.2 如果当前节点的值小于min或者 大于max，则不是二叉搜索树
	if root.Val < min || root.Val > max {
		return false
	}

	// 1. 问题分解（递推公式）
	//左子树取值范围：(min,root.val]；	右子树取值范围：[root.val,max)
	return recursion(root.Left, min, root.Val) && recursion(root.Right, root.Val, max)
}

具体完整代码你可以参考下面视频的详细讲解。

4.小结

判断一颗二叉树是否为二叉搜索树依赖于树的左右子树。可以采用递归的方法。对于节点的左子树，取值范围为：（-∞，root.val]；对于节点的右子树，取值范围为： [root.val,+∞)。

《数据结构与算法》深度精讲课程正式上线啦！七大核心算法模块全解析：

  ✅   链表

  ✅   二叉树

  ✅   二分查找、排序

  ✅   堆、栈、队列

  ✅   回溯算法

  ✅   哈希算法

  ✅   动态规划

无论你是备战笔试面试、提升代码效率，还是突破技术瓶颈，这套课程都将为你构建扎实的算法思维底座。🔥立即加入学习打卡，与千名开发者共同进阶！

对于二叉树的相关算法，我们总结了一套【可视化+图解】方法，依据此方法来解决相关问题，算法变得易于理解，写出来的代码可读性高也不容易出错。具体也可以参考视频详细讲解。

今日佳句：长安回望绣成堆，山顶千门次第开。

posted @ 2025-04-29 16:38  好易学数据结构  阅读(14)  评论(0)    收藏  举报