义乌集训7.12 contest 5题解
2021.7.12 Contest 题解
T1:
Description:
给定序列 \(a_1,a_2,...,a_n\) ,算出 \(t_1,t_2,...,t_n\) 满足
- \(\forall t_i\gt0\);
- 对于所有的 \(i\) \((1\le i\lt n)\) , \(a_i*a_{i+1}*t_i*t_{i+1}\) 是完全平方数;
- \(\Pi_{i=1}^n t_i\) 最小。
请输出最小的 \(\Pi_{i=1}^n t_i\)
Input:
第一行一个整数 \(n\) 。
第二行 \(n\) 个整数 \(a_1,a_2,...,a_n\)。
Output:
一行一个数表示答案。请输出答案 mod \(10^9+7\)。
Sample1 Input:
3
2 3 6
Sample1 Output:
6
Hint:
对于所有数据,\(1\leq n \leq 10^5,1 \leq a_i \leq 10^6\)。
题目分析:
显然,每个质因数可以分开考虑。
对于某一个质因数 \(p\) ,如果 \(a_i\) \((1\leq i<n)\)和 \(a_{i+1}\)中含有 \(p\) 的次数为奇数,则 \(t_i\) 与 \(t_{i+1}\) 中必有一个且仅有一个含有 \(p\) 作为因数;反之,\(t_i\) 和 \(t_{i+1}\) 要么都含有该因数,要么都没有。
于是,对于 \(p\) ,问题转化为一个黑白染色的问题,强制 \(t_1\) 含有 \(p\) ,则 \(t_2,t_3,……,t_{n-1}\) 是否含有 \(p\) 都已确定,若含 \(p\) 的个数比不含 \(p\) 的个数多,则强制 \(t_1\) 不含有 \(p\),原来含 \(p\) 的 \(t_i\) 都不含 \(p\) ,不含 \(p\) 的 \(t_i\) 都含 \(p\) 。
总之就是个贪心选取的过程。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 100005
#define M 1000005
using namespace std;
int n,tot,ans=1,S[M][2],pp[22],op[M],lst[M],pri[M],len[M],P[M][11],K[N][11],A[N][11],T[N],kk[M];bool ok[M];const int p=1e9+7;
inline int power(int x,int y){int z=1;while(y){if(y&1) z=1ll*z*x%p;y>>=1,x=1ll*x*x%p;}return z;}
struct FastIO{
static const int S=1048576;
char buf[S],*L,*R;int stk[20],Top;~FastIO(){clear();}
inline char nc(){return L==R&&(R=(L=buf)+fread(buf,1,S,stdin),L==R)?EOF:*L++;}inline void clear(){fwrite(buf,1,Top,stdout);Top=0;}
inline void pc(char ch){Top==S&&(clear(),0);buf[Top++]=ch;}inline void endl(){pc('\n');}
FastIO& operator >> (char&ch){while(ch=nc(),ch==' '||ch=='\n');return *this;}
template<typename T>FastIO& operator >> (T&ret){
ret=0;int f=1;char ch=nc();while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=nc();}
while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=nc();}ret*=f;return *this;
}
FastIO& operator >> (char* s){int Len=0;char ch=nc();while(ch!='\n'){*(s+Len)=ch;Len++;ch=nc();}}
template<typename T>FastIO& operator << (T x){
if(x<0){pc('-');x=-x;}do{stk[++stk[0]]=x%10;x/=10;}while(x);
while(stk[0]) pc('0'+stk[stk[0]--]);return *this;
}
FastIO& operator << (char ch){pc(ch);return *this;}
FastIO& operator << (string str){int Len=str.size()-1;for(stk[0]=0;Len>=0;Len--) stk[++stk[0]]=str[Len];while(stk[0]) pc(stk[stk[0]--]);return *this;}
}fin,fout;
int main(){
freopen("square.in","r",stdin);freopen("square.out","w",stdout);
fin>>n;for(register int i=2;i<=M-5;i++){if(ok[i]) continue;pri[++tot]=i,P[i][++len[i]]=i;for(register int j=i*2;j<=M-5;j+=i) ok[j]=1,P[j][++len[j]]=i;}
for(register int i=1,x;i<=n;i++){fin>>x;for(register int j=1;j<=len[x];j++){A[i][j]=P[x][j];int y=x;while(y%A[i][j]==0) y/=A[i][j],K[i][j]++;}T[i]=len[x];}
for(register int i=1;i<n;i++){
int x=1,y=1,s=0;while(x<=T[i]&&y<=T[i+1]){
if(A[i][x]==A[i+1][y]){if((K[i][x]+K[i+1][y])&1) pp[++s]=A[i][x];x++,y++;}
else if(A[i][x]<A[i+1][y]){if(K[i][x]&1) pp[++s]=A[i][x];x++;} else{if(K[i+1][y]&1) pp[++s]=A[i+1][y];y++;}
}
while(x<=T[i]){if(K[i][x]&1) pp[++s]=A[i][x];x++;} while(y<=T[i+1]){if(K[i+1][y]&1) pp[++s]=A[i+1][y];y++;}
for(register int j=1;j<=s;j++) S[pp[j]][op[pp[j]]]+=(i-lst[pp[j]]),lst[pp[j]]=i,op[pp[j]]^=1;//,cout<<i<<' '<<pp[j]<<'\n';
}
// cout<<S[2][0]<<' '<<S[2][1]<<'\n';
for(register int i=1;i<=tot;i++) S[pri[i]][op[pri[i]]]+=n-lst[pri[i]],ans=1ll*ans*power(pri[i],min(S[pri[i]][0],S[pri[i]][1]))%p;cout<<ans<<'\n';return 0;
}
T2:
Description:
有一个 \(n×m\) 的棋盘。初始每个格子都是好的,之后每一秒会坏一个之前没坏的格子。\(nm\) 秒过后所有格子都会坏完。
我们想知道,每一秒过后,有多少子矩形满足其中的所有格子都是好的。
Input:
第一行两个整数 \(n,m\)。
接下来 \(nm\) 行,每行表示一个坏掉的格子。
数据保证每个格子只会坏一次。
Output:
输出 \(nm\) 行。第 \(i\) 行表示前 \(i\) 个格子坏掉后有多少子矩形是好的。
Sample1 Input:
2 2
1 1
2 1
1 2
2 2
Sample1 Output:
5
3
1
0
Hint:
对于 \(100\%\) 的数据,满足 \(1 \leq n,m \leq 500\)。
题目分析:
我们考虑坏一个格子,有多少个子矩形由好的变为坏的。我们维护一个 \(u_{i,j}\) 表示格子 \((i,j)\) 往上第一个坏格子的位置以及一个 \(d_{i,j}\) 表示格子 \((i,j)\) 往下第一个坏格子的位置。那么我们对于每个格子可以 \(O(m^2)\) 的暴力更新答案,由于跑不满故能通过此题(说不定能吊打标算
当然,正解和这个算法只差一步,我们仅需维护一个前缀和就能将复杂度优化到 \(O(n^2m)\)。
注意:我的代码对于 \(u_{i,j}\) 和 \(d_{i,j}\) 的定义略有不同,写的也是 \(O(nm^3)\) 的算法。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 505
#define LL long long
using namespace std;
int n,m,u[N][N],d[N][N],l[N][N],r[N][N];LL ans;
inline void solve(int x,int y){
for(register int i=y,u1=u[x][y],d1=d[x][y];i>=l[x][y];i--,u1=max(u1,u[x][i]),d1=min(d1,d[x][i]))
for(register int j=y,u2=u[x][y],d2=d[x][y];j<=r[x][y];j++,u2=max(u2,u[x][j]),d2=min(d2,d[x][j]))
ans-=1ll*(min(d1,d2)-x+1)*(x-max(u1,u2)+1);
for(register int i=y-1;i;i--) if(r[x][i]>=y) r[x][i]=y-1;else break;for(register int i=y+1;i<=m;i++) if(l[x][i]<=y) l[x][i]=y+1;else break;
for(register int i=x-1;i;i--) if(d[i][y]>=x) d[i][y]=x-1;else break;for(register int i=x+1;i<=n;i++) if(u[i][y]<=x) u[i][y]=x+1;else break;
}
inline int read(){int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;}
int main(){
n=read(),m=read(),ans=1ll*n*(n+1)/2ll*m*(m+1)/2ll;for(register int i=1;i<=n;i++) for(register int j=1;j<=m;j++) u[i][j]=1,d[i][j]=n,l[i][j]=1,r[i][j]=m;
for(register int i=1,x,y;i<=n*m;i++) x=read(),y=read(),solve(x,y),cout<<ans<<'\n';return 0;
}
T3:
Description:
有一个 \(2e9×2e9\) 的网格图,第 \(x\) 行第 \(y\) 列的格子的坐标为 \((x,y)\),也就是说左上角的格子的坐标为 \((1,1)\),右下角的坐标为 \((2e9,2e9)\)。
现在有个兄弟要从 \((x_1,y_1 )\) 走到 \((x_2,y_2)\),每次他只能走上下左右四个方向,这个兄弟永远不能走到网格图外面。
假设当前位置为 \((x,y)\),
向南走一步( \(x\) 加 \(1\))的代价为 \(2xy^2+2y^2+x^2\);
向北走一步( \(x\) 减 \(1\))的代价为 \(-2xy^2+2y^2+x^2\);
向东走一步( \(y\) 加 \(1\))的代价为 \(2x^2 y+2x^2+y^2\);
向西走一步( \(y\) 减 \(1\))的代价为 \(-2x^2 y+2x^2+y^2\);
请问从 \((x_1,y_1 )\) 走到 \((x_2,y_2 )\) 的最小代价是多少?
Input:
输入第一行一个正整数 \(n\) 表示数据组数。 接下来 \(n\) 行,每行四个整数 \(x_1,y_1,x_2,y_2\)。
Output:
对于每组数据,一行一个整数表示答案。请输出答案 mod \(998244353\)。
Sample1 Input:
4
1 1 1 1
1 3 2 1
2 1 1 3
10 2 20 6
Sample1 Output:
0
12
17
16999
Hint:
对于全部数据,\(1\leq n \leq 50000,1 \leq x1,y1,x2,y2 \leq 10^9\)
题目分析:
刚拿到这道题的时候说实话很难形成思路,但是我们可以先写个DP打个表,然后我们能发现一些有趣的结论。
我们强制让 \(x1\leq y1\) ,(可以通过交换 \(x1,y1\) 和 \(x2,y2\) 实现),于是可以大致分为4类:
1’.\(x1\leq x2\) 且 \(y1 \leq y2\) :
1‘’. \(x2 \leq y2\) 且 \(x2 \leq y1\) :我们采用 \(A->C->B\) 的行进路线:

2‘’. \(x2 \leq y2\) 且 \(x2 > y1\) :我们采用如下行进路线:
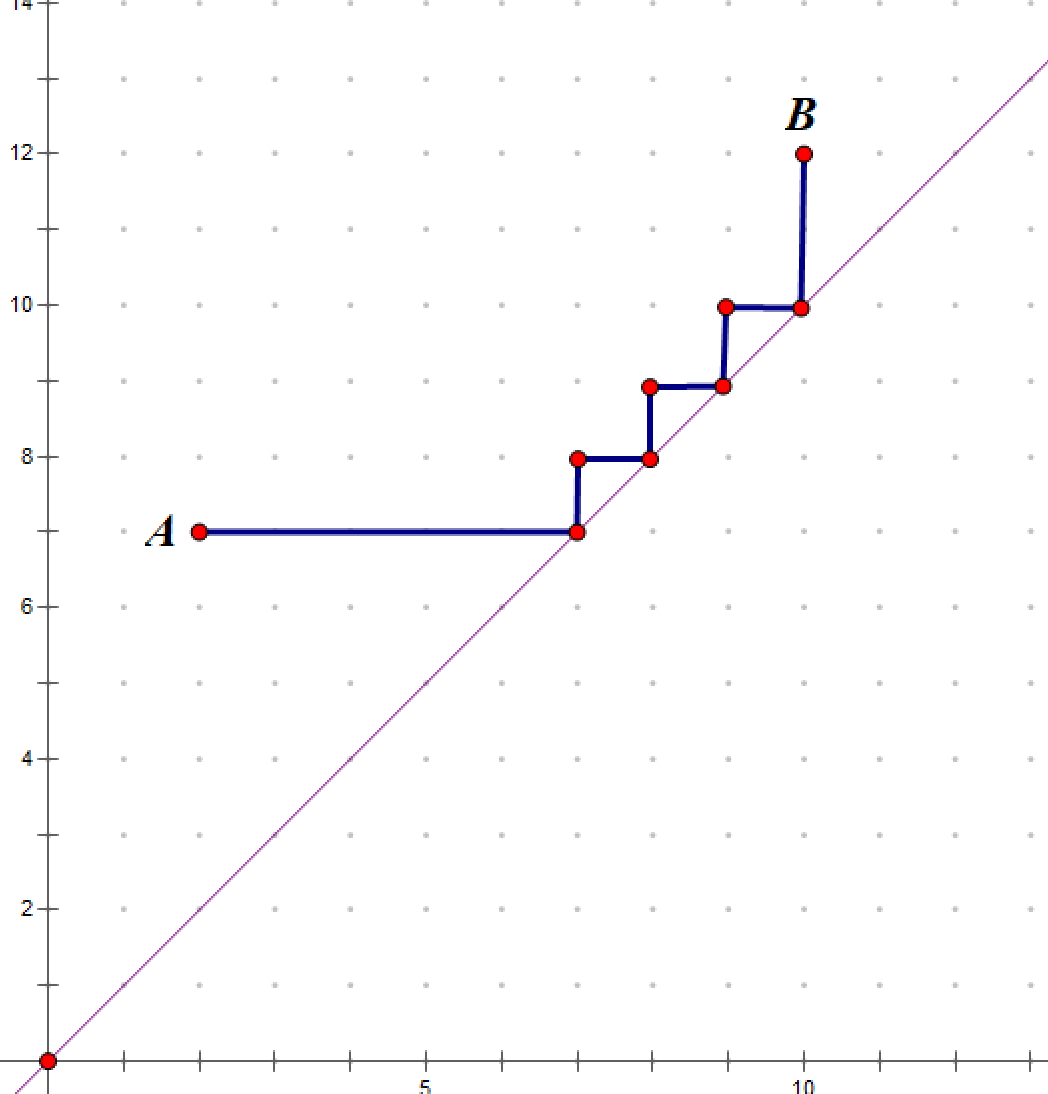
3‘’.\(x2>y2\):我们采用如下行进路线:
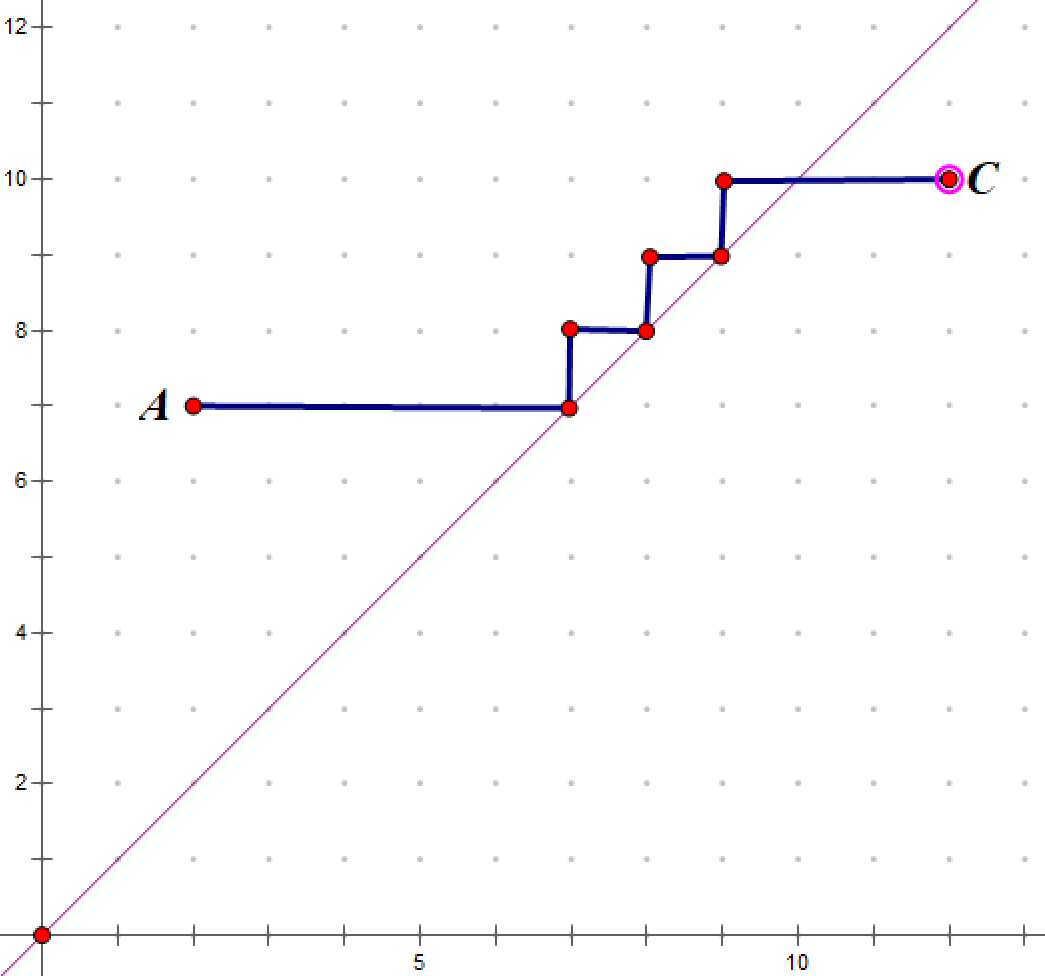
2‘.\(x1>x2\) 且 \(y1\le y2\):我们采用如下行进路线:

3’.\(x1\le x2\) 且 \(y1>y2\):我们采用如下行进路线:
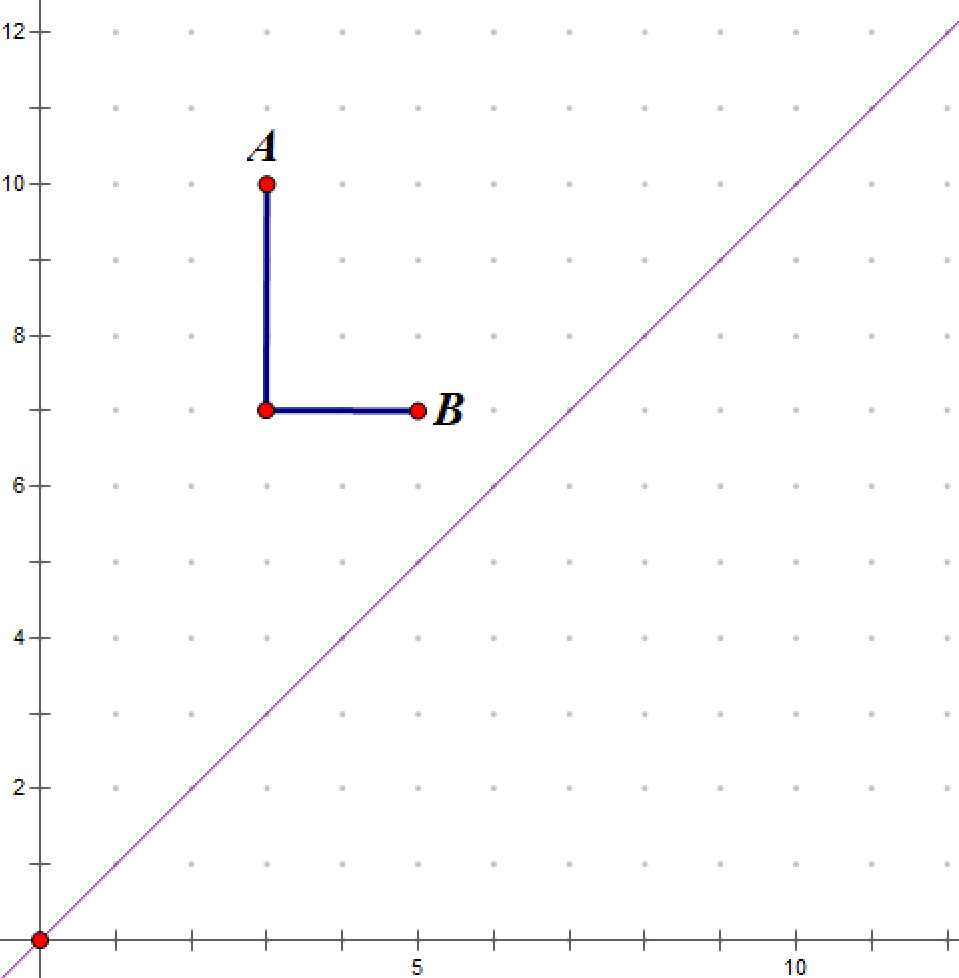
4‘.\(x1>x2\) 且 \(y1>y2\):
1’‘.\(x2\leq y2\) 且 \(x1\leq y2\):我们采用如下行进路线:
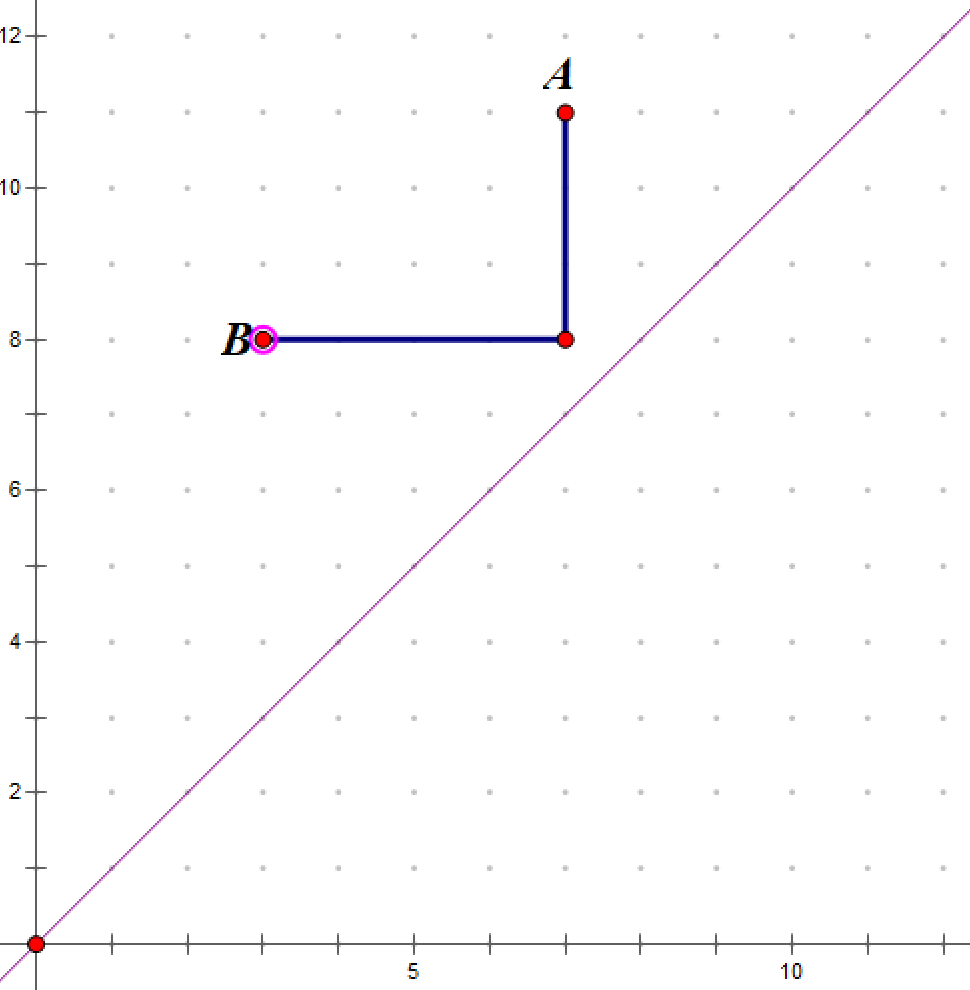
2’‘.\(x2\leq y2\) 且 \(x1>y2\):我们采用如下行进路线:
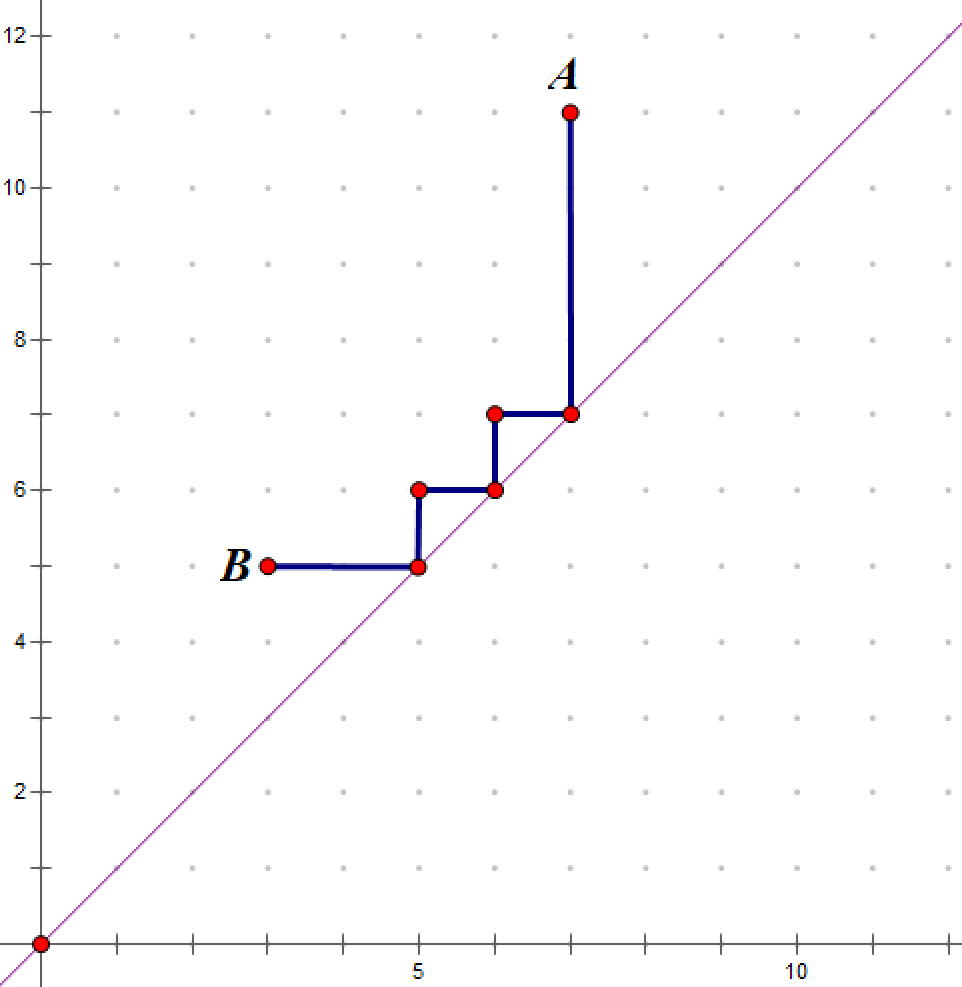
3’‘.\(x2>y2\):我们采用如下行进路线:
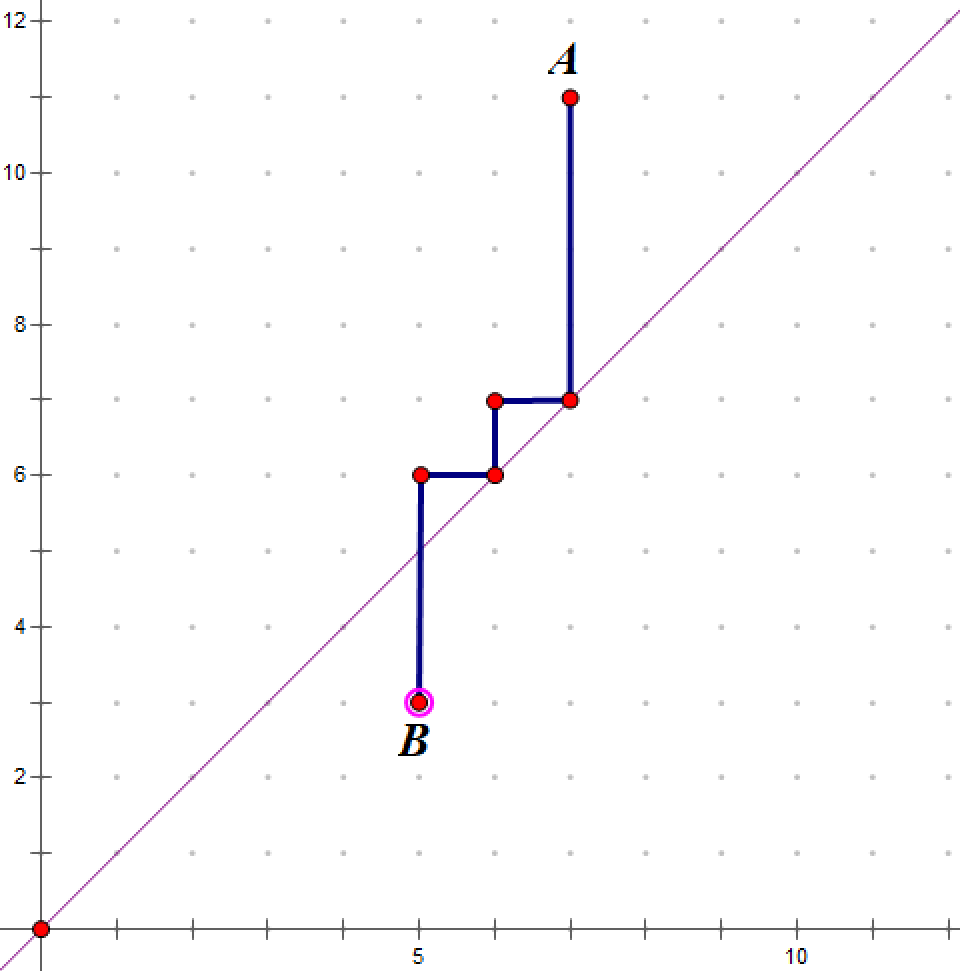
知道路线怎么走之后我们就能“轻松”地打出这道题,但是问题在于为什么路线是这样走的呢?
我们观察代价的柿子就会发现,一条路径 \((x_1,y_1)->(x_2,y_2)->……->(x_n,y_n)\) 的代价为 \(x_n^2y_n^2-x_1^2y_1^2+\sum_{i=1}^{n-1}{(x_i^2+y_i^2)}\)
由此看来,我们的代价只与 \(\sum_{i=1}^{n-1}{(x_i^2+y_i^2)}\) 有关,用贪心和基本不等式的思想稍微想一想就能粗略证明上述分类讨论的正确性。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 2000005
#define LL long long
using namespace std;
int T,inv;const int p=998244353;
inline int power(int x,int y){int z=1;while(y){if(y&1) z=1ll*z*x%p;y>>=1,x=1ll*x*x%p;}return z;}
inline int calc1(int x,int y){return (1ll*(x+y)*(y-x+1)/2ll)%p;}
inline int calc2(int x,int y){return (1ll*y*(y+1)%p*(2*y+1)%p*inv%p-1ll*(x-1)*x%p*(2*x-1)%p*inv%p+p)%p;}
inline int calc3(int x,int y){return (1ll*calc1(1,y)*calc1(1,y)%p-1ll*calc1(1,x-1)*calc1(1,x-1)%p+p)%p;}
inline int read(){int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;}
int main(){
inv=power(6,p-2),T=read();while(T--){
int sx=read(),sy=read(),tx=read(),ty=read();if(sx>sy) swap(sx,sy),swap(tx,ty);
if(sx<=tx&&sy<=ty){
if(tx<=ty){
if(sy>=tx){
LL res1=(2ll*calc1(sx,tx-1)*sy%p*sy%p+2ll*sy*sy%p*(tx-sx)%p+(LL)calc2(sx,tx-1))%p;
LL res2=(2ll*calc1(sy,ty-1)*tx%p*tx%p+2ll*tx*tx%p*(ty-sy)%p+(LL)calc2(sy,ty-1))%p;
LL ans=(res1+res2)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
else{
LL res1=(2ll*calc1(sx,sy-1)*sy%p*sy%p+2ll*sy*sy%p*(sy-sx)%p+(LL)calc2(sx,sy-1))%p;
LL res2=(2ll*calc3(sy,tx-1)+2ll*calc3(sy+1,tx)+4ll*calc2(sy,tx-1))%p;
LL res3=(2ll*calc1(tx,ty-1)*tx%p*tx%p+2ll*tx*tx%p*(ty-tx)%p+(LL)calc2(tx,ty-1))%p;
LL ans=(res1+res2+res3)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
}
else{
LL res1=(2ll*calc1(sx,sy-1)*sy%p*sy%p+2ll*sy*sy%p*(sy-sx)%p+(LL)calc2(sx,sy-1))%p;
LL res2=(2ll*calc3(sy,ty-1)+2ll*calc3(sy+1,ty)+4ll*calc2(sy,ty-1))%p;
LL res3=(2ll*calc1(ty,tx-1)*ty%p*ty%p+2ll*ty*ty%p*(tx-ty)%p+(LL)calc2(ty,tx-1))%p;
LL ans=(res1+res2+res3)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
}
if(sx>tx&&sy<=ty){
LL res1=(-2ll*calc1(tx+1,sx)*sy%p*sy%p+2ll*sy*sy%p*(sx-tx)%p+(LL)calc2(tx+1,sx))%p;
LL res2=(2ll*calc1(sy,ty-1)*tx%p*tx%p+2ll*tx*tx%p*(ty-sy)%p+(LL)calc2(sy,ty-1))%p;
LL ans=(res1+res2)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
if(sx<=tx&&sy>ty){
LL res1=(-2ll*calc1(ty+1,sy)*sx%p*sx%p+2ll*sx*sx%p*(sy-ty)%p+(LL)calc2(ty+1,sy))%p;
LL res2=(2ll*calc1(sx,tx-1)*ty%p*ty%p+2ll*ty*ty%p*(tx-sx)%p+(LL)calc2(sx,tx-1))%p;
LL ans=(res1+res2)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
if(sx>tx&&sy>ty){
if(tx<=ty){
if(ty>=sx){
LL res1=(-2ll*calc1(ty+1,sy)*sx%p*sx%p+2ll*sx*sx%p*(sy-ty)%p+(LL)calc2(ty+1,sy))%p;
LL res2=(-2ll*calc1(tx+1,sx)*ty%p*ty%p+2ll*ty*ty%p*(sx-tx)%p+(LL)calc2(tx+1,sx))%p;
LL ans=(res1+res2)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
else{
LL res1=(-2ll*calc1(sx+1,sy)*sx%p*sx%p+2ll*sx*sx%p*(sy-sx)%p+(LL)calc2(sx+1,sy))%p;
LL res2=(-2ll*calc3(ty+1,sx)-2ll*calc3(ty,sx-1)+4ll*calc2(ty+1,sx))%p;
LL res3=(-2ll*calc1(tx+1,ty)*ty%p*ty%p+2ll*ty*ty%p*(ty-tx)%p+(LL)calc2(tx+1,ty))%p;
LL ans=(res1+res2+res3)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
}
else{
LL res1=(-2ll*calc1(sx+1,sy)*sx%p*sx%p+2ll*sx*sx%p*(sy-sx)%p+(LL)calc2(sx+1,sy))%p;
LL res2=(-2ll*calc3(tx+1,sx)-2ll*calc3(tx,sx-1)+4ll*calc2(tx+1,sx))%p;
LL res3=(-2ll*calc1(ty+1,tx)*tx%p*tx%p+2ll*tx*tx%p*(tx-ty)%p+(LL)calc2(ty+1,tx))%p;
LL ans=(res1+res2+res3)%p;ans=(ans+p)%p;cout<<ans<<'\n';continue;
}
}
}
return 0;
}
//向南走一步(x+1)的代价为 2xy^2+2y^2+x^2;
//向北走一步(x-1)的代价为 -2xy^2+2y^2+x^2;
//向东走一步(y+1)的代价为 2x^2y+2x^2+y^2;
//向西走一步(y-1)的代价为 -2x^2y+2x^2+y^2;
T4:
Description:
今天是杜老师的生日,蜗蜗给杜老师买了个大蛋糕。蛋糕里一共有 \(n\) 块巧克力,巧克力的形状都是长方体,第 \(i\) 块巧克力包含了所有点 \((x,y,z)\) 满足 \(minx[i]≤x≤maxx[i],miny[i]≤y≤maxy[i],minz[i]≤z≤maxz[i]\) 。巧克力之间可能会有重叠。
杜老师想在上面切三刀。第一刀必须切一个 \(x=a\) 的平面,第二刀必须切一个 \(y=b\) 的平面,第三刀必须切一个 \(z=c\) 的平面,其中 \(a,b,c\) 为 \(3\) 个整数。与此同时,需要满足每一块巧克力都至少被其中一刀切到(切到的定义是巧克力和至少一个平面的交非空)。
请帮杜老师切这 \(3\) 刀。
Input:
第一行一个整数 \(n\)。 接下来 \(n\) 行,每行 \(6\) 个整数 \(minx[i],maxx[i],miny[i],maxy[i],minz[i],maxz[i]\)。
Output:
如果无解,输出NO。
否则第一行输出YES,第二行输出 \(3\) 个整数 \(a,b,c\)
如果存在多解,输出任意一组即可。
Sample1 Input:
3
0 1 0 1 0 1
10 11 10 11 10 11
999999999 1000000000 999999999 1000000000 999999999 1000000000
Sample1 Output:
YES
0 10 999999999
Sample2 Input:
4
0 1 0 1 0 1
999999999 1000000000 0 1 0 1
0 1 999999999 1000000000 0 1
0 1 0 1 999999999 1000000000
Sample2 Output:
YES
0 0 0
Hint:
对于 \(100\%\) 的数据,满足 \(1\le n\le 10^5\),\(-10^9\le minx[i],maxx[i],miny[i],maxy[i],minz[i],maxz[i]\le 10^9\),\(minx[i]<maxx[i],miny[i]<maxy[i],minz[i]<maxz[i]\)。
题目分析:
正解貌似是线段树,但是码量太大了,博主目前还没有写正解的打算(我太菜了
于是博主讲一讲博主的骗分方法。我们对于每一个 \(x=i\) 预处理出能切到的蛋糕数量。按照数量从大到小排序,然后用 \(nlogn\) 的复杂度对于每一个 \(x=i\) 判断一遍,知道找出合法解。如果超过时间限制就直接退出输出“NO”。根据实测可以拿到 \(80\) 分。
我们把时限分成三份,分别对 \(x,y,z\) 都做一遍。该方法通过实测可以拿到 \(90\) 分...
Hack 数据造起来不是很难,但是在考场上拿分还是能拿到可观的分数,由此可见骗分的重要性。
80分代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 100005
#define inf 1000000001
#define max(a,b) (a)>(b)?(a):(b)
#define s_id multiset<int>::iterator
using namespace std;
int n,m,tot,R[N],V[N],rk[N],lx[N],rx[N],ly[N],ry[N],lz[N],rz[N],p[N],S[N*6];multiset<int> T1,T2;vector<int> g;
struct node{int ly,ry,lz,rz;bool operator <(const node&x)const{return ry>x.ry;}};priority_queue<node> heap;
inline bool cmp(int x,int y){return ly[x]<ly[y];}
inline bool cmp2(int x,int y){return V[x]>V[y];}
inline int get(int x){return lower_bound(g.begin(),g.end(),x)-g.begin()+1;}
inline void U(int x,int y){for(register int i=x;i<=m;i+=i&-i) S[i]+=y;}
inline int Q(int x){int res=0;for(register int i=x;i;i-=i&-i) res+=S[i];return res;}
inline void solve(int X){
if(!tot){puts("YES");cout<<g[X-1]<<" 0 0"<<'\n';exit(0);} T1.clear(),T2.clear();for(register int i=1;i<=tot;i++) T1.insert(lz[p[i]]),T2.insert(rz[p[i]]);
s_id it=T1.end();it--;int maxz=*it,minz=*T2.begin();if(minz>=maxz){puts("YES");cout<<g[X-1]<<" 0 "<<g[maxz-1]<<'\n';exit(0);}
while(!heap.empty()) heap.pop();for(register int i=1;i<=tot;i++){
int Y=ly[p[i]];while(!heap.empty()){node tmp=heap.top();if(tmp.ry<Y) heap.pop(),T1.insert(tmp.lz),T2.insert(tmp.rz);else break;}
it=T1.lower_bound(lz[p[i]]);T1.erase(it);it=T2.lower_bound(rz[p[i]]);T2.erase(it);heap.push(node{ly[p[i]],ry[p[i]],lz[p[i]],rz[p[i]]});
if(T1.empty()){puts("YES");cout<<g[X-1]<<' '<<g[Y-1]<<" 0"<<'\n';exit(0);}it=T1.end();it--,maxz=*it,minz=*T2.begin();
if(minz>=maxz){puts("YES");cout<<g[X-1]<<' '<<g[Y-1]<<' '<<g[maxz-1]<<'\n';exit(0);}
}
}
inline int read(){int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;}
int main(){
n=read();for(register int i=1;i<=n;i++) R[i]=i,lx[i]=read(),rx[i]=read(),ly[i]=read(),ry[i]=read(),lz[i]=read(),rz[i]=read(),rk[i]=i,
g.push_back(lx[i]),g.push_back(rx[i]),g.push_back(ly[i]),g.push_back(ry[i]),g.push_back(lz[i]),g.push_back(rz[i]);
sort(g.begin(),g.end()),g.erase(unique(g.begin(),g.end()),g.end()),sort(rk+1,rk+n+1,cmp),m=g.size();for(register int i=1;i<=n;i++)
lx[i]=get(lx[i]),ly[i]=get(ly[i]),lz[i]=get(lz[i]),rx[i]=get(rx[i]),ry[i]=get(ry[i]),rz[i]=get(rz[i]),U(lx[i],1),U(rx[i]+1,-1);for(register int i=1;i<=n;i++) V[i]=Q(lx[i]);sort(R+1,R+n+1,cmp2);
for(register int i=1;i<=n;i++){if((double)clock()/CLOCKS_PER_SEC>2.5){break;}int X=lx[R[i]];tot=0;for(register int j=1;j<=n;j++) if(lx[rk[j]]>X||X>rx[rk[j]]) p[++tot]=rk[j];solve(X);}puts("NO");return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号