树状数组 学习笔记

树状数组

P3374 【模板】树状数组 1
网址：https://www.luogu.com.cn/problem/P3374
题目描述
如题，已知一个数列，你需要进行下面两种操作：
• 将某一个数加上 xx
• 求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,mn,m，分别表示该数列数字的个数和操作的总个数。
第二行包含 nn 个用空格分隔的整数，其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 mm 行每行包含 33 个整数，表示一个操作，具体如下：
• 1 x k 含义：将第 xx 个数加上 kk
• 2 x y 含义：输出区间 [x,y][x,y] 内每个数的和
输出格式
输出包含若干行整数，即为所有操作的结果。
输入输出样例
输入 复制
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 复制
14
16
说明/提示
【数据范围】
对于 30%30% 的数据，1 \le n \le 81≤n≤8，1\le m \le 101≤m≤10；
对于 70%70% 的数据，1\le n,m \le 10^41≤n,m≤104；
对于 100%100% 的数据，1\le n,m \le 5\times 10^51≤n,m≤5×105。
样例说明：
故输出结果14、16

一道树状数组的经典原题。
其实，也可以用暴力，但是，如果TLE别怪我~~~~~~

首先，开一个数组，维护数组a的值，具体如图：

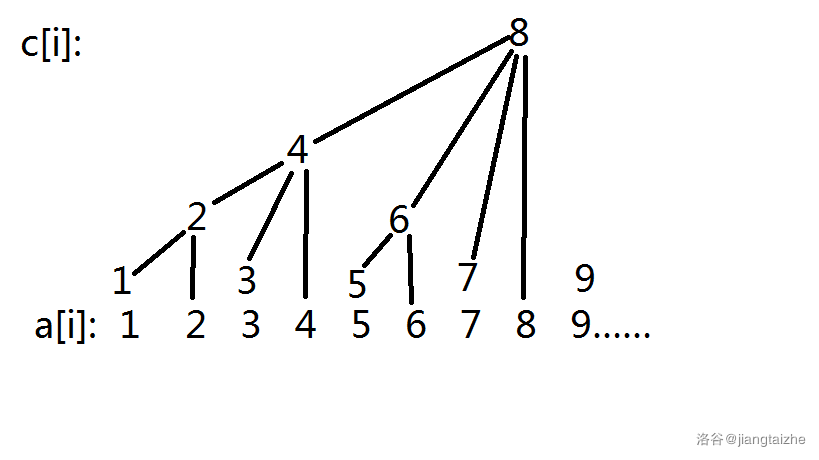
这样，每一个数的父亲就相当于他的二进制的最低位 +他自己；
反过来，一个根节点的儿子就是他减去他的二进制的最低位；

然而，利用负数的补码，可以完成这个常数超级小的方法：
cpp int lowbit(int x){ return x&-x; }
稍微理解一下，就OK了。

代码君献上代码：（AC代码）

#include<bits/stdc++.h>//luogu P3374
#define maxn 500001
using namespace std;
int a[maxn],c[maxn];
int x,y,n,T,k;
int lowbit(int x){ return x&-x; }//核心
int find(int x){//查找
	int s=0;
	while(x>0){
		s+=c[x];
		x-=lowbit(x);
	}
	return s;
}
void update(int x,int v){//修改
	while(x<=n){
		c[x]+=v;
		x+=lowbit(x);
	}
}
int main(){
	scanf("%d%d",&n,&T);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		update(i,a[i]);
	}
	    
	while(T--){
		scanf("%d",&k);
		if(k==1){//修改 
			scanf("%d%d",&x,&y);
			update(x,y);
		}
		else{//查询 
			scanf("%d%d",&x,&y);
			printf("%d\n",find(y)-find(x-1));
		}
	}
}```