matlab PCA分析

pca( )

采用matlab自带的函数pca()进行主成分分析

[coeff, score, latent, tsquared, explained, mu] = pca(x)

假设数据x为n行p列的多变量数据，n为观测次数，p为变量维度。

coeff：为PCA变换系数，也称为loadings。

score：为PCA变换后的主成分（潜变量）。

latent：这里指的是各个主成分解释的方差。

tsquared：Hotelling's T-squared统计量（等价于潜变量的马氏平方距离，即mahal(score,score)）

explained：指的是每个主成分解释的方差所占百分比。

mu：x中每列（每个变量）的均值。

 

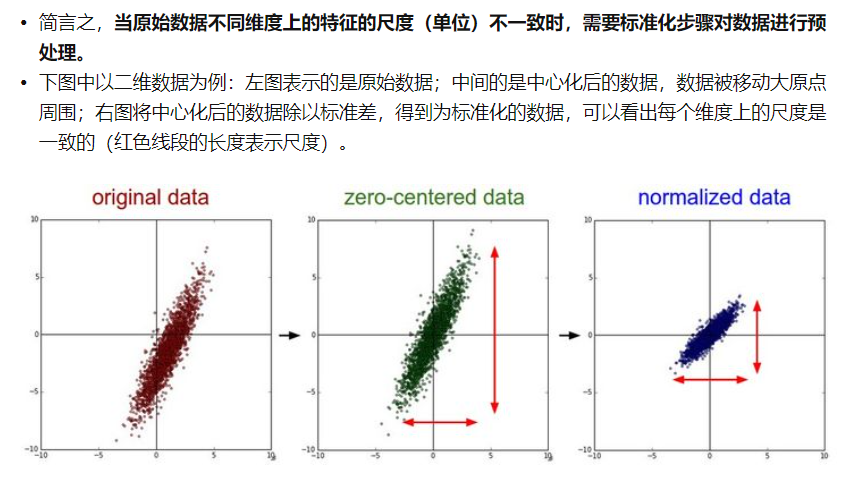
需要注意：matlab中的PCA函数会自动对输入数据做去均值处理（X-mu），并返回均值mu。但是默认不进行标准化处理，即（X-mu）/sigma。因此，如果X的各维度特征尺度差异较大，则应先对X进行标准化处理。通过标准化进行无量纲处理，使得各维度特征尺度一致。

https://www.zhihu.com/question/37069477

 

## 进行标准化训练和测试

% 模型训练
[z, mu, sigma] = zscore(X); % 求训练集的均值mu和标准差sigma

[coeff,score,latent,tsquared,explained,~] = pca(z);

% 模型测试
Y = (Y - mu)./sigma;  % 测试数据标准化处理
score_test = Y/coeff'; % PCA变换

## 仅去中心化（x-mu）（默认）

% 模型训练
[coeff,score,latent,tsquared,explained,mu] = pca(X);

% 模型测试
score_test = (Y-mu)/coeff'; % PCA变换

　　

示例

假设x具有6个变量。

coeff

coeff =

0.3523 -0.1291 0.2885 0.1351 0.6760 -0.5483
0.3405 0.5773 0.6790 -0.0005 -0.2867 0.0865
0.2557 -0.2643 0.1687 -0.0672 0.4160 0.8116
0.4491 -0.3097 -0.1197 0.7441 -0.3653 0.0314
0.5791 0.4562 -0.6329 -0.2062 0.1145 0.0220
0.3969 -0.5255 0.1114 -0.6173 -0.3757 -0.1779

latent =

0.0024
0.0003
0.0002
0.0001
0.0000
0.0000

explained =

80.4144
10.1631
5.5321
2.2133
1.2835
0.3936

mu =

0.0469 0.0407 0.0355 0.0596 0.0614 0.0486

（1）检查主成分score

图1 各主成分的分布

 

(2) 重构

% 重构（减去均值后的数据）
Xcentered = score*coeff'; 

 

 注意pca系数要转置，重构结果是x减去均值mu后的值。

图2 重构结果

 

(3)  仅保留前n个主成分

% 仅取前n个主成分（T2依然是6个主成分的值）
NumComponents = 1;
[coeff,score,latent,tsquared,explained,mu] = pca(RL2_mean, 'NumComponents', NumComponents);

注意返回的T2依然是6个主成分的值。

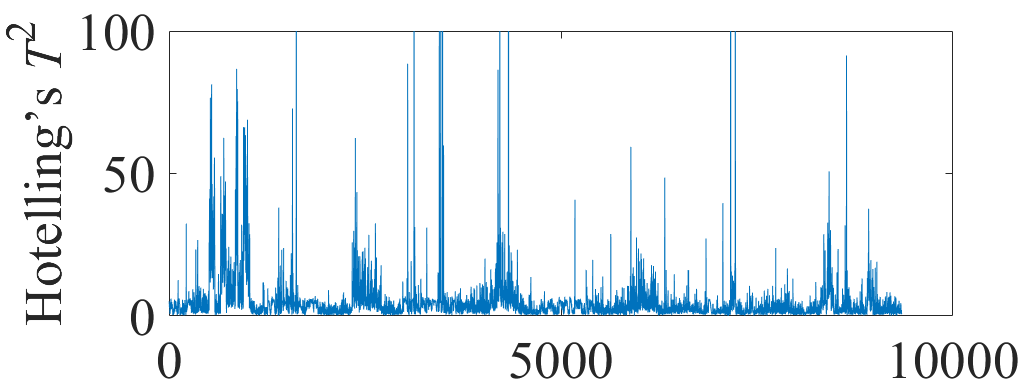
图3 T2统计量

可以计算保留的主成分空间和残差主成分空间的T2统计量

% 保留主成分空间的T2（其实就是马氏平方距离）
tsqreduced = mahal(score,score);
% 残差主成分空间的T2
tsqdiscarded = tsquared - tsqreduced;

图4 主成分空间T2统计量

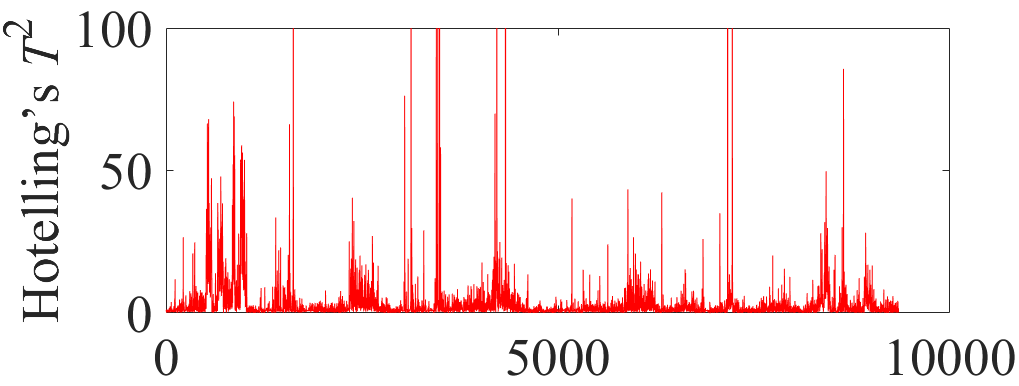
图5 残差主成分空间T2统计量

(4) 加权PCA

这里通过方差加权后结果会略有变化。

Use the inverse variable variances as weights while performing the principal components analysis.

在进行主成分分析时，使用变量方差的逆作为权重。

% 注意这里wcoeff并不正交
[wcoeff,~,latent,~,explained, mu] = pca(RL2(1:9344, :), 'VariableWeights','variance');

% 正交系数矩阵
coefforth = inv(diag(std(RL2(1:9344, :))))*wcoeff;

% 测试集
score_test_w = (RL2-mu)/coefforth';

% 全部主成分的T2统计量（其实就是马氏平方距离）
tsquared = mahal(score_test_w, score_test_w);
% 第一主成分的T2统计量(越靠前的主成分对T2的幅值贡献越小)
tsqreduced = mahal(score_test_w(:, 1),score_test_w(:, 1));
% 残余主成分空间的T2统计量（可以直接相减）
tsqdiscarded = tsquared - tsqreduced;