❗❗142环形链表II

力扣刷题 142.环形链表 II-- day4

题目分析

这道题目难度较大， 特别是要求空间复杂度为 O(1)的时候

如果不追求空间复杂度的话， 可以使用 hash 表

把目前遍历的节点指针存入 hash 表， 当下次在 hash 表中找到该节点时， 即找到了答案

空间复杂度为 O（1）的解法：
较为复杂， 具有一定的数学分析
下次再实现

解法一、使用 unordered_set 作为 hash 表

ListNode *detectCycle(ListNode *head)
{
    unordered_set<ListNode *> nodeSet;
    while (head)
    {
        if (nodeSet.find(head) != nodeSet.end())
        {
            return head;
        }
        else
        {
            nodeSet.insert(head);
            head = head->next;
        }
    }
    return nullptr;
}

解法二、使用快慢指针

分析如下:

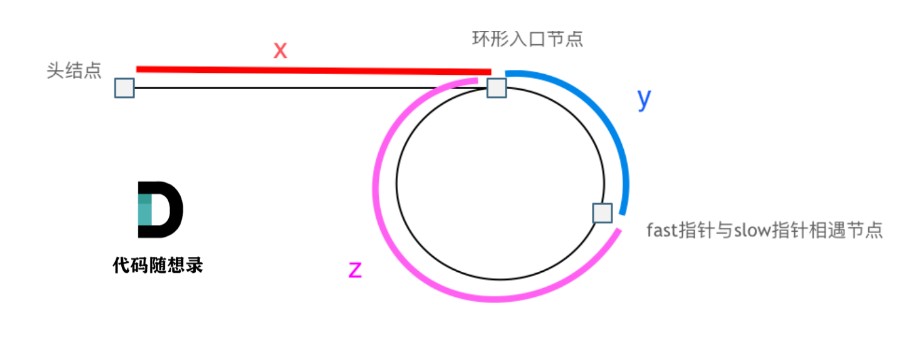
慢指针一次走一步， 快指针走两步， 如果链表有环， 则快指针必定会追上满指针（相对速度为 1），假设相遇点在 y 处。

可以证明慢指针走第一圈的时候， 两者就相遇了:
设环的长度为 L，慢指针刚到环起始点时， 快指针在某个位置
无论如何， 快指针与满指针最多相隔 L-1， 也就是快指针刚好在慢指针前面一个位置， 这时快指针追上慢指针的时间最长为（L - 1）, 小于慢指针走一圈的时间

接下来， 就可以推导公式：
慢指针走的路程: x + y = s1
快指针走的路程: x + y + n(y+z) = s2//多走了 n 圈
由两倍关系: s12 = s2

得出: x = z + (n-1)(y+z) = z + (n-1)L

利用这个关系如何得到环形链表的入口节点呢？
在头结点和相遇节点分别放一个指针， 向前移动直至相遇
相遇的节点即为入口节点

最终代码:

ListNode *detectCycle(ListNode *head)
{
    ListNode *slow = head, *fast = head;

    while (fast)
    {
        slow = slow->next;
        if (!fast->next)
        {
            break;
        }
        fast = fast->next->next;
        if (slow == fast)
        {
            ListNode *temp = head;
            while (temp != slow)
            {
                temp = temp->next;
                slow = slow->next;
            }
            return temp;
        }
    }
    return nullptr;
}