【集体智慧编程】第五章 优化

目录¶ 

• 介绍
• 在实践中学习：组团旅游
  • 描述题解（将问题转化为数学表示）
  • 成本函数
  • 最优组合（找出让成本函数最低的组合）
    • 随机搜索
    • 爬山法
    • 模拟退火算法
    • 遗传算法
  • 真实案例
• 优化的其它应用
  • 涉及偏好的优化（学生宿舍分配问题）
  • 网络可视化（数据可视化）

介绍¶

优化技术主要用于处理：受多种变量影响、存在多种可能解的问题（无法一一尝试）、结果因变量组合不同而产生很大变化的问题。如

• 物理学：分子运动
• 生物学：预测蛋白质结构
• 计算机科学：预测算法的最坏可能运行时间

本文旨在解决三个问题

• 如何制定组团旅游计划？
• 如何基于人们的偏好来分配有限的资源？
• 如何用最少的交叉线来可视化社会网络？

组团旅游¶

数据介绍¶

6个人在不同地方，决定一起到LGA旅游。他们将在同一天到达，并在同一天离开。

import time
import random
import math

people = [('Seymour','BOS'),
          ('Franny','DAL'),
          ('Zooey','CAK'),
          ('Walt','MIA'),
          ('Buddy','ORD'),
          ('Les','OMA')]
# Laguardia
destination='LGA'

航班信息存储在schedule.txt，数据格式为：起点、终点、起飞时间、到达时间、价格。
将数据载入字典，以起止点为键，航班详细信息为值。

flights = {}
for line in open("schedule.txt"):
    origin, dest, depart, arrive, price = line.strip().split(',')
    flights.setdefault((origin,dest), [])
    
    #将航班信息加入字典
    flights[(origin, dest)].append((depart, arrive, int(price)))
    
    #计算给定时间在一天中的分钟数
    def getminutes(t):
        x = time.strptime(t,'%H:%M')
        return x[3]*60 + x[4]

描述题解¶

数字序列：一个数字代表某人选择乘坐的航班（0是第一次航班，1是第二次航班）
例如: [1,4,3,2,7,3,6,3,2,4,5,3]
将list转化成可读的形式

def printschedule(r):
    for d in range(int(len(r)/2)):
        name = people[d][0]
        origin = people[d][1]
        out = flights[(origin,destination)][int(r[2*d])]
        ret = flights[(destination,origin)][int(r[2*d+1])]
        print('%10s%10s %5s-%5s $%3s %5s-%5s $%3s' % (name,origin,
                                                  out[0],out[1],out[2],
                                                  ret[0],ret[1],ret[2]))
s = [1,4,3,2,7,3,6,3,2,4,5,3]
printschedule(s)

运行结果如图：

 

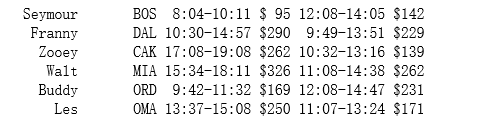
成本函数¶

成本算法是优化算法解决问题的关键，即优化算法的目标，就是寻找一组使成本函数的返回结果达到最小的输入。因组成本函数需要返回一个值来表示方案的好坏（一般数值越大，表示方案越差）
成本函数的构建需要明确最重要的变量

本例中，输入为航班信息，成本函数需要考虑的变量可以是：价格、旅行时间（在飞机上的时间）、等待时间（在机场等待其它成员达到的时间）、汽车租用时间（如果集体租用一辆汽车，需要在一天内早于起租时间归还，否则将多付一天的租金）
本例中使用的变量包括：

- 总的旅行成本
- 在机场互相等待时间
- 如果汽车是在租用时间点后归还，需多支付$50的罚款

def schedulecost(sol):
    totalprice = 0
    latestarrival = 0  #最晚到达
    earliestdep = 24*60 #最早离开
    
    for d in range(int(len(sol)/2)):
        #得到往程和返程航班
        origin = people[d][1]
        outbound = flights[(origin, destination)][int(sol[2*d])] #只要一部分信息就可以查到
        returnf  = flights[(destination,origin)][int(sol[2*d+1])]
        #总价格
        totalprice += outbound[2]
        totalprice += returnf[2]
        #记录最晚到达和最早离开的时间
        #将每个航班的到达时间进行比较，得到最晚到达的时间
        if latestarrival < getminutes(outbound[1]): latestarrival = getminutes(outbound[1])
         #将每个航班的离开时间进行比较，得到最早离开的时间
        if earliestdep > getminutes(returnf[0]): earliestdep = getminutes(returnf[0])
    #往程时，每个人需要在机场等待大家都到了后一起去酒店
    #返程时，大家一起租车到机场，然后各自等待自己的航班
    totalwait = 0
    for d in range(int(len(sol)/2)):
        origin = people[d][1]
        outbound = flights[(origin, destination)][int(sol[2*d])]
        returnf  = flights[(destination,origin)][int(sol[2*d+1])]
        totalwait += latestarrival-getminutes(outbound[1])
        totalwait += getminutes(returnf[0])-earliestdep
    #是否要多付一天的汽车租用费用？
    if latestarrival < earliestdep: totalprice += 50
    return totalprice # totalwait

最优组合（随机算法）¶

这个函数接受两个参数

• domain是一个 2-tuple 构成的列表，指定了每个变量的最小值和最大值
• costf，即成本函数

该函数会随机产生1000次猜测，并对每一猜测调用costf，最后返回具有最低成本的题解

def randomoptimize(domain, costf):
    best = 999999999
    bestr=None
    for i in range(0,1000):
        #创建随机解
        r = [float(random.randint(domain[i][0],domain[i][1])) for i in range(len(domain))]
    
        #成本
        cost = costf(r)
        
        #与目前得到的最优解进行比较
        if cost < best:
            best  = cost
            bestr = r
    return r

domain = [(0,9)]*(len(people)*2)
s = randomoptimize(domain, schedulecost)
print(schedulecost(s))
print(printschedule(s))

运行结果如下：

 

 

1000次猜测在全部可能性中仅占非常小的一部分，但在本例中仍可找出不少表现尚可（不一定是最优）的解。
由于是随机的原因，每次运行得到的结果可能不同。可以多执行几次，看看成本值变化是否很大，或者增大循环次数。

 

最优组合（爬山法）¶

随机算法的缺点：低效
本例特点：拥有较低成本的时间安排很可能接近其它低成本安排。而随机算法是到处跳跃的，不会自动寻找已被发现的优解相接近的解。
爬山法：从一个随机解开始，然后在其临近的解集中寻找更好的题解（具有更低的成本） 在本例中，先确定一个随机安排让所有人都能出发，对每一个相邻时间安排进行成本计算，最低成本的安排成为新题的解。 优点：速度快 缺陷：可能得到局部范围最小值而不是全局最小值 解决方法

- 随机重复爬山法：多个随机生成的初始解作为起点运行若干次，借此希望其中有一个能逼近全局最小值。
- 模拟退火算法
- 遗传算法

def hillclimb(domain, costf):
    #创建一个随机解
    sol = [random.randint(domain[i][0], domain[i][1]) for i in range(len(domain))]
    #主循环
    while 1:
        neighbors = []
        for j in range(len(domain)):
            #在每个方向上相对于原值偏离一点（+1或者-1，偏离一个单位距离）
            if sol[j] > domain[j][0]:
                neighbors.append(sol[0:j]+[sol[j]+1]+sol[j+1:])
            if sol[j]<domain[j][1]:
                neighbors.append(sol[0:j]+[sol[j]-1]+sol[j+1:])
    #在相邻解中寻找最优解
    current = costf(sol)
    best = current
    for j in range(len(neighbors)):
        cost = costf(neighbors[j])
        if cost < best:
            best = cost
            sol = neighbors[j]

        # 如果没有更好的解，退出循环
        if best == current:
            break
    return sol

 

to be continue