快速傅里叶变换

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

计算量小的显著的优点，使得FFT在信号处理技术领域获得了广泛应用，结合高速硬件就能实现对信号的实时处理。例如，对语音信号的分析和合成，对通信系统中实现全数字化的时分制与频分制(TDM/FDM)的复用转换，在频域对信号滤波以及相关分析，通过对雷达、声纳、振动信号的频谱分析以提高对目标的搜索和跟踪的分辨率等等，都要用到FFT。可以说FFT的出现，对数字信号处理学科的发展起了重要的作用。

https://zhuanlan.zhihu.com/p/31584464

傅里叶变换

快速傅里叶变换（Fast Fourier Transform，FFT）是一种可在

时间内完成的离散傅里叶变换（Discrete Fourier transform，DFT）算法。

在算法竞赛中的运用主要是用来加速多项式的乘法。

考虑到两个多项式

的乘积

，假设

的项数为

，其系数构成的

维向量为

，

的项数为

，其系数构成的

维向量为

。

我们要求

的系数构成的

维的向量，先考虑朴素做法。

可以用这段代码表示：

for ( int i = 0 ; i < n ; ++ i )
	for ( int j = 0 ; j < m ; ++ j )  {
		c [i + j] += a [i] * b [j] ;
	}

思路非常清晰，其时间复杂度是

的。

所以我们来学习快速傅里叶变换。

0x01 关于多项式

多项式有两种表示方法，系数表达法与点值表达法

多项式的系数表示法

设多项式

为一个

次的多项式，显然，所有项的系数组成的系数向量

唯一确定了这个多项式。

多项式的点值表示法

将一组互不相同的

（叫插值节点）分别带入

，得到

个取值

其中

定理:

一个

次多项式在

个不同点的取值唯一确定了该多项式。

证明：

假设命题不成立，存在两个不同的

次多项式

，满足对于任何

，有

。
令

，则

也是一个

次多项式。对于任何

，都有

。
即

有

个根，这与代数基本定理（一个

次多项式在复数域上有且仅有

个根）相矛盾，故

并不是一个

次多项式，推到矛盾。
原命题成立，证毕。

如果我们按照定义求一个多项式的点值表示，时间复杂度为

已知多项式的点值表示，求其系数表示，可以使用插值。朴素的插值算法时间复杂度为

。

关于多项式的乘法

已知在一组插值节点

中

(假设个多项式的项数相同，没有的视为

) 的点值向量分别为

，那么

的点值表达式可以在

的时间内求出，为

。

因为

的项数为

的项数之和。

设

分别有

项所以我们带入的插值节点有至少有

个。

如果我们能快速通过点值表式求出系数表示，那么就搭起了它们之间的一座桥了。

这也是快速傅里叶变换的基本思路，由系数表达式到点值表达式到结果的点值表达式再到结果的系数表达式。

0x02 关于复数的基本了解

我们把形如

这样的数叫做复数，复数集合用

来表示。其中

称为实部

，

称为虚部

为虚数单位，指满足

的一个解

；此外，对于这样对复数开偶次幂的数叫做虚数

每一个复数

都对应了一个平面上的向量

我们把这样的平面称为复平面

，它是由水平的实轴与垂直的虚轴建立起来的复数的几何表示。

故每一个复数唯一对应了一个复平面上的向量，每一个复平面上的向量也唯一对应了一个复数。其中

既被认为是实数，也被认为是虚数。

其中复数

的模长

定义为

在复平面的距离到原点的距离，

。幅角

为实轴的正半轴正方向（逆时针）旋转到

的有向角度。

由于虚数无法比较大小。复数之间的大小关系只存在等于与不等于两种关系，两个复数相等当且仅当实部虚部对应相等。对于虚部为

的复数之间是可以比较大小的，相当于实数之间的比较。

复数之间的运算满足结合律，交换律和分配律。

由此定义复数之间的运算法则：

复数运算的加法满足平行四边形法则，乘法满足幅角相加，模长相乘。

对于一个复数

, 它的共轭复数是

称为

的复共轭

共轭复数有一些性质

0x03 复数中的单位根

复平面中的单位圆

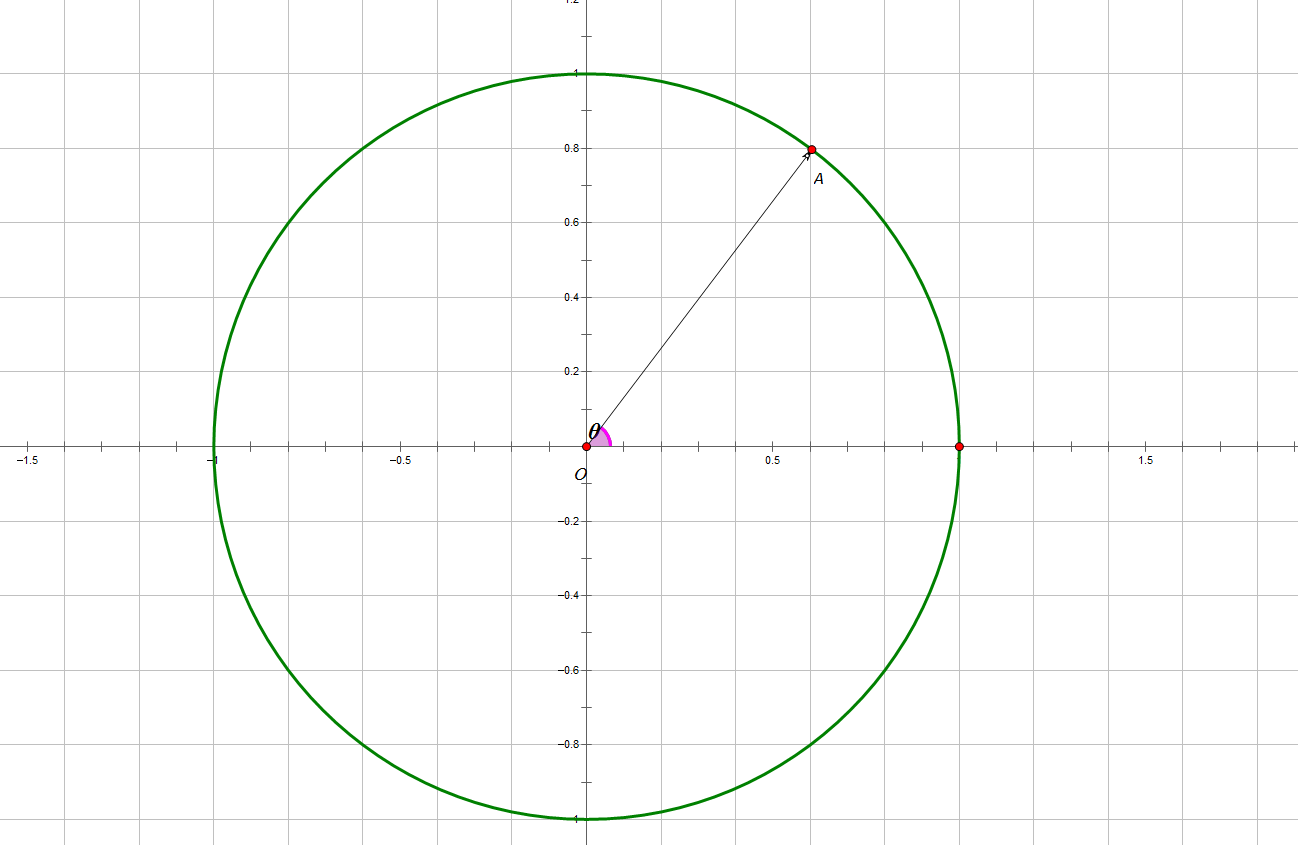
其中

单位根，表示为

，可知

（顺便一提著名的欧拉幅角公式

其实是由定义来的...）

将单位圆等分成

个部分（以单位圆与实轴正半轴的交点一个等分点），以原点为起点，圆的这

个

等分点为终点，作出

个向量。

其中幅角为正且最小的向量称为

次单位向量，记为

。

（有没有大佬帮我补张图啊，画不来）

其余的

个向量分别为

，它们可以由复数之间的乘法得来

。

容易看出

。

对于

, 它事实上就是

。

所以

关于单位根有两个性质

性质一（又称为折半引理）：

证明一：

由几何意义，这两者表示的向量终点是一样的。

证明二：

由计算的公式：

其实由此我们可以引申出

性质二（又称为消去引理）

证明一：

由几何意义，这两者表示的向量终点是相反的，左边较右边在单位圆上多转了半圈。

证明二：

由计算的公式：

最后一步由三角恒等变换得到。

0x04 离散傅里叶变换（Discrete Fourier Transform）

首先我们单独考虑一个

项（

）的多项式

，其系数向量为

。我们将

次单位根的

次幂分别带入

得到其点值向量

。

这个过程称为离散傅里叶变换（Discrete Fourier Transform）。

如果朴素带入，时间复杂度也是

的。

所以我们必须要利用到单位根

的特殊性质。

对于

考虑将其按照奇偶分组

令

则可得到

分类讨论

设

，

由上文提到的折半引理

对于

其中

由消去引理

故

注意，

与

取遍了

中的

个整数，保证了可以由这

个点值反推解出系数（上文已证明）。

于是我们可以知道

如果已知了

分别在

的取值，可以在

的时间内求出

的取值。

而

都是

一半的规模，显然可以转化为子问题递归求解。

时间复杂度：

0x05 离散傅里叶反变换（Inverse Discrete Fourier Transform）

使用快速傅里叶变换将点值表示的多项式转化为系数表示，这个过程叫做离散傅里叶反变换（Inverse Discrete Fourier Transform）。

即由

维点值向量

推出

维系数向量

。

设

为

得到的离散傅里叶变换的结果。

我们构造一个多项式

设向量

中

为

在

的点值表示

即

，

我们考虑对

进行还原

于是

由和式的性质

令

对其进行化简

设

则

其公比为

当

即

时

此时

当

即

时

由等比数列求和公式

, 此时

所以

将

带入原式

所以

其中

为原多项式

的系数向量

中的

由此得到：

对于多项式

由插值节点

做离散傅里叶变换得到的点值向量

。我们将

作为插值节点，

作为系数向量，做一次离散傅里叶变换得到的向量每一项都除以

之后得到的

就是多项式的系数向量

。

注意到

是

的共轭复数。

这个过程称为离散傅里叶反变换。

0x06 关于 FFT 在 C++ 的实现

首先要解决复数运算的问题，我们可以使用 C++STL 自带的

依照精度要求

一般为

。

也可以自己封装，下面是我封装的复数类。

struct Complex  {
	double r, i ;
	Complex ( )  {	}
	Complex ( double r, double i ) : r ( r ), i ( i )  {	}
	inline void real ( const double& x )  {  r = x ;  }
	inline double real ( )  {  return r ;  }
	inline Complex operator + ( const Complex& rhs )  const  {
		return Complex ( r + rhs.r, i + rhs.i ) ;
	}
	inline Complex operator - ( const Complex& rhs )  const  {
		return Complex ( r - rhs.r, i - rhs.i ) ;
	}
	inline Complex operator * ( const Complex& rhs )  const  {
		return Complex ( r * rhs.r - i * rhs.i, r * rhs.i + i * rhs.r ) ;
	}
	inline void operator /= ( const double& x )   {
		r /= x, i /= x ;
	}
	inline void operator *= ( const Complex& rhs )   {
		*this = Complex ( r * rhs.r - i * rhs.i, r * rhs.i + i * rhs.r ) ;
	}
	inline void operator += ( const Complex& rhs )   {
		r += rhs.r, i += rhs.i ;
	}
	inline Complex conj ( )  {
		return Complex ( r, -i ) ;
	}
} ;

我们由上面的分析可以得到这个递归的写法。

bool inverse = false ;

inline Complex omega ( const int& n, const int& k )  {
    if ( ! inverse ) return Complex ( cos ( 2 * PI / n * k ), sin ( 2 * PI / n * k ) ) ;
    return Complex ( cos ( 2 * PI / n * k ), sin ( 2 * PI / n * k ) ).conj ( ) ;
}

inline void fft ( Complex *a, const int& n )  {
    if ( n == 1 ) return ;

    static Complex buf [N] ;
    
    const int m = n >> 1 ;
    
    for ( int i = 0 ; i < m ; ++ i )  {
        buf [i] = a [i << 1] ;
        buf [i + m] = a [i << 1 | 1] ;
    }
    
    memcpy ( a, buf, sizeof ( Complex ) * ( n + 1 ) ) ;

    Complex *a1 = a, *a2 = a + m;
    fft ( a1, m ) ;
    fft ( a2, m ) ;

    for ( int i = 0 ; i < m ; ++ i )  {
        Complex t = omega ( n, i ) ;
        buf [i] = a1 [i] + t * a2 [i] ;
        buf [i + m] = a1 [i] - t * a2 [i] ;
    }
    
    memcpy ( a, buf, sizeof ( Complex ) * ( n + 1 ) ) ;
}

但是这样的

要用到辅助数组，并且常数比较大。

能不能优化呢？

我们把每一次分组的情况推演出来

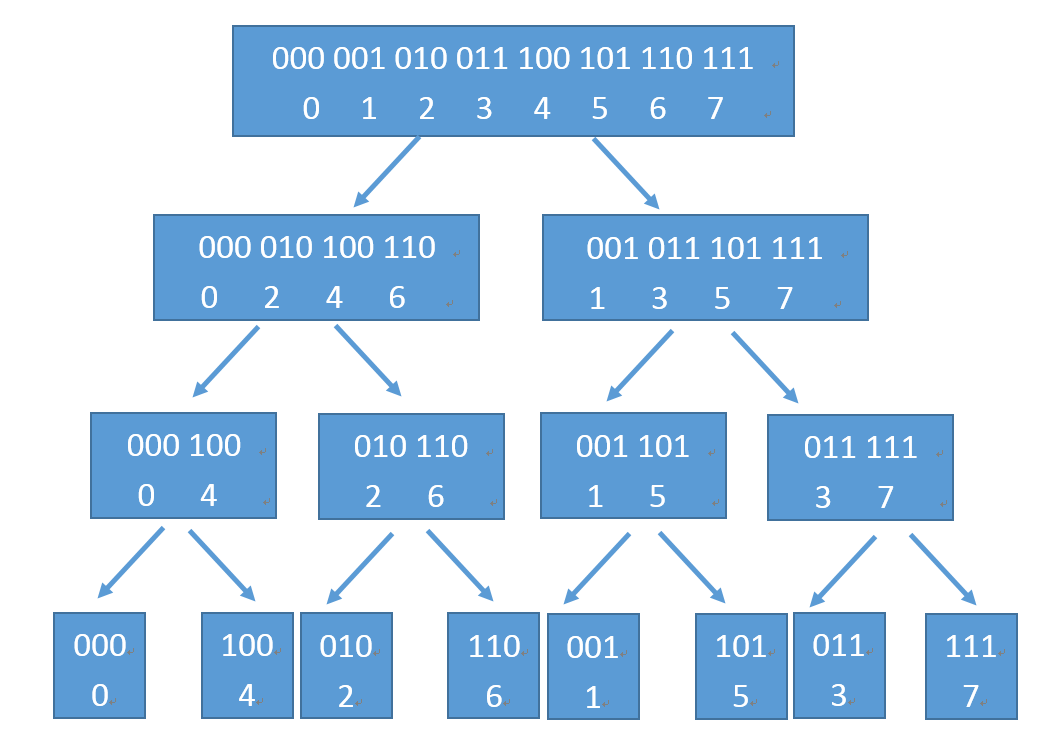
递归分类的每一层

观察到每一个位置的数其实都是原来位置上的数的二进制后

位

了一下。

于是我们可以想，先将原数组调整成最底层的位置（很好调整吧）。

然后从倒数第二层由底向上计算。

这就是我们一般用来实现

的

算法。

考虑怎么合并？

在

算法中，合并操作被称作是蝴蝶操作。

虑合并两个子问题的过程，这一层有

项需要处理。假设

和

分别存在

和

中，

和

将要被存放在

和

中，合并的单位操作可表示为

只要将合并顺序换一下，再加入一个临时变量，合并过程就可以在原数组中进行。

令

合并过程如下：

。

至此，我们可以给出

算法的实现。

struct FastFourierTransform  {
    Complex omega [N], omegaInverse [N] ;

    void init ( const int& n )  {
        for ( int i = 0 ; i < n ; ++ i )  {
            omega [i] = Complex ( cos ( 2 * PI / n * i), sin ( 2 * PI / n * i ) ) ;
            omegaInverse [i] = omega [i].conj ( ) ;
        }
    }

    void transform ( Complex *a, const int& n, const Complex* omega ) {
        for ( int i = 0, j = 0 ; i < n ; ++ i )  {
		if ( i > j )  std :: swap ( a [i], a [j] ) ;
		for( int l = n >> 1 ; ( j ^= l ) < l ; l >>= 1 ) ;
	}

        for ( int l = 2 ; l <= n ; l <<= 1 )  {
            int m = l / 2;
            for ( Complex *p = a ; p != a + n ; p += l )  {
                for ( int i = 0 ; i < m ; ++ i )  {
                    Complex t = omega [n / l * i] * p [m + i] ;
                    p [m + i] = p [i] - t ;
                    p [i] += t ;
                }
            }
        }
    }

    void dft ( Complex *a, const int& n )  {
        transform ( a, n, omega ) ;
    }

    void idft ( Complex *a, const int& n )  {
        transform ( a, n, omegaInverse ) ;
        for ( int i = 0 ; i < n ; ++ i ) a [i] /= n ;
    }
} fft ;

注意代码中的